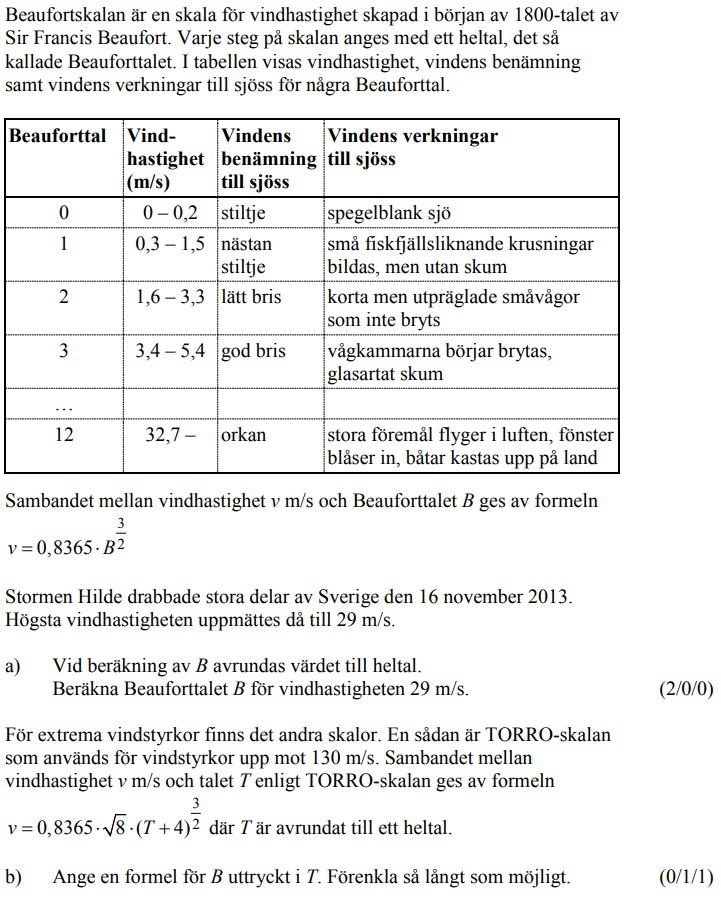
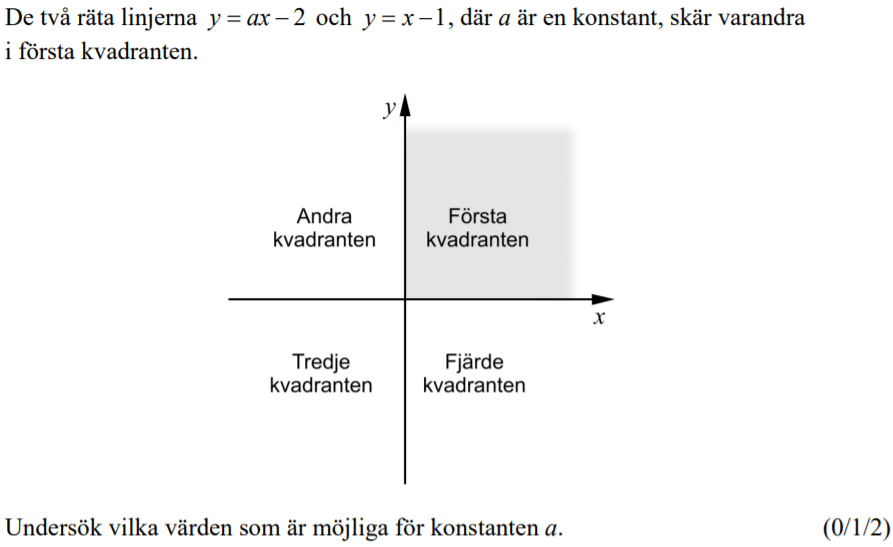
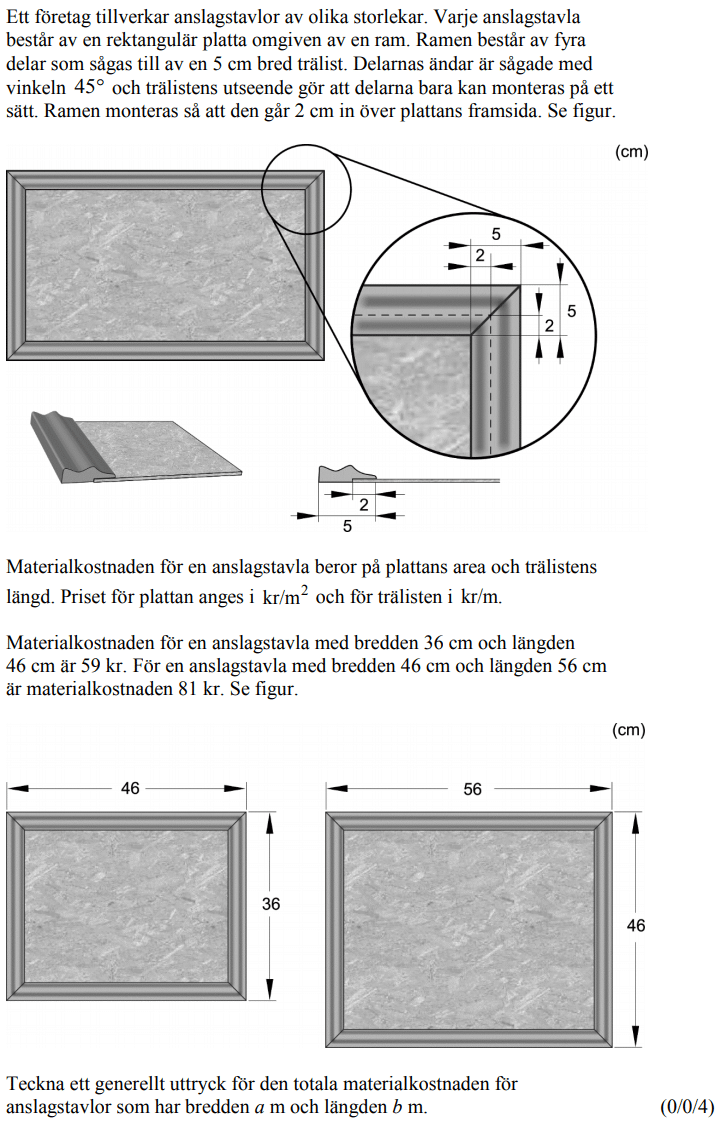
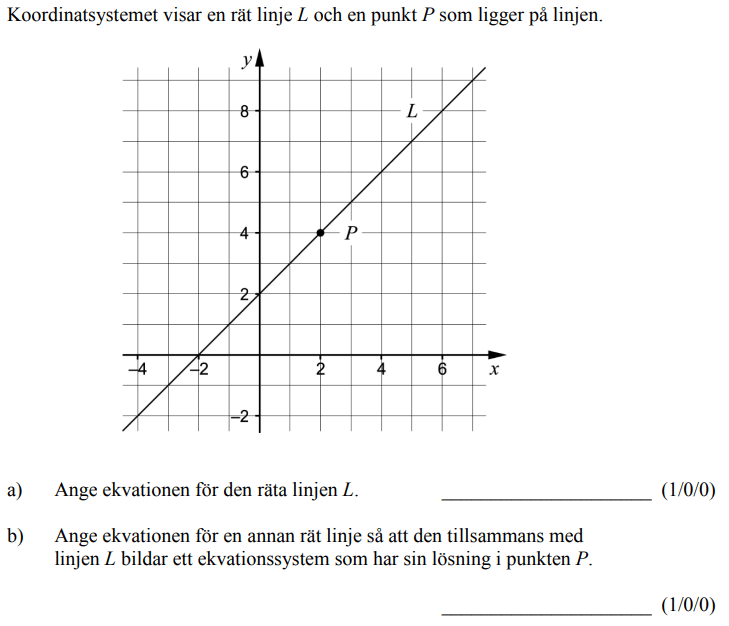
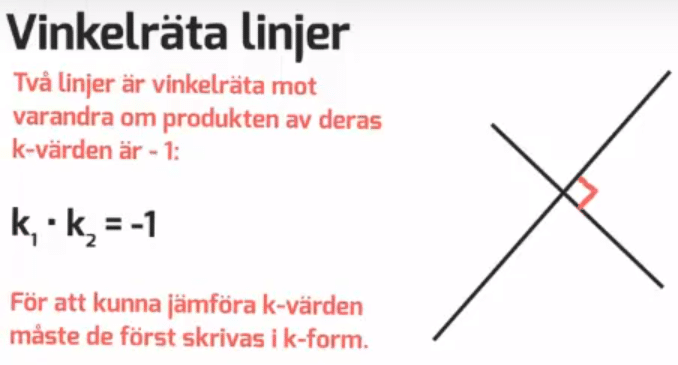
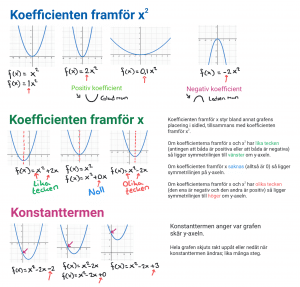
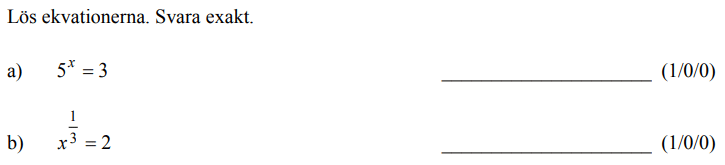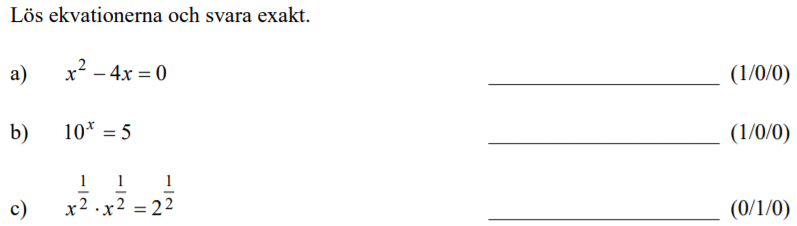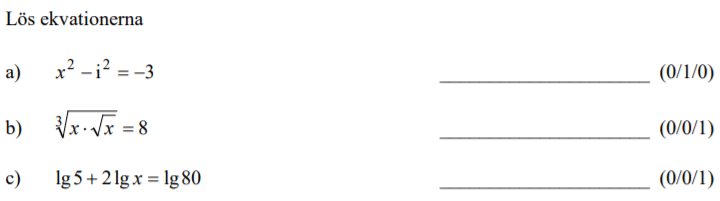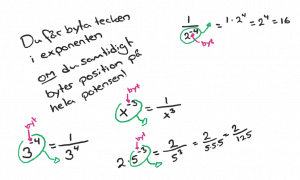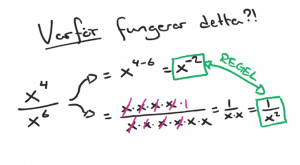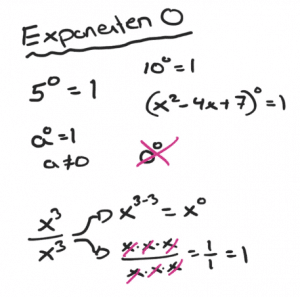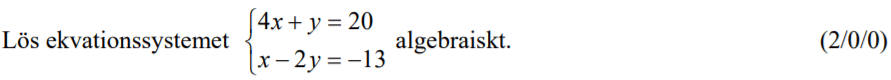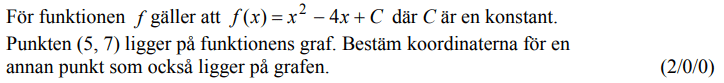Randvinkelsatsen med följdsatser 1
Genomgångar:
Randvinkelsatsen, med följdsatser. Även förklaringar om varför följdsatserna fungerar.
Mer kortfattad genomgång: Randvinkelsatsen, med följdsatser.
Randvinkelsatsen
Bevis för randvinkelsatsen
Bevis för randvinkelsatsen
Yttervinkelsatsen, samt bevis av randvinkelsatsen med hjälp av denna.
Testa själv:
Randvinkelsatsen
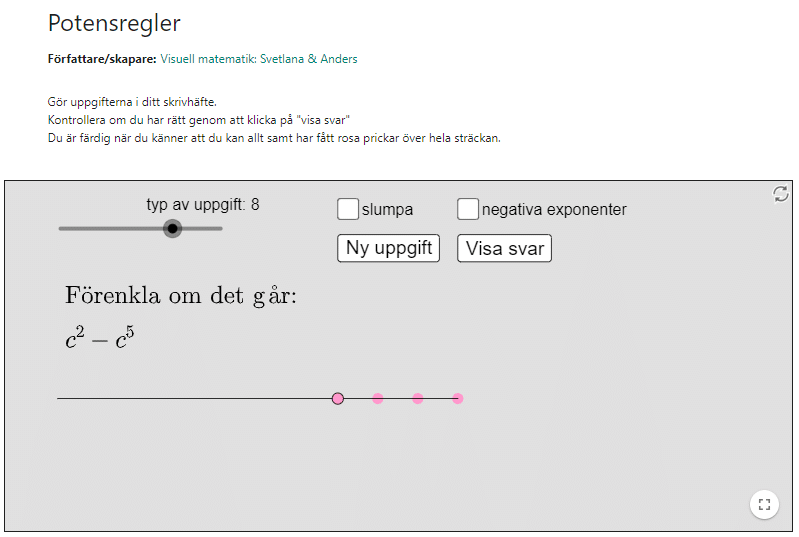
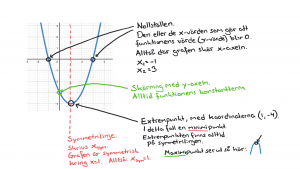
Regel:
En medelpunktsvinkel är alltid dubbelt så stor som en randvinkel.
Dra i punkterna nedan så ser du!
Följdsatser till randvinkelsatsen
Regel:
Alla randvinklar som utgår från en och samma cirkelbåge är alltid lika stora.
Dra i punkterna nedan så ser du!
Regel:
Randvinklar till en halvcirkelbåge är räta vinklar.
Dra i punkterna nedan så ser du!
Regel:
I en fyrhörning som är inskriven i en cirkel är motstående vinklar tillsammans 180 grader.
Dra i punkterna nedan så ser du!
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till den.

Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
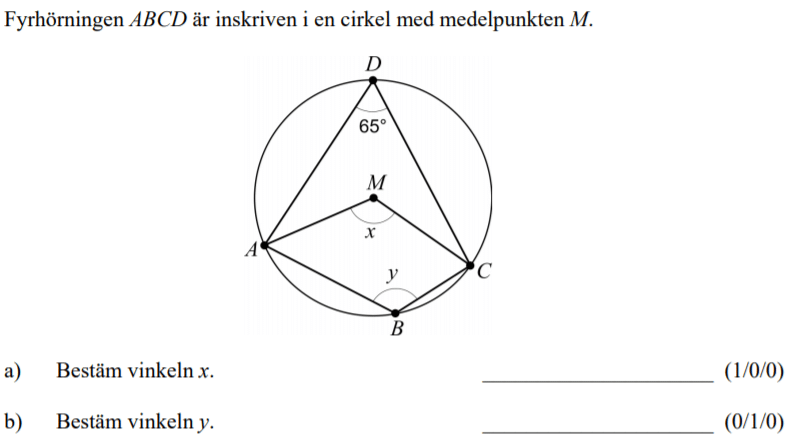
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
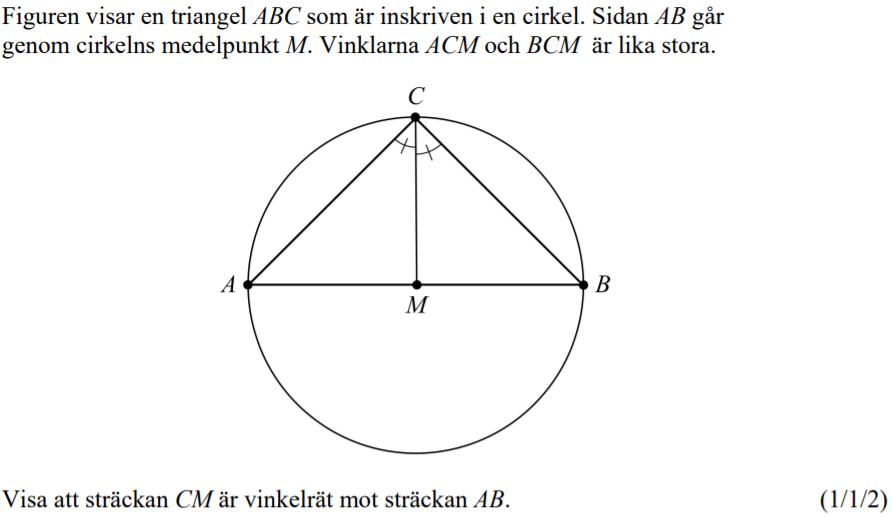
Från HT 2012 (Matematik 2a, 2b eller 2c).