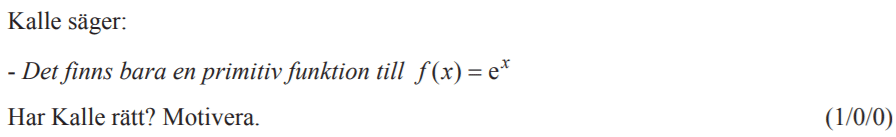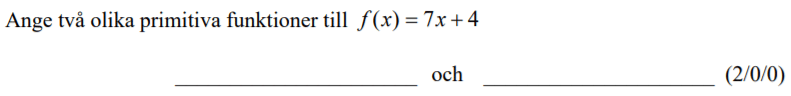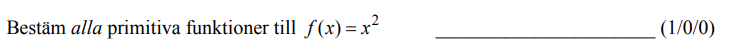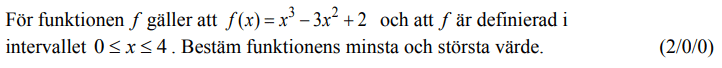Geometrisk talföljd och geometrisk summa
Geometrisk talföljd och geometrisk summa
Geonomgång om geometriska talföljder och geometrisk summa
Två tillämpningsuppgifter
Geometrisk summa och ekonomisk tillämpningsuppgift
En genomgång som fokuserar på lite enklare uppgifter:



Nuvärde
Annuitetslån
Genomgång om lån med rak amortering och annuitetslån.
Liknande genomgång
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till den!
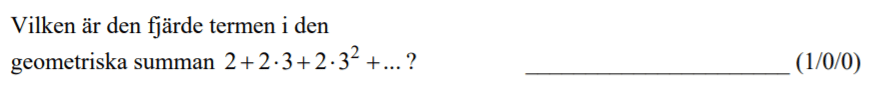
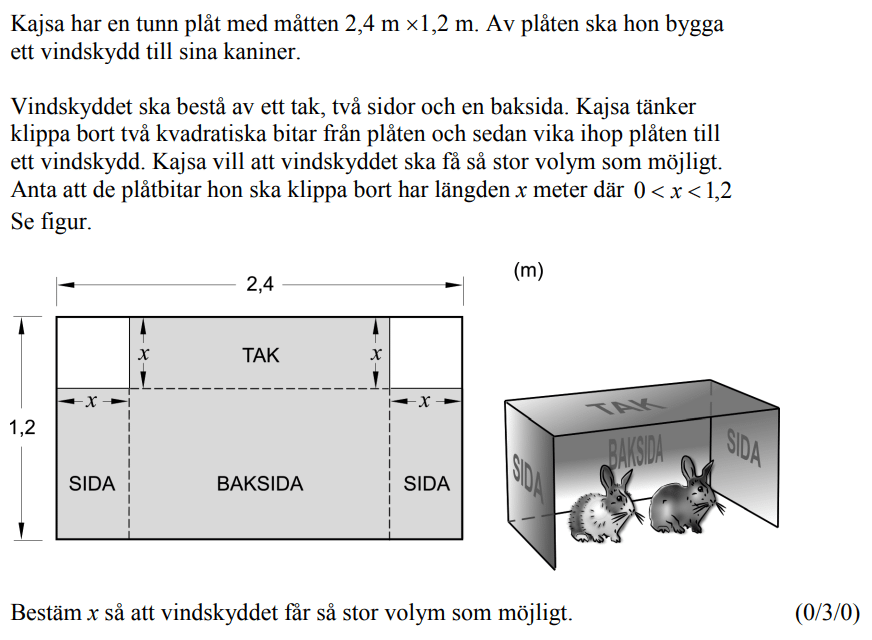
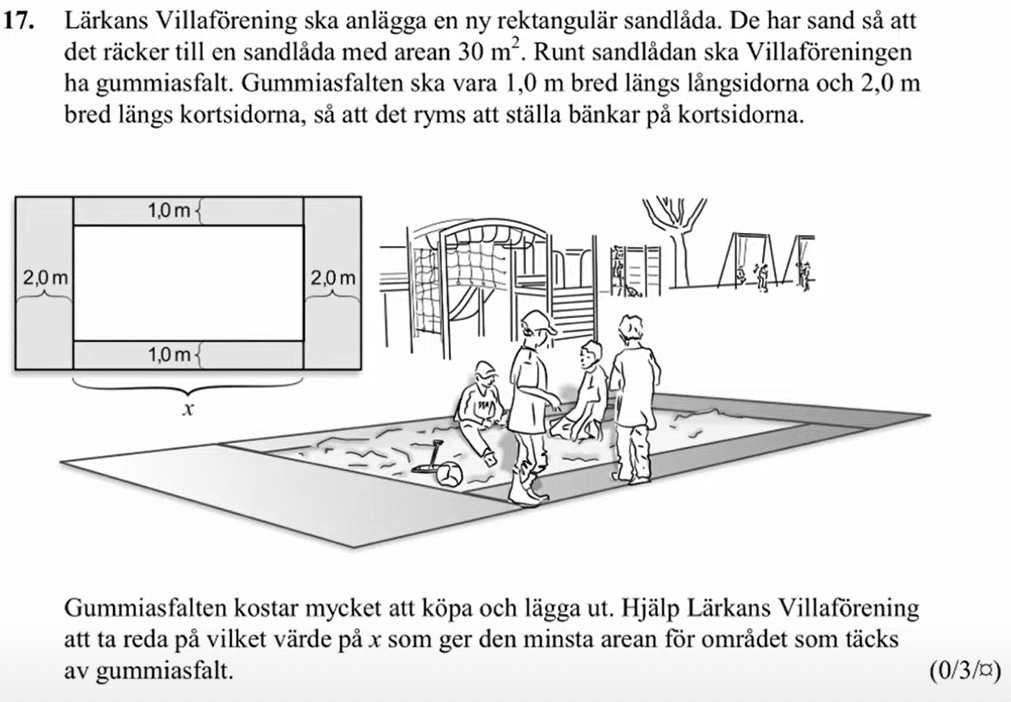
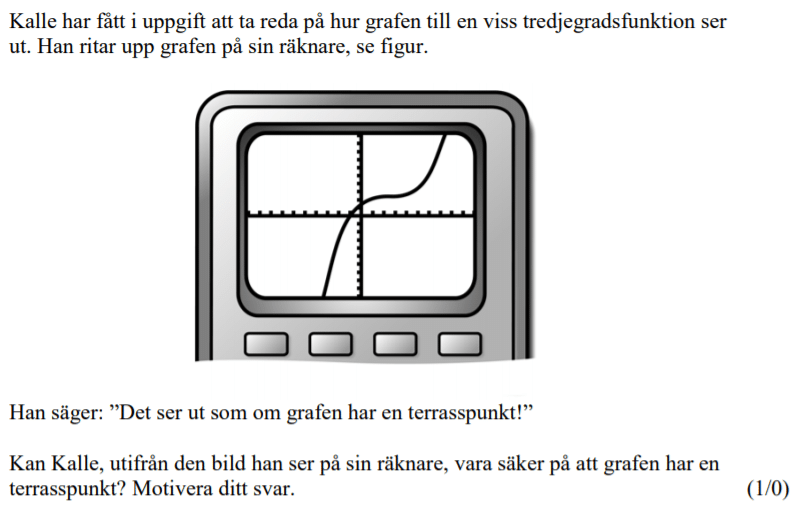
Från HT 2012 (Matematik 3b).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
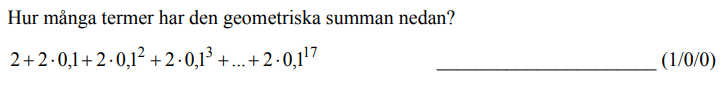
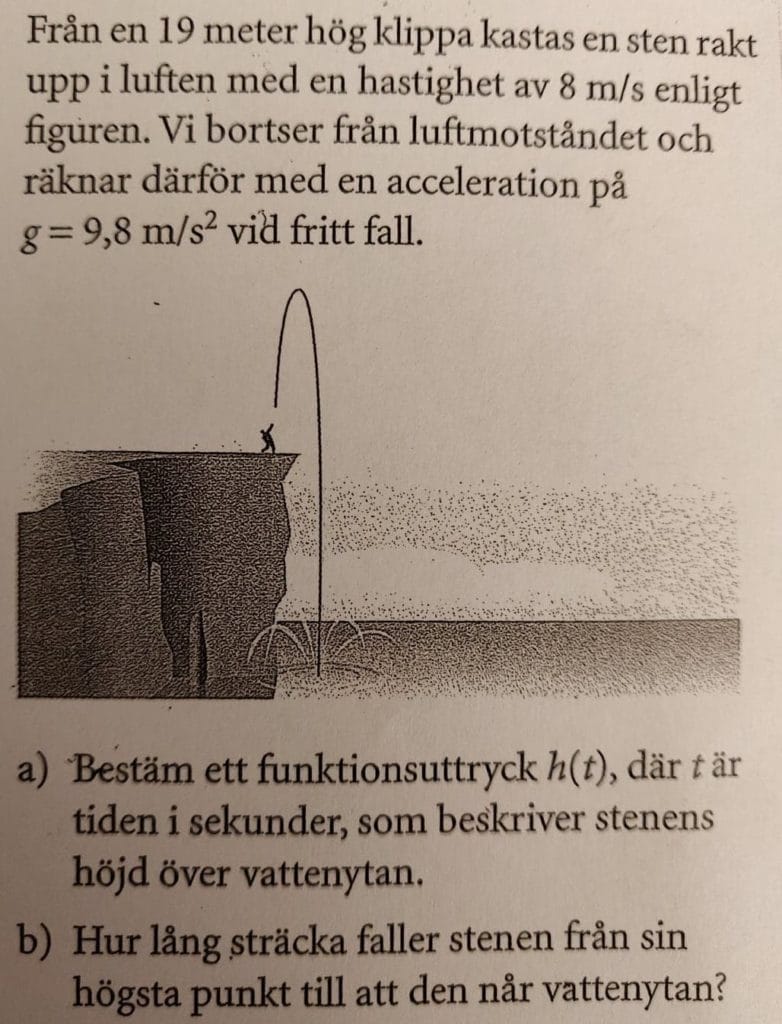
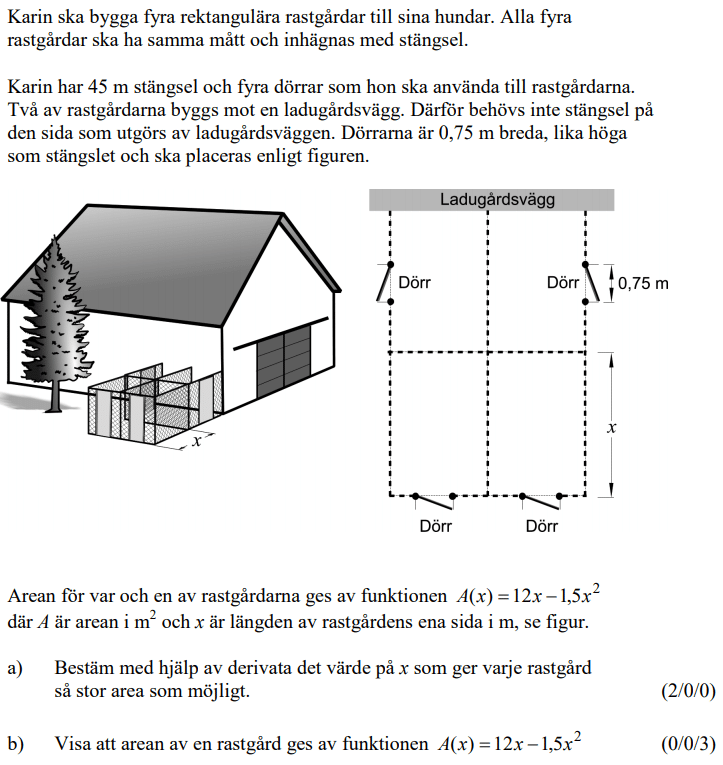
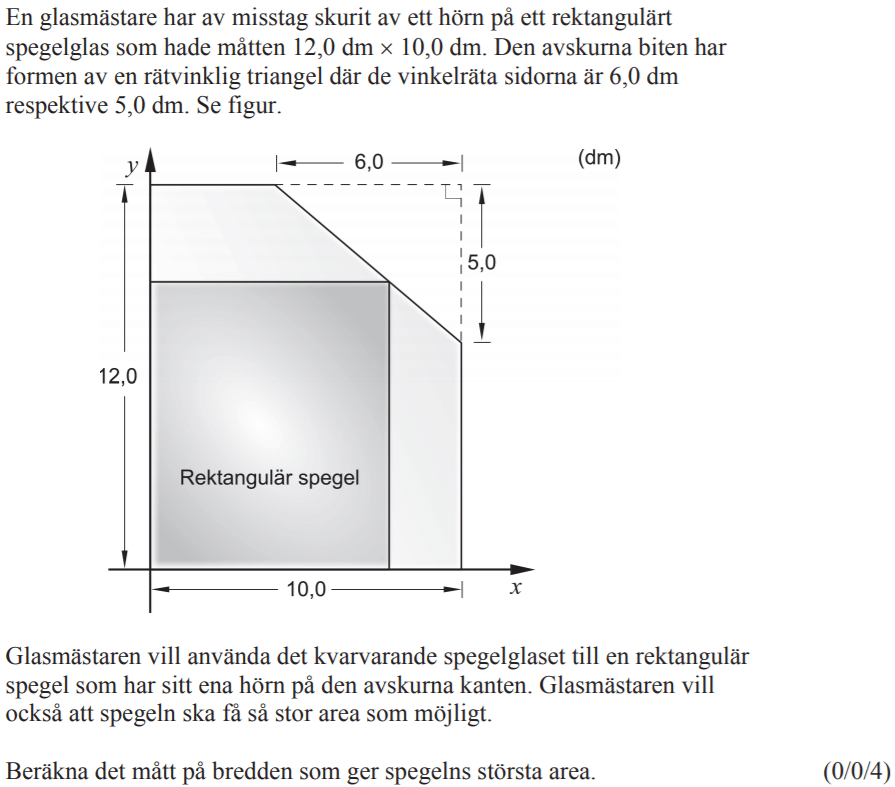
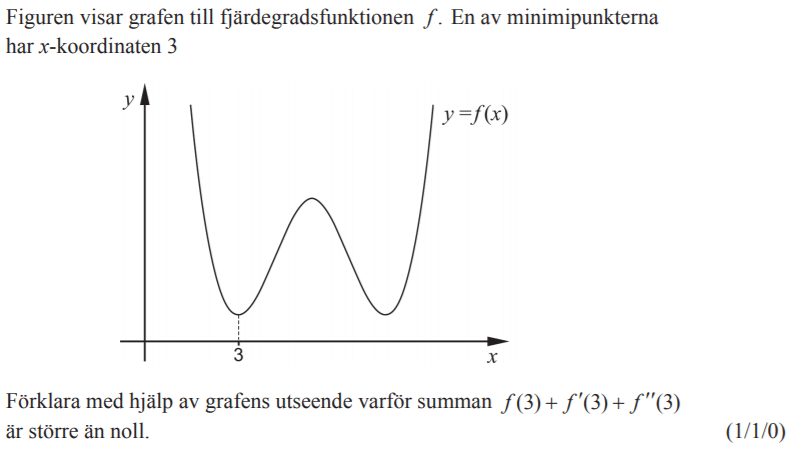
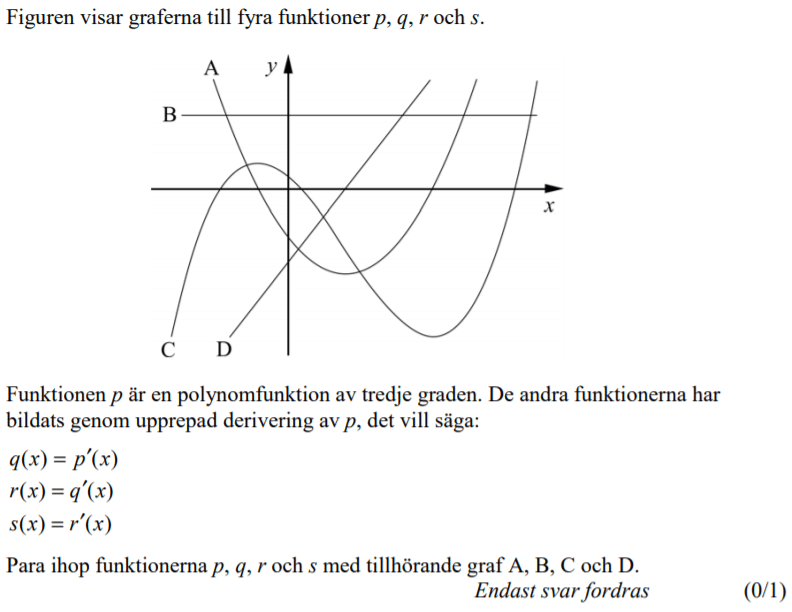
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b)

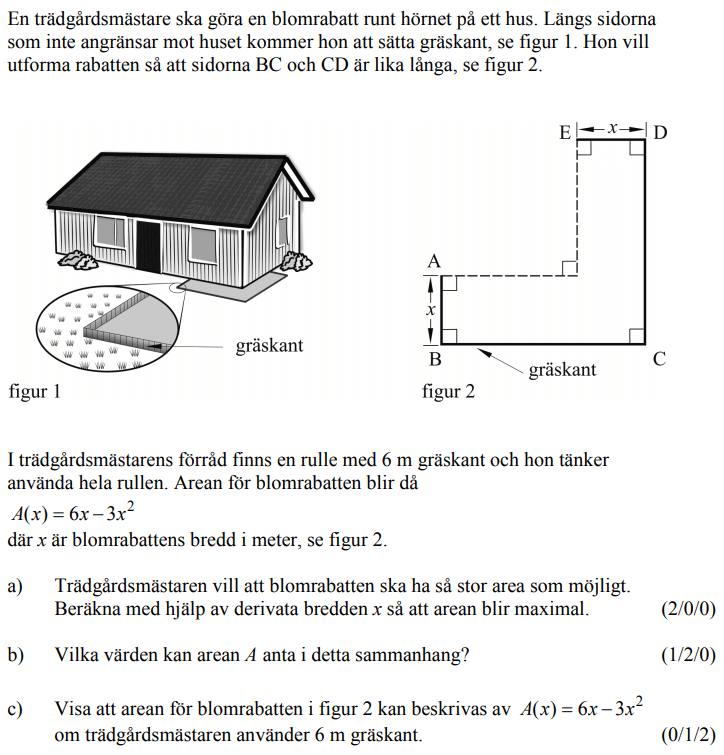
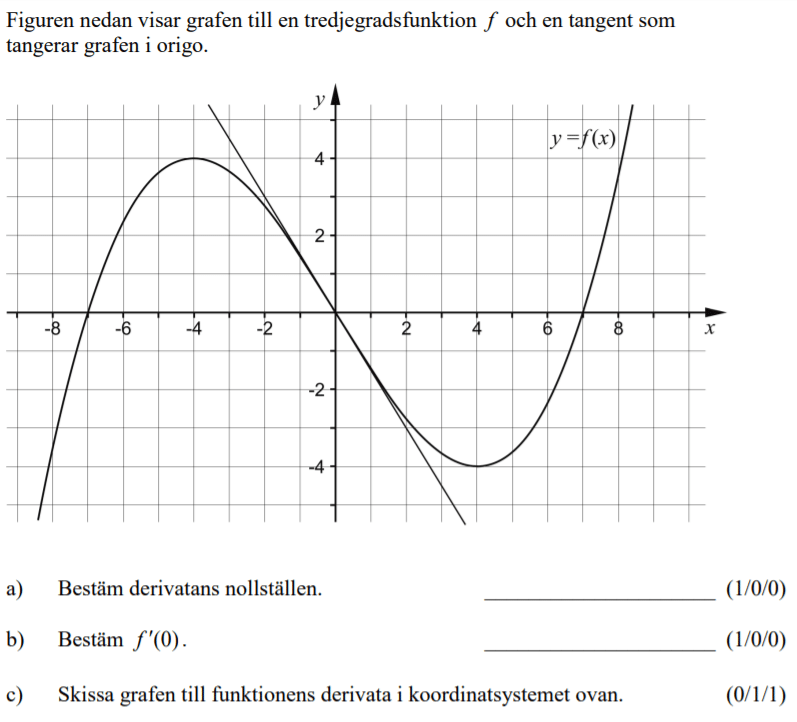
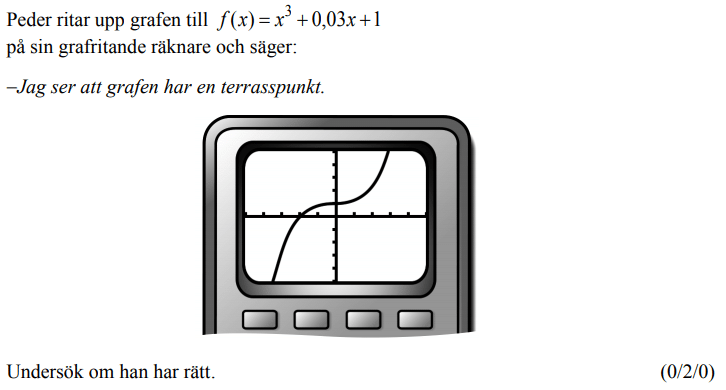
Från HT 2012 (Matematik 3b).
Videoförklaringen är gjord av min tidigare kollega David Johansson.

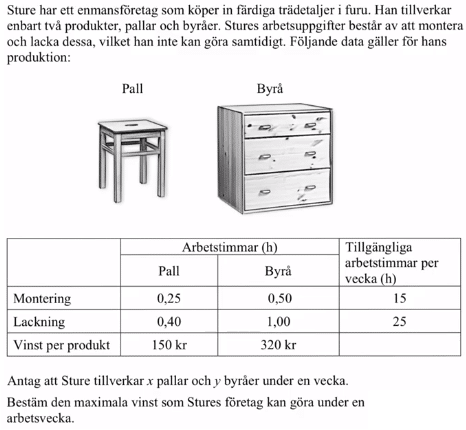
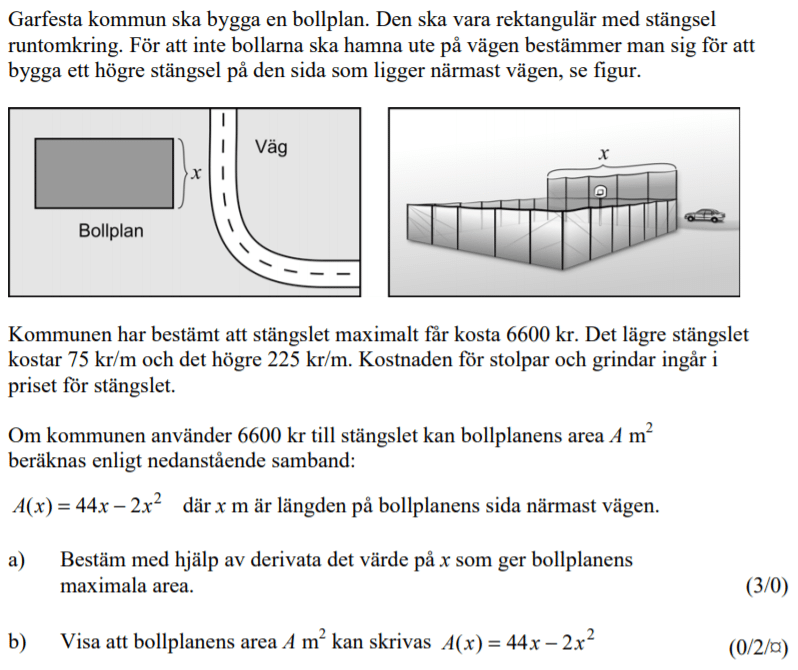
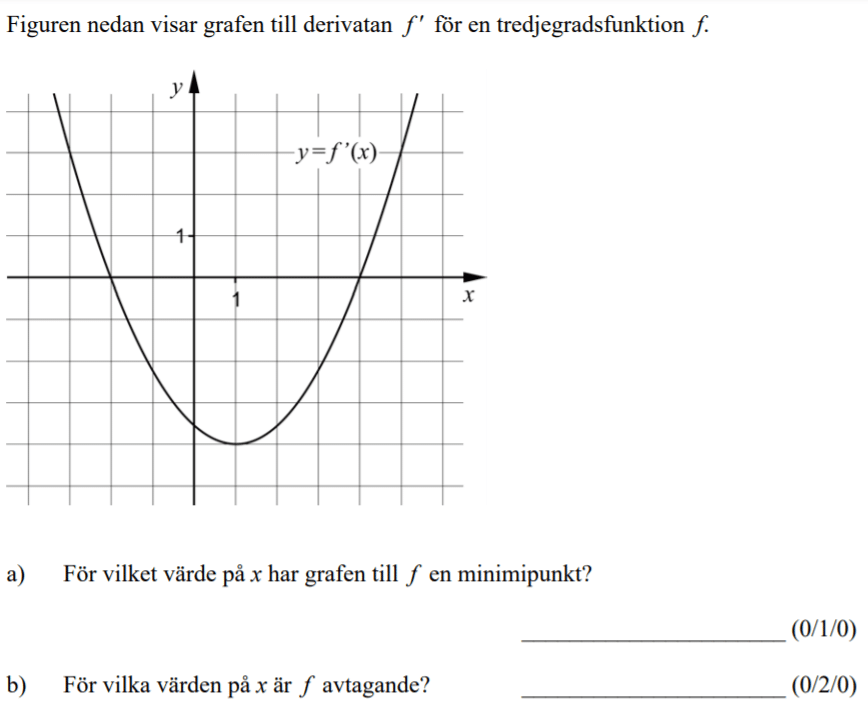
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.

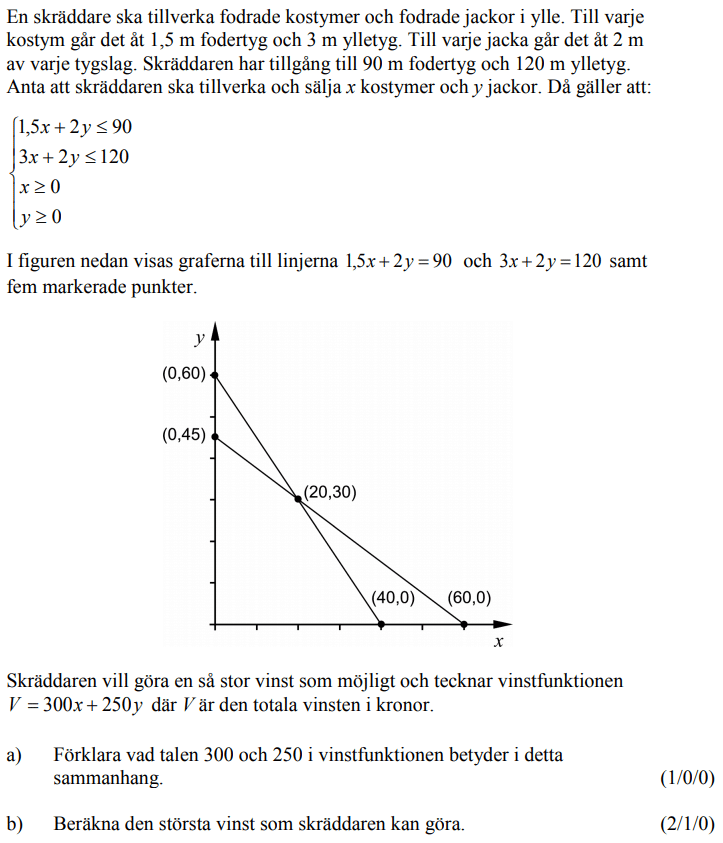
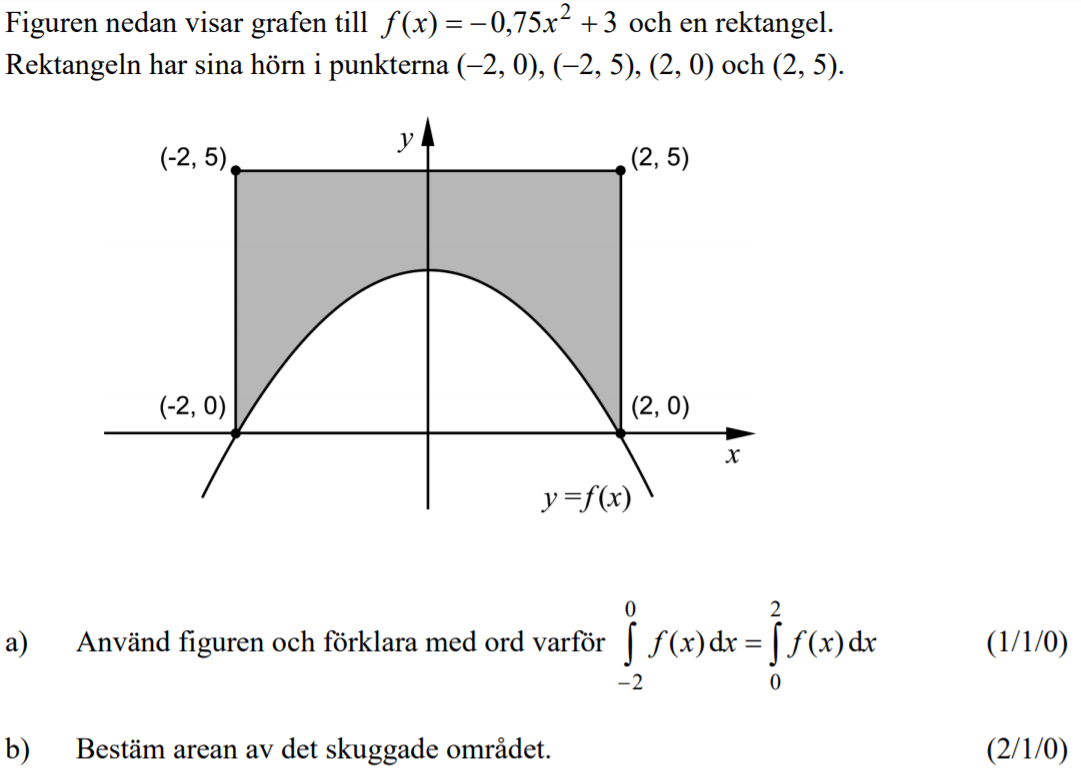
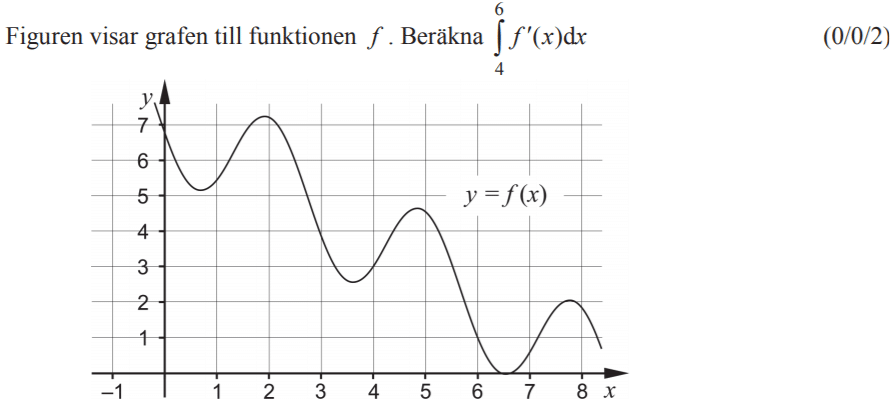
Från HT 2013 (Matematik 3b)

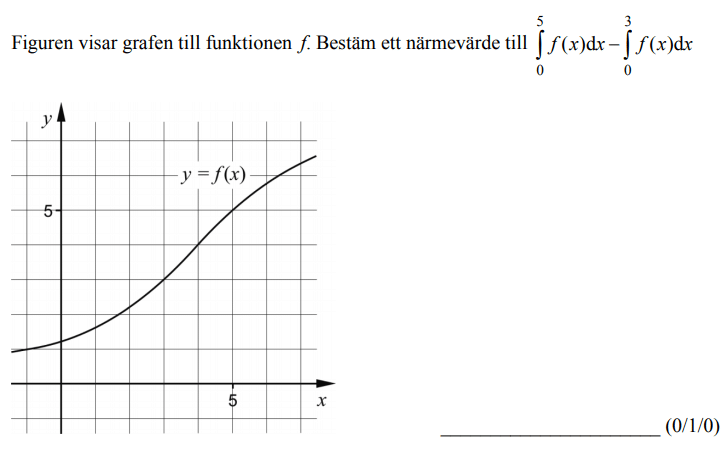
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b)

Från VT 2013 (Matematik 3b)