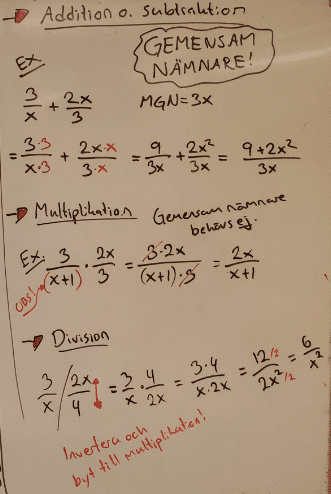Förenkling av rationella uttryck
Hur du förenklar ett rationellt uttryck:
För att förkorta ett rationellt uttryck behöver du först faktorisera:
1. Bryt ut.
Bryt ut gemensam faktor om det går.
2. Regel baklänges.
Går det att använda kvadreringsreglerna eller konjugatregeln baklänges?
3. pq-formeln.
Faktorisera med hjälp av pq-formeln. Alltså beräkna nollställena x1 och x2 och skriv sedan på formen (x-x1)(x-x2).
4. Bryta ut ett negativt tal.
Hjälper det att bryta ut ett negativt tal, exempelvis (-1) ? Detta gör att tecknen i parentesen byts och att exempelvis (5-x) kan skrivas om till -1(x-5).
Förenkla rationella uttryck: tydlig genomgång
Liknande genomgång
Svårare uppgifter där vi behöver bryta ut negativa tal
Liknande genomgång
Sammanfattande bilder:
Förkorta rationella uttryck
Observera att du bara kan förkorta bort faktorer, som alltså sitter med multiplikation.

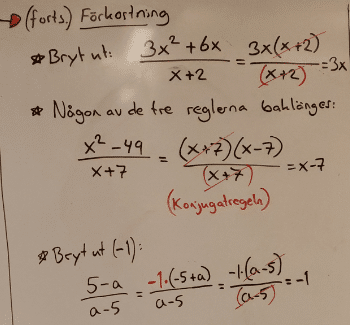
Förlänga rationella uttryck
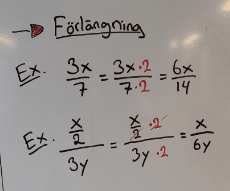
Ytterligare liknande genomgångar:
Förenkla rationella uttryck (förlänga och förkorta)
Introduktion:
När får man förkorta och när får man inte det?
Förenkla rationella uttryck
TYDLIGT EXEMPEL: Att förenkla ett rationellt uttryck genom att faktorisera täljare och nämnare
Ett något svårare exempel, men mycket tydligt.
Ibland hjälper det att bryta ut (-1).
Genom att bryta ut (-1) kan du få termerna att byta tecken:
x-7 = -1(-x+7) = -1(7-x).
Ibland kan detta hjälpa, om vi exempelvis har x-7 i täljaren och 7-x i nämnaren.
Klippet startar en bit in i genomgången.
Uppgifter med videoförklaringar
Klicka på en uppgift för att se en videoförklaring
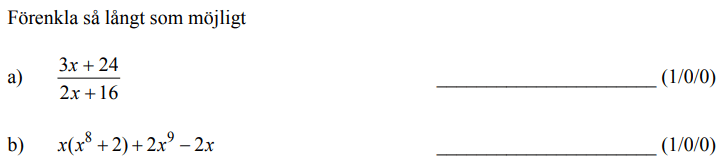
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 2).

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 5).

Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 14).

Löses utan digitala hjälpmedel.
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 6).

Löses utan digitala hjälpmedel.
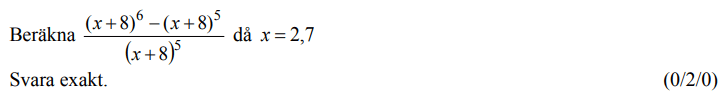
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 14).