Rest, kongruens och moduloräkning
Liknande genomgång: Grunder om kongruens och moduloräkning
Svårare exempel med potenser, två genomgångar
Kongruenstabell
Kongruenstabell kan användas för att visa att ett tal är en delare till ett uttryck.
Anders Karlsson lär mig och tittarna på livesändningen 2022 hur det fungerar med kongruenstabell.

Liknande tidigare genomgångar
Modulo och kongruens (ej räkneregler)
Räkneregler för kongruens
OBS: På formelbladet ser reglerna annorlunda ut än i genomgången, se bild längre ner:
Formelbladet:
(Det finns numera inget officiellt formelblad för Matematik 5 sedan Skolverket gjorde om kursen inför läsår 2021-2022. De flesta lärare låter dock eleverna ha ett formelblad där detta står med, men det är inte helt säkert att det står precis så här. Så här såg det gamla formelbladet ut).
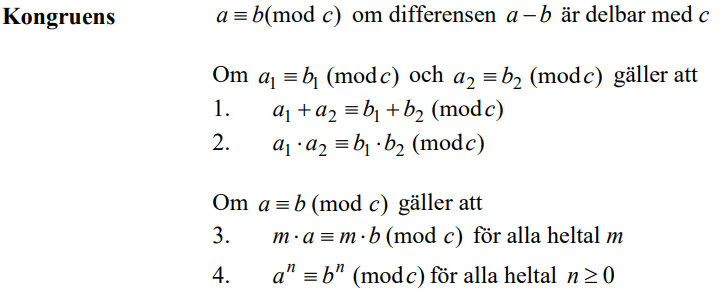

Bestäm alla heltal x som uppfyller kongruensekvationer
det finns 3 olika uppgifter a,b och c
jag tar denna:
x^2 är kongruent med 1 (mod 8)
Hur ska jag tänka på en sådan uppgift eller hur ska den lösas.
Hej Jonas, längst ner skriver du att det inte finns något officielt formelblad. Betyder detta att olika skolor använder olika formelblad, trots att de flesta skolor använder samma kursprov? Eller använder olika skolor oftast helt egna kursprov?
Hej!
Ja, varje lärare/skola får själva bestämma hur de lägger upp kursen och vilka kursprov de väljer att göra, samt vad eleverna får ha tillgång till. Skolverket har inget kursprov, så skolorna får ordna med det själva på ett eller annat sätt (ibland kan skolor gå ihop och sätta ihop ett prov tillsammans exempelvis). De väljer också vad eleverna ska ha tillgång till för formelblad.
Det viktigaste är att kursen täcker kursinnehållet på ett bra sätt (centralt innehåll i kursplanen), samt att eleverna får bra möjligheter att visa sina kunskaper för respektive betygssteg.