Regression
Vid en regression eller regressionsanalys förenklas sambandet till en modell eller en funktion. En linjär regression innebär att vi skriver en linjär funktion på formen y = kx + m som så noga som möjligt följer de punkter som lagts ut i koordinatsystemet.
Ex: Efter en undersökning av något (exempelvis volym och vikt för någonting) skulle vi kunna uttrycka oss så här:
”Sambandet mellan volym och vikt visar stark korrelation och regressionen visar att det följer sambandet y = 2x + 3, där x = volym och y = vikt.” Här har jag nu hittat på funktionen, men när man gör en regression så räknar vi fram den utifrån givna värden.
Genomgång: Att göra en regression i GeoGebra
Jag visar hur vi gör en linjär regression på två olika sätt, men också hur vi anpassar en exponentialfunktion eller en andragradsfunktion till punkterna.
Regressionsanalys - när vi också tar reda på korrelationskoefficienten r.
- Vad innebär korrelationskoefficienten?
- Göra regressioner och regressionsanalys i Desmos och GeoGebra
Korrelationskoefficienten r är ett mått på hur stark korrelationen är.
Korrelationskoefficienten r kan anta värden från -1 till 1.
- Om r=1 så ligger alla punkterna samlade på en linje som har positiv lutning. Det är då en mycket stark, positiv korrelation.
- Om r=-1 så ligger alla punkterna samlade på en linje som har negativ lutning. Det är då en mycket stark, negativ korrelation.
- Om r är nära 1 eller -1 så är korrelationen stark.
- Om r är ganska långt ifrån 0, men också långt ifrån 1 eller -1 så är korrelationen svag.
- Om r är nära 0 så är korrelationen mycket svag eller obefintlig.
Exakta gränser finns inte utan är en tolkning från situation till situation om vad som bedöms som stark eller svag.
Stark och positiv korrelation
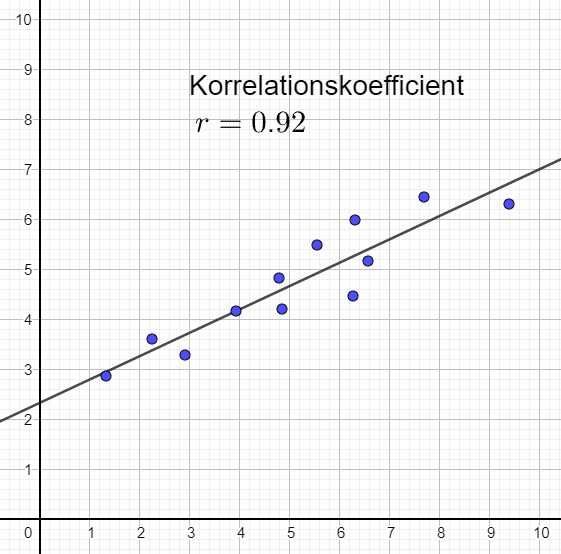
Stark och positiv korrelation
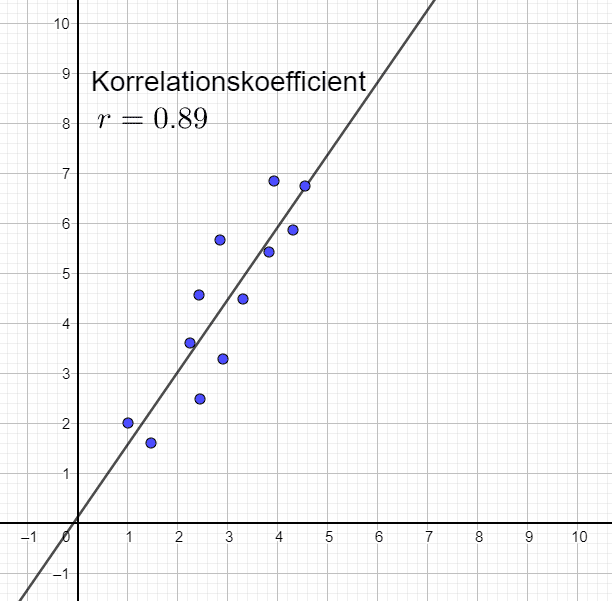
Här lutar linjen brantare än i sambandet till vänster. Hur brant linjen lutar är dock inte avgörande för korrelationskoefficienten r, utan enbart hur väl samlade punkterna är kring linjen, samt om den har positiv eller negativ lutning.
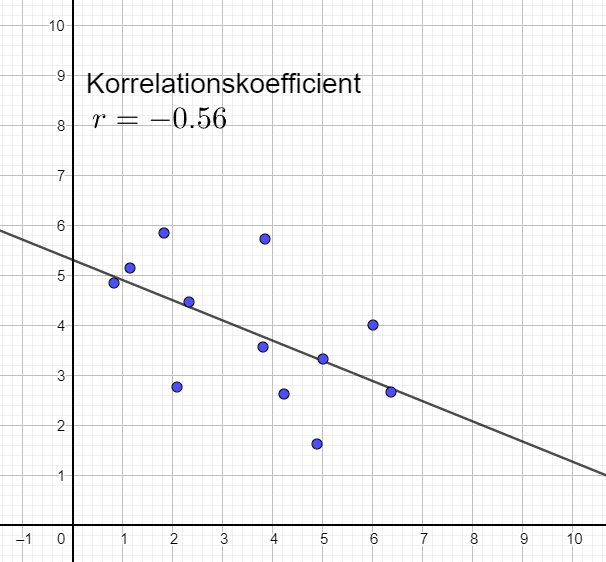
Stark och negativ korrelation
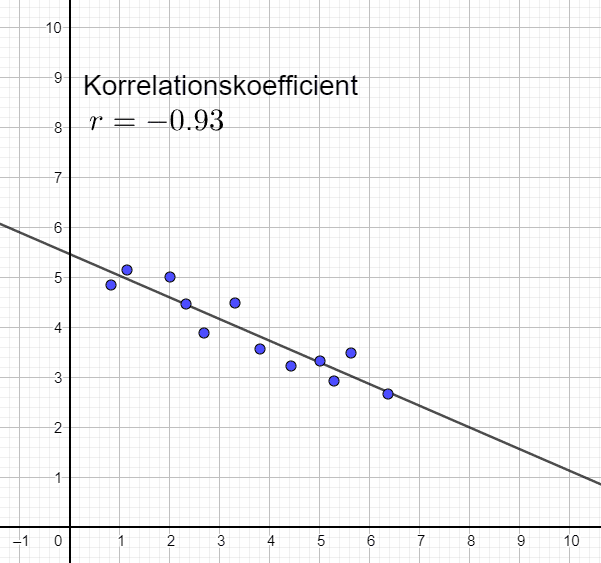
Svag och positiv korrelation
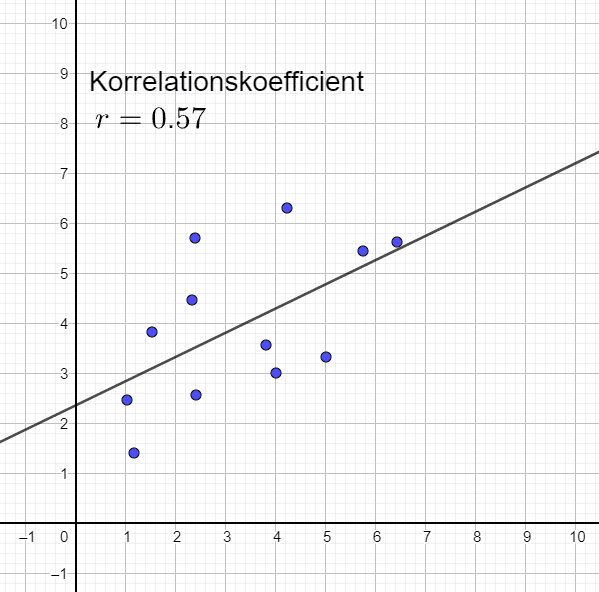
Svag och negativ korrelation
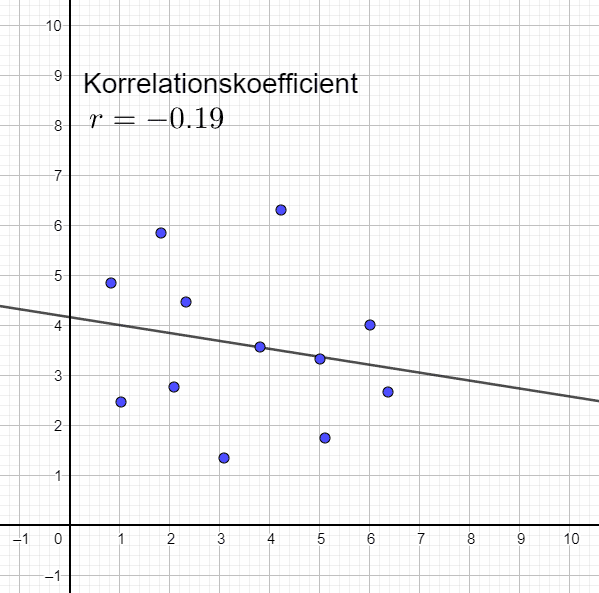
Ingen korrelation (eller ytterst svag och osäker korrelation)
Korrelationskoefficienten visar inte 0, men väldigt nära 0. Eftersom datamängden består av endast ett fåtal punkter är osäkerheten mycket hög. Om endast någon av punkterna skulle ändra position skulle hela linjen kunna förändras från negativ lutning till positiv lutning.
Om vi hade haft många punkter, exempelvis 2000 stycken som visat r=-0,19 så hade vi haft en högre säkerhet och då hade vi kunnat säga att det finns viss korrelation, om än mycket svag sådan.

ge mig ett A jag behövde kolla på hela videon för att förstå och det var jobbigt och tråkigt
Hur gick det? 🙂
Tack för mycket fin inspiration, till både mig och mina elever!
När kan man förvänta sig att hitta en video om linjär regression med GeoGebra?
\\Staffan
Hej igen!
Sorry, jag tittade inte på videon innan jag skrev 😉
Tack!
\\Staffan
Hej Staffan! Det var inte så tydligt att de bitarna ingick i den videon. Tack för kommetaren, ska förtydliga det nu 😀