Tabeller och diagram

Tyvärr saknas en övergripande genomgång.

Frågor från högskoleprovet om tabeller och diagram

Det finns många bra uppgifter att träna på från högskoleprovet våren 2019, som handlar om tabeller och diagram. Jag har spelat in tydliga videoförklaringar till. Gör dessa för att träna!

Provet:

https://www.studera.nu/globalassets/hogskoleprovet/hp-2019-04-06/provpass-2-kvant.pdf

Scrolla ner till fråga 29, där börjar frågorna om tabeller och diagram.

Videoförklaringar till delen om tabeller och diagram:

Uppgifter från tidigare nationella prov för åk 9 och Matematik 1:

Klicka på en uppgift för att se en videoförklaring till denna.

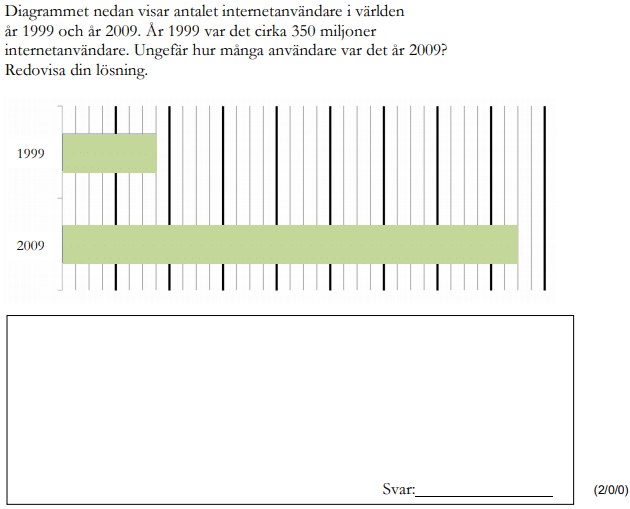
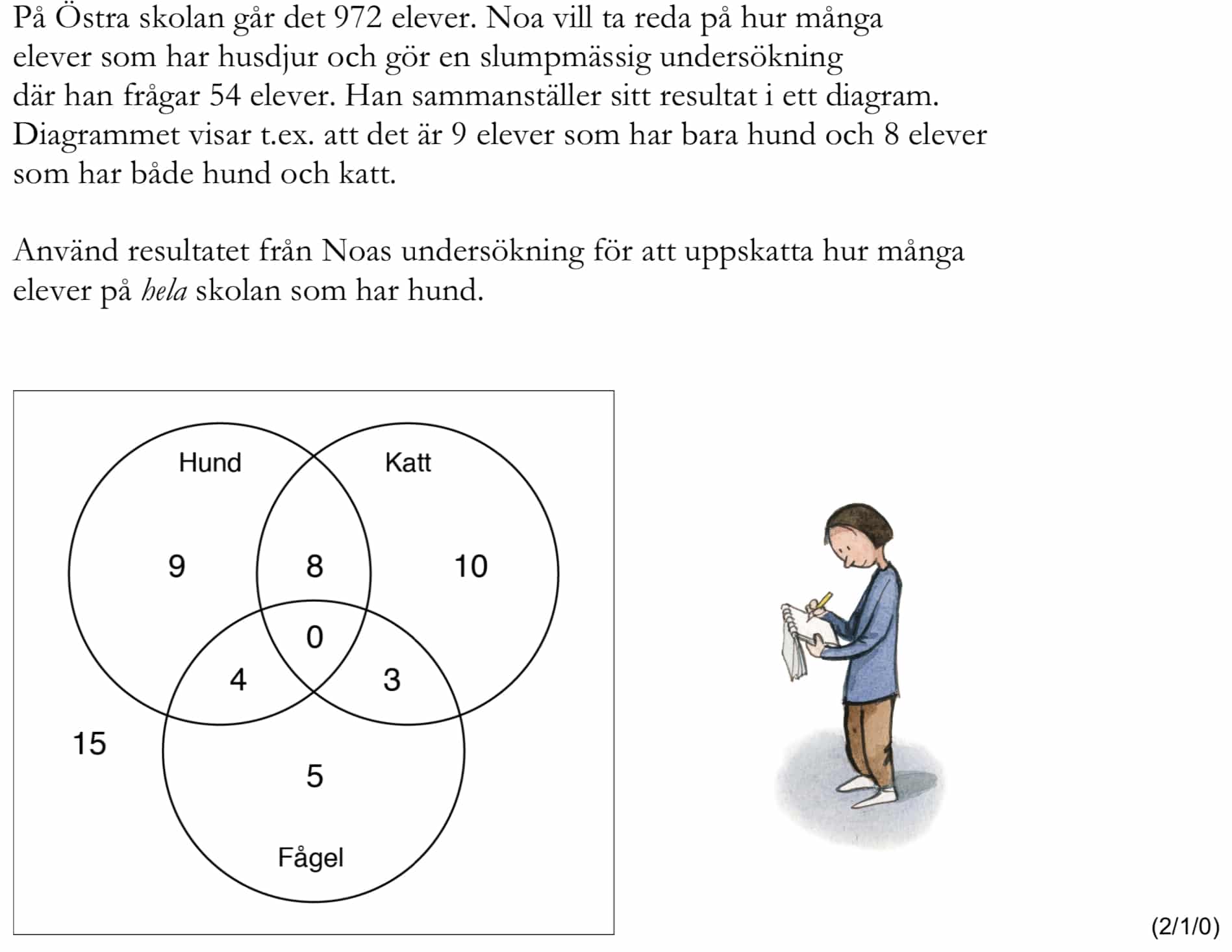
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).

Bedömningsanvisningar/facit (uppgift 3).

Från vt 2015 (Matematik årskurs 9).

Bedömningsanvisningar/facit (uppgift 20).

Från vt 2014 (Matematik årskurs 9).

Bedömningsanvisningar/facit (uppgift 21).

Från vt 2013 (Matematik årskurs 9).

Bedömningsanvisningar/facit (uppgift 25).

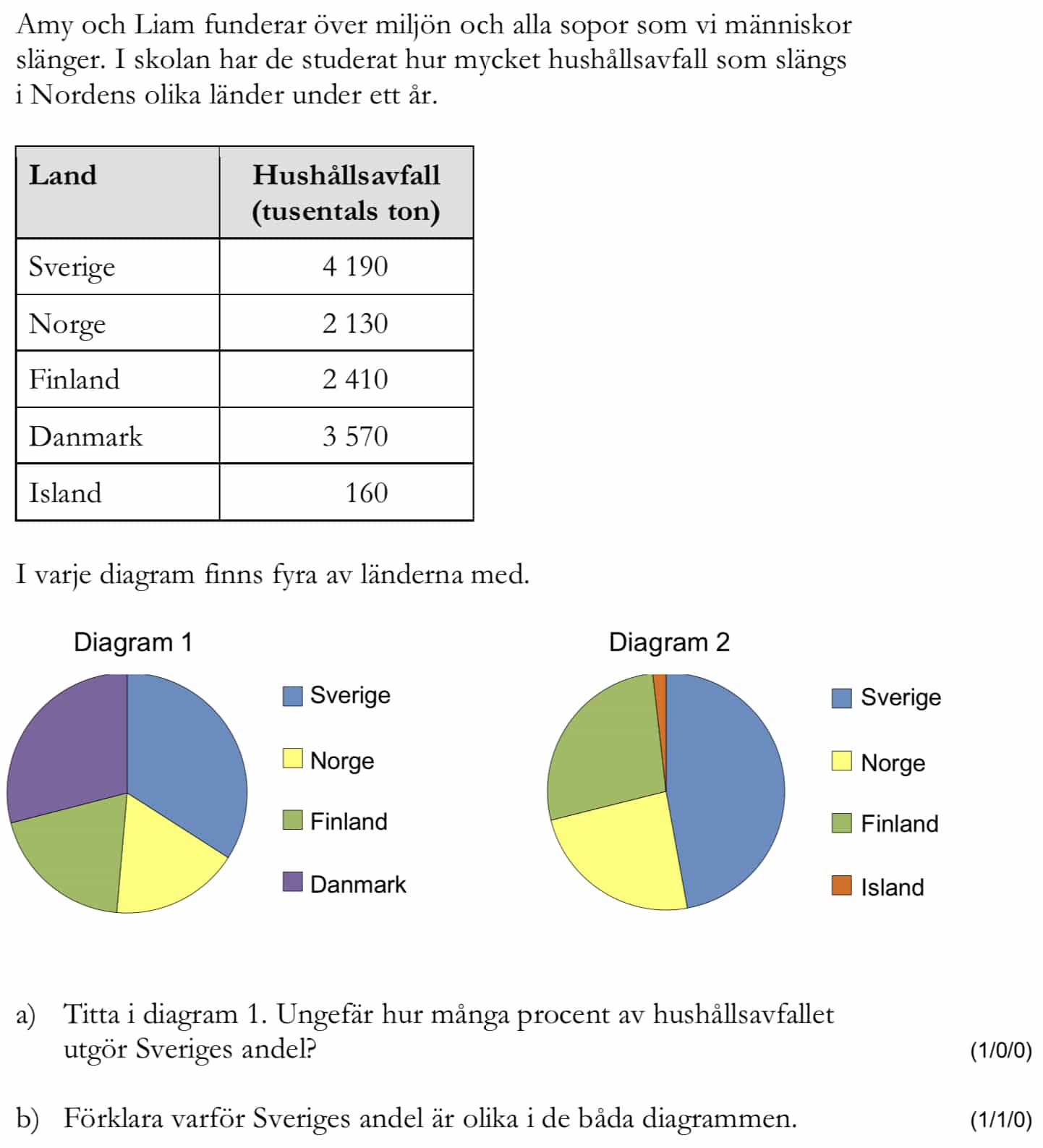
Miniräknare ej tillåten. Från vt 2015 (Matematik årskurs 9).

Bedömningsanvisningar/facit (uppgift 13).

Från HT 2012 och HT 2016 (Matematik 1a, 1b eller 1c).

Bedömningsanvisningar/facit (uppgift 21).

Från vt 2015 (Matematik årskurs 9).

Bedömningsanvisningar/facit (uppgift 25).

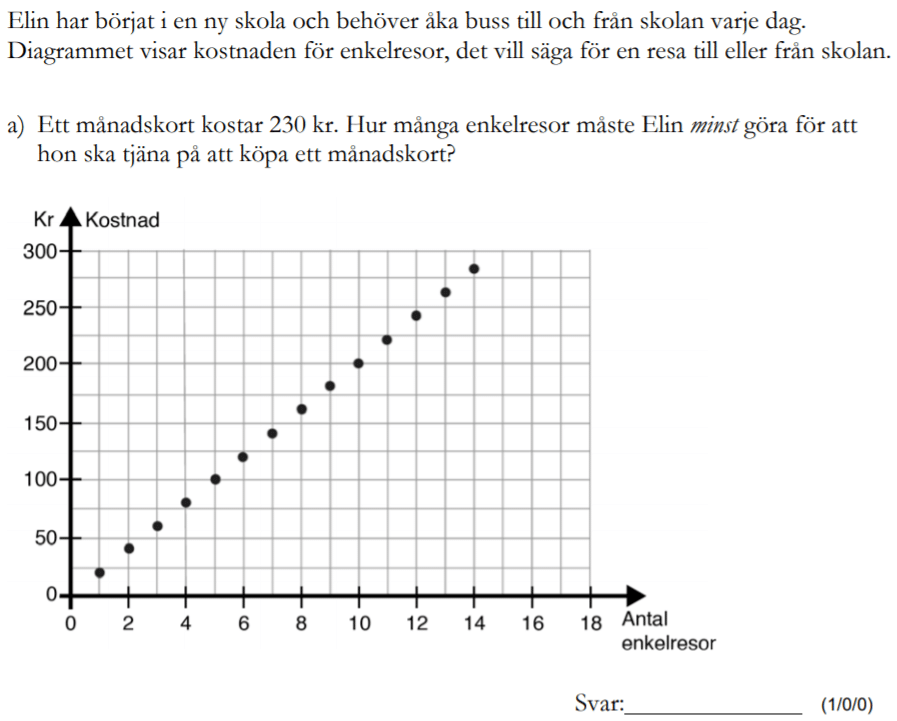
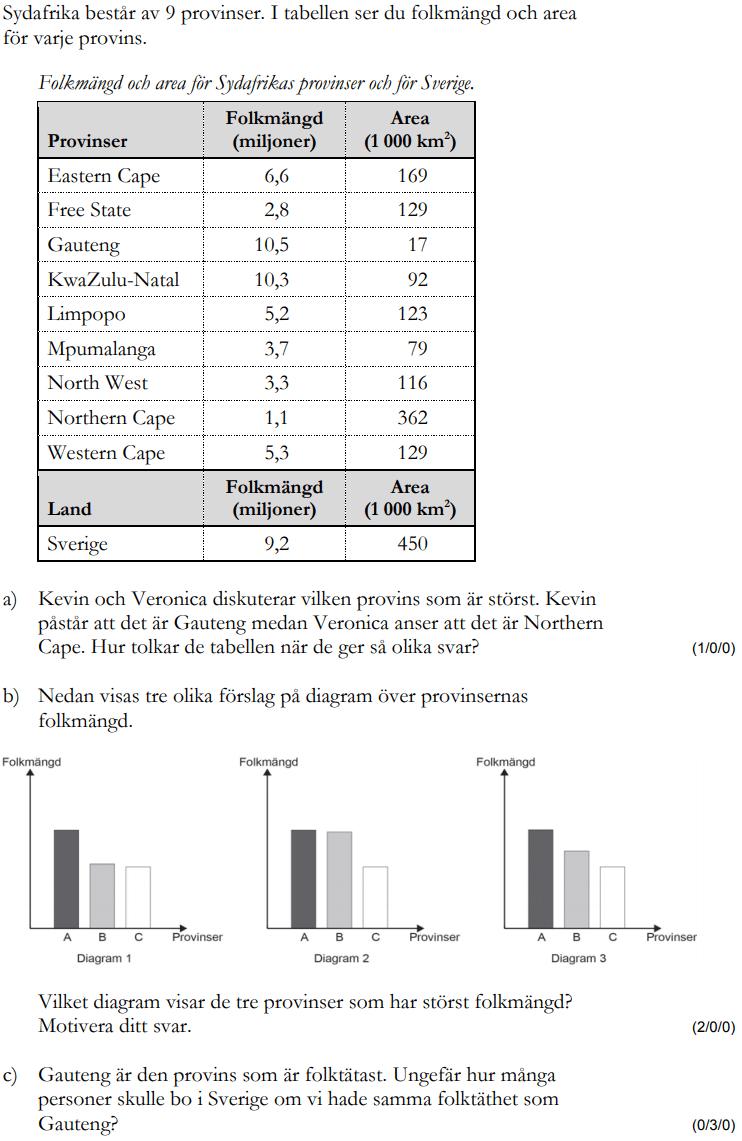
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a, 1b,eller 1c).

Bedömningsanvisningar/facit (uppgift 6).

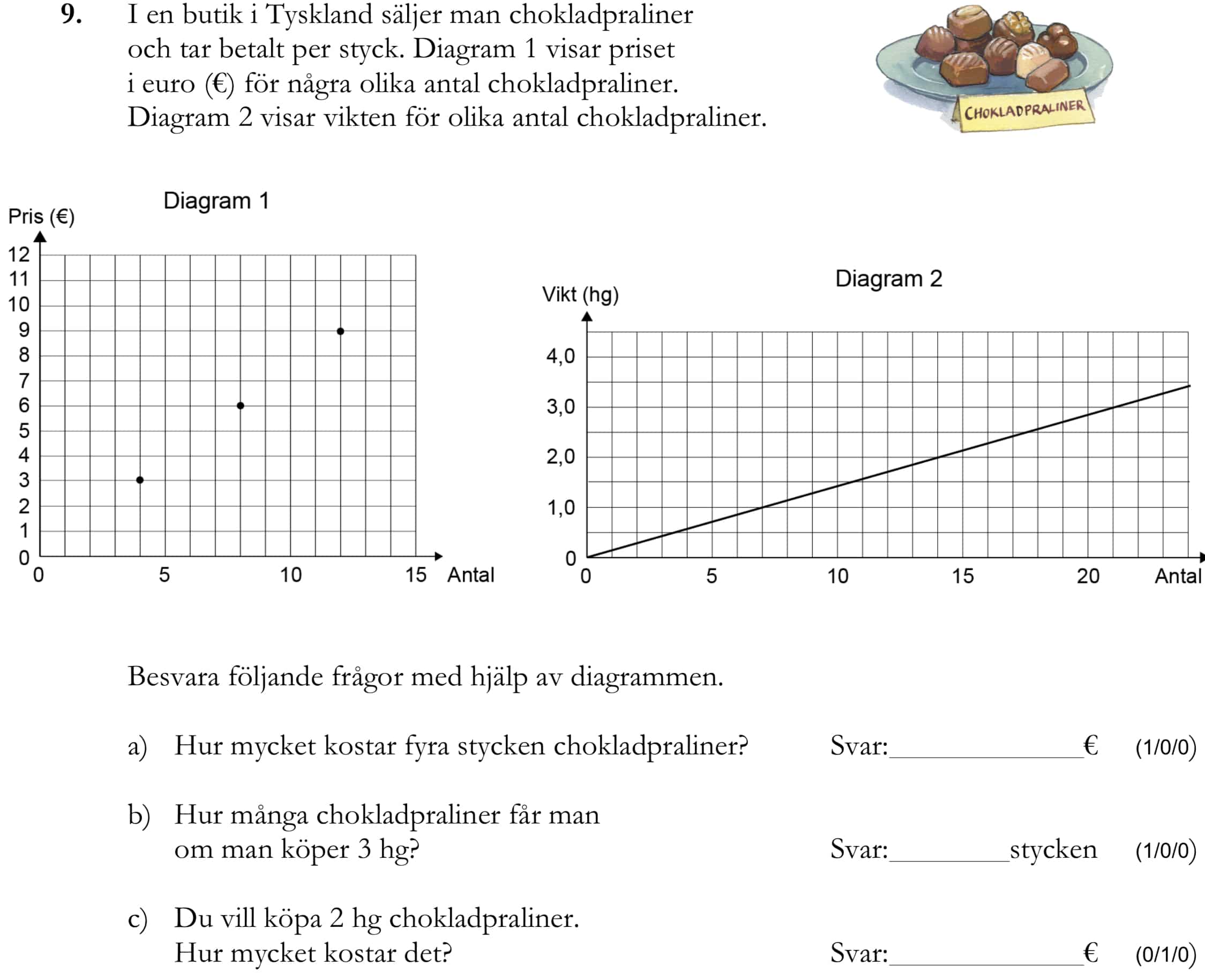
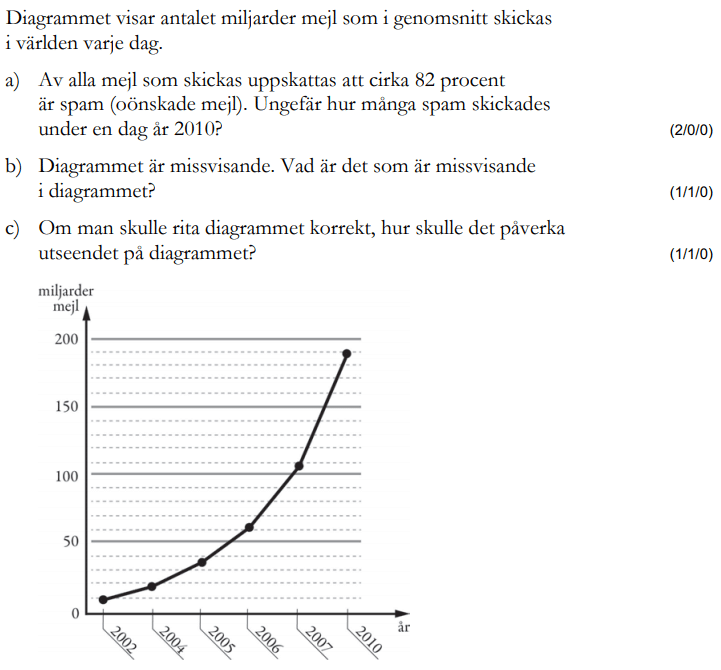
Miniräknare ej tillåten. Från vt 2014 (Matematik årskurs 9).

Bedömningsanvisningar/facit (uppgift 9).

Antal lösningar till ett ekvationssystem 2

Antal lösningar till linjära ekvationssystem

Ett linjärt ekvationssystem kan ha 0, 1 eller oändligt många lösningar

Lösningar finns alltid i de punkter där linjerna korsar varandra.

En lösning

Krav:

Linjerna har olika k-värde
(m-värdet spelar ingen roll)

Detta gör att de två linjerna lutar olika och därför kommer att korsas vid exakt ett ställe.

Inga lösningar

Krav:

Linjerna har samma k-värde.
Linjerna har olika m-värde.

Detta gör att linjerna är parallella med varandra och därmed aldrig kommer att korsas.

Oändligt många lösningar

Krav:

Linjerna har samma k-värde.
Linjerna har samma m-värde.

Detta gör att de två linjerna ligger på exakt samma position och att alla punkter på hela linjen motsvarar varsin lösning till ekvationssystemet.

Tydlig genomgång

Liknande genomgång

I inledningen visar jag också algebraiskt hur man kan se att ekvationssystemet saknar lösning eller har oändligt många lösningar.

En till ganska svår uppgift

Halvsvår uppgift med tydlig förklaring - rekommenderas!

Uppgifter från tidigare nationella prov:

Klicka på en uppgift för att se en videoförklaring till denna.

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).

Svårare uppgift

Klicka på bilden för att se videoförklaring till uppgiften!

Antal lösningar till icke-linjära ekvationssystem

Observera att ekvationssystem som innehåller exempelvis en andragradsekvation kan ha upp till två lösningar och ett med tredjegradsekvation kan ha upp till tre lösningar.

Detta beror på att graferna då kan korsa varandra vid fler platser än en.

Uppgifter från tidigare nationella prov:

Klicka på en uppgift för att se en videoförklaring till denna.

Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).