Lösa andragradsekvationer, tre bra genomgångar
Del 1: Rotmetoden och Nollproduktmetoden (faktorisering, bryta ut)
Del 2: Lösningsformeln ("pq-formeln")
Del 3: Svårare uppgifter med båda lösningsformlerna
Längre genomgång som täcker det mesta
Tittar du på denna så har du nog bra koll sen!
Hur löser man andragradsekvationer?
1. Du måste först välja rätt metod.
2. Sedan kan du börja lösa ekvationen med den metoden.
Metod 1: Rotmetoden (Kvadratrotsmetoden)
Metod 2: Nollproduktmetoden (faktorisering)
Metod 3: pq-formeln (lösningsformeln)
På formelbladet finns två formler... Du behöver inte båda!
På formelbladet finns två formler för att lösa andragradsekvationer:
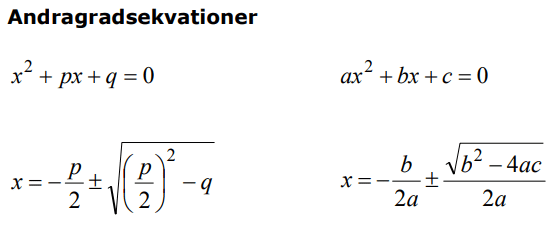
”pq-formeln” till vänster är den vanligaste att använda här i Sverige och också den formel som jag använder i genomgångarna på denna sida.
”abc-formeln” till höger är vanlig i andra länder och är framförallt smidig om du har en koefficient framför x2 -termen. ”abc-formeln” behöver du inte behärska om du kan ”pq-formeln”.
Genomgång om abc-formeln
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till denna.
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).

Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
OBS: Ett litet räknefel har smugit sig in i min videolösning här i själva svarsrutan. Fram dit är allt riktigt.

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b).

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2c).
OBS: Ett litet räknefel har smugit sig in i min videolösning på b-uppgiften precis på slutet när jag testar om den sista lösningen fungerar. Jag har av misstag skrivit -1 under rottecknet när det ska stå 1. Se bild nedan.
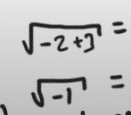
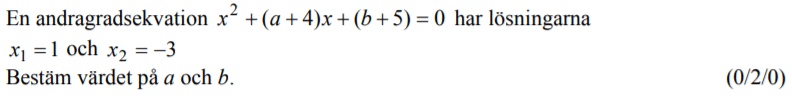
Från VT 2015 (Matematik 2c).
Nedan kommer ingenting nytt, utan bara fler genomgångar och liknande typer av material

Vill du ha fler exempel?
Fem tydliga klipp med flera exempel om hur du löser andragradsekvationer, från enkla till fullständiga. Separata klipp för varje metod.
De här klippen är bra om du vill lära dig en metod i taget, ordentligt.

Del 1: Rotmetoden (kvadratrotsmetoden)
Del 2: Nollproduktmetoden (faktorisering)
Del 3: pq-formeln (lösningsformeln)
Del 4: Något svårare uppgifter med pq-formeln.
Del 5: Vilken metod ska jag välja? (VIKTIGT!)
Lär dig de tre metoderna i en och samma genomgång:
- Rotmetoden (kvadratrotsmetoden).
- Nollproduktmetoden (faktorisering).
- pq-formeln (lösningsformeln)
Prova om du kan lösa dessa ekvationer själv:
3x2 + 1 = 13
x2 – 4x = x
x2 – 2x – 4 = 0
Kolla sedan på videolösningarna!
Lösningarna till de tre ekvationerna:
Genomgångar från klassrummet
Dessa genomgångar täcker samma innehåll som genomgångarna ovan.

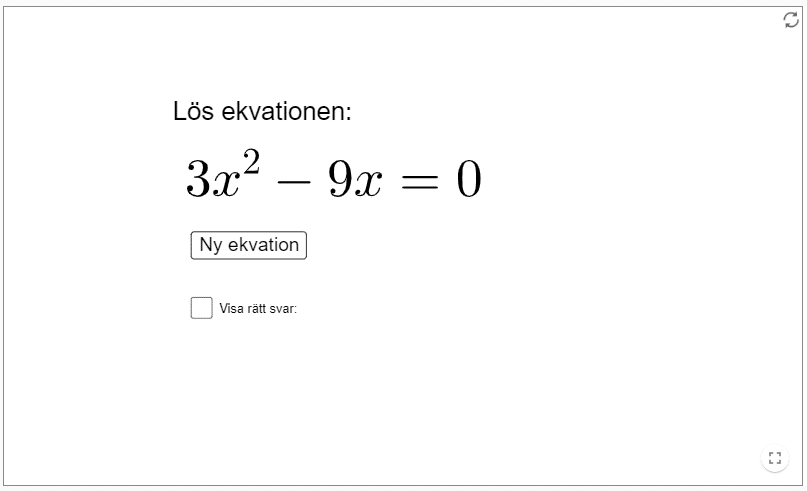

Hej den första uppgiften du räknar x2-6x+5=0 har du räknat ena x:et fel. Det ska vara x=1, inte x=2.
Hälsningar Ali
Ja precis, det ska stå x=1 och x=3. Tack 🙂
(Flyttar ner uppgiften ett par steg så den inte ligger först, och kommenterar felet där).
Hej, tack för den fantastiska hemsidan.
Vill bara säga att den första frågan på nationella prov i samma sida är felräknat. x=3-2=1. Det du har skrivit i svar är 2.
Det skriver jag endast för att hjälpa sidan att bli ännu bättre 🙂
Tack på förhand / Ali.Q
Tack Ali för att du påpekar felet och för din feedback! Det ska mycket riktigt stå x=3 och x=1 som svar på den frågan!
Kul också att du gillar hemsidan 🙂
(Flyttar ner uppgiften ett par steg så den inte ligger först, och kommenterar felet där).
Uppgift 10 b matte 2c ska stämma. Roten ur 1=-+1
VL=HL
-1=-1
Hej Ali! Ja och nej. Jag har gjort ett fel där, eftersom jag fått det till -1 under rottecknet på slutet, där ska det mycket riktigt stå roten ur 1 som du skriver (tack för att du såg det!). Däremot blir det fortfarande en falsk rot, eftersom roten ur 1 bara är 1 och inte -1.
VL=rotenur(1)=1 HL=-1.
Kvadratroten genererar enbart det positiva talet, inte det negativa. Det är därför vi skriver +- innan rottecknet när vi exempelvis löser ekvationen x^2=5, x=+-rotenur(5). Men om det bara står roten ur så är det enbart det positiva talet som efterfrågas.
Mvh Jonas
Jag vill bara säga tack för att jag skulle inte klarat matematiken utan din websida! Video förklaringarna gör en stor skillnad för mig.
Ett två år sent svar kommer här: Tack så väldigt mycket för fina kommentaren! Hoppas plugget och allt annat gått bra sedan dess! 🙂
Hej
På en av dina genomgångar angående hur man ska gå tillväga gällande pq-formeln så väljer du att lösa ekvationen genom att lämna -P/2 och P/2 upphöjt till två i bråkform istället för i decimalform, argumentet till detta är att du talar för att om man saknar digitala hjälpmedel så ska detta underlätta för en att lösa ekvationen.
På dina genomgångar av gamla prov så tillämpar du inte alls denna metod när du jobbar med pq- formeln, då väljer du att beräkna ut -P/2 och P/2 upphöjt till två och har ett annat tillvägagångssätt som, visst inte kanske skiljer sig så mycket åt, men jag hade gärna sett att du hade fått med dig det exemplet i den första videogenomgågen. När jag fick se hur du jobbade med PQ-formeln på gamla prov vart jag bara förvirrad, överlag så är du dunder vilket du säkert redan vet. Hoppas du inte uppfattar mig fel, mitt ändamål med denna feedback är bara gott.
Hej Mikael! Jag gör nog lite olika om (p/2)/2 inte blir ett heltal..
Jag tänker mig så här gällande (p/2)^2:
– Om det blir ett heltal bör du alltid räkna ut det direkt.
– Om du har tillgång till räknare är det också enklast att direkt räkna ut det i decimalform, oavsett om det är heltal eller inte.
– Om du INTE har tillgång till räknare och det inte blir ett heltal så kan du antingen arbeta med bråk under rottecknet som du skriver och så småningom ta roten ur täljaren för sig och nämnaren för sig. Här finns dock alternativ över ibland att lära sig några enkla rötter utantill som förekommer väldigt ofta, roten ur 0,25; 2,25; 6,25 och 12,25. Då kan man slippa arbeta med bråkformen även utan räknare.
Länka gärna till de direkta exemplen du hittade och skriv dit vid vilken tidpunkt jag gör uträkningarna så ser jag mer tydligt vad du menar.
🙂
Mvh Jonas
Hej Jonas och tack för denna termin. Jag har läst Ma2b på distans och dina genomgångar har varit ovärderliga. Du har också varit en stor hjälp till att jag fick 1,20 på högskoleprovet första gången jag gjorde det.
Jätte tack och hoppas du har tid och kraft att fortsätta.😃