Inspektionsmetoden - när du ser svaret.
OBS: Denna metod är bra att känna till, men det är balansmetoden som är den "riktiga" metoden och den som du måste lära dig!
Viktigt: Lösa ekvationer steg för steg med balansmetoden
OBS: Jag använder olika skrivsätt för grundskolan respektive gymnasiet:
Båda skrivsätten fungerar bra att använda när du löser ekvationer.
Skrivsättet med "väggen"
Detta använder jag i mina videor för gymnasiet. Det blir lite mindre att skriva och också lite enklare att gå tillbaka och ändra om man upptäcker att man har gjort fel. (Inte lika ”kladdigt” i uträkningen).
Enkla och mellansvåra ekvationer
Här kan du träna digitalt:
Träna steg för steg:
(Med inspiration från Alva Grönqvist)
Lös på papper, välj rätt alternativ och samla poäng:
Tips: Jättebra digital övning!
Läraren Alva Grönqvist har programmerat ihop en jättebra digital övning om att lösa ekvationer. Prova den gärna på hennes hemsida! Den är perfekt för mängdträning, vilket kan göra dig mycket säkrare!
- Länk direkt till övningen!
- Länk till hennes hemsida med massor med andra bra övningar.
Det vanligaste skrivsättet
Detta använder jag i mina videor för grundskolan. De flesta gymnasielärare använder också detta skrivsätt.
Enklare ekvationer
Svårare ekvationer
Fler liknande genomgångar om balansmetoden
Nivå 1: Enkla ekvationer
Nivå 1, forts: Negativt antal x
Nivå 2: x i båda led (på båda sidor)
Nivå 3: Förenklingar krävs
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a).
Bedömningsanvisningar/facit (uppgift 8).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 2).
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1c).
Bedömningsanvisningar/facit (uppgift 1).
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 10).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 6).
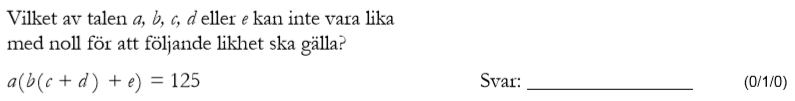
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 11).
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1c).
Bedömningsanvisningar/facit (uppgift 9).
Fantastisk! Pedagogiskt och lättförståeligt, tack!
Hej Anna! Stort tack för de fina orden! ☺️😊 Lycka till med matten! Mvh Jonas
Detta har varit till en otrolig hjälp, tack så jättemycket!
Tack så mycket jag hade väldigt svårt att förstå men efter de här video har jag blivit bättre på det!!!!
Periodddd
tbh du måste få betalt från kommunen för ditt jobb. Du lär ut mer matte än vad hela göteborgs kommun gör, tack aå mycket för dina genomgångar.