Tydlig genomgång över det mesta som är viktigt (tre exempeluppgifter)
...om hur vi hittar extrempunkter och terrasspunkter samt bestämmer karaktären med hjälp av andraderivata eller teckentabell.
En liknande exempeluppgift från ett nationellt prov, men något enklare:
Gör gärna denna uppgift som träning direkt efter att du har sett genomgångarna ovan.

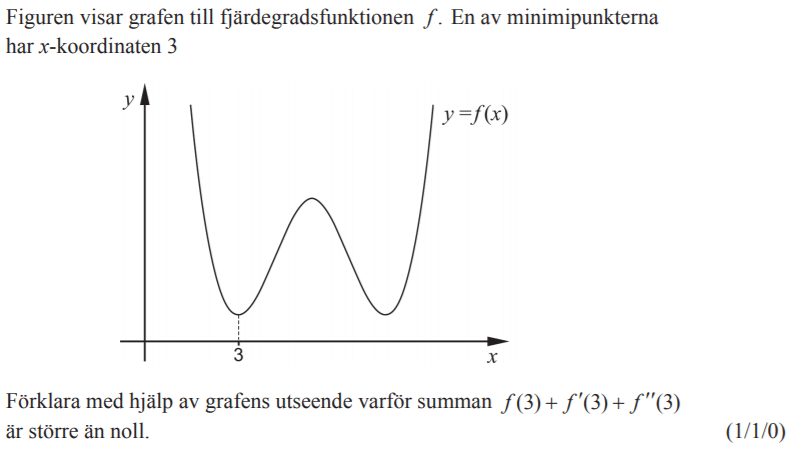
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 3b och 3c)
Bedömningsanvisningar/facit (uppgift 13).
En liknande exempeluppgift.
OBS, korrigeringar gällande genomgångarna nedan:
I flera av klippen nedan gör jag två återkommande fel:
- En terrasspunkt är inte en extrempunkt, trots att jag i flera videor säger det. Till begreppet extrempunkt hör maximipunkt och minimipunkt.
Ändpunkterna i intervallet (definitionsmängden) räknas också som maximipunkt eller minimipunkt (och därmed extrempunkt) om kurvan antingen går uppåt eller nedåt där. - Om andraderivatan är 0 i en punkt som också har lutningen 0 kan vi inte dra slutsatsen att punkten säkert är en terrasspunkt. Om andraderivatan är 0 så måste vi visa karaktären med hjälp av teckentabell istället.
Oftast gäller att om andraderivatan är 0 så är det en terrasspunkt, men det finns undantag. Ett undantag är f(x) = x4 som har en minimipunkt, men där andraderivatan i den punkten ändå är 0.
Längre sammanfattande genomgång
...om hur vi hittar extrempunkter och terrasspunkter samt bestämmer karaktären med hjälp av andraderivata eller teckentabell.
Du bör titta på denna genomgång som repetition, inte som första genomgång över området tror jag…
Rekommendation: Fyra uppdelade klipp över de viktigaste delarna i det här området:
Del 1: Beräkna startvärde (repetition!)
Del 2: Beräkna nollställen (repetition!)
Del 3: Hitta extrempunkterna (viktigt!)
OBS: Det är bara minimipunkter och maximipunkter som räknas som extrempunkter. Terasspunkt är ett eget begrepp. Principen är dock lika för hur man räknar ut en sådan.
(Insikt nyligen).
Del 4: Skissa grafen med hjälp av teckentabell (viktigt!)
Extremvärden och derivatan
Att rita grafen med hjälp av teckentabell
Att hitta och undersöka extremvärden till en funktion genom att använda derivata och teckentabell.
En till liknande genomgång som tar upp följande:
- Beräkna startvärde
- Beräkna nollställen
- Beräkna var extrempunkterna finns (x-värde och y-värde)
- Rita teckentabell
- Rita graf
Andraderivatan och extrempunkters karaktär
Vad är andraderivata och hur kan vi använda den för att bestämma en extrempunkts karaktär?
… det vill säga om det är en minimipunkt, maximipunkt eller terasspunkt.
Rekommenderas!
Mot högsta betyg:
Att undersöka grafens utseende för potensfunktioner, där x är i nämnaren.
Denna genomgång är bra för dig som siktar mot de högsta betygen!
Stort sammanfattande klipp på allt det viktiga
Att undersöka en graf: ta reda på ALLT" och sedan skissa grafen.
- Startvärde
- Nollställen
- Extrempunkters läge
- Extrempunkters värde (extremvärden)
- Extrempunkters karaktär (min, max eller terass?)
- Intervall där funktionen är strängt växande eller strängt avtagande
- Definierad för alla x?
Tre exempel från E-nivå till C-nivå.
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till den!

Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 3b och 3c)
Bedömningsanvisningar/facit (uppgift 13).

Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 12).
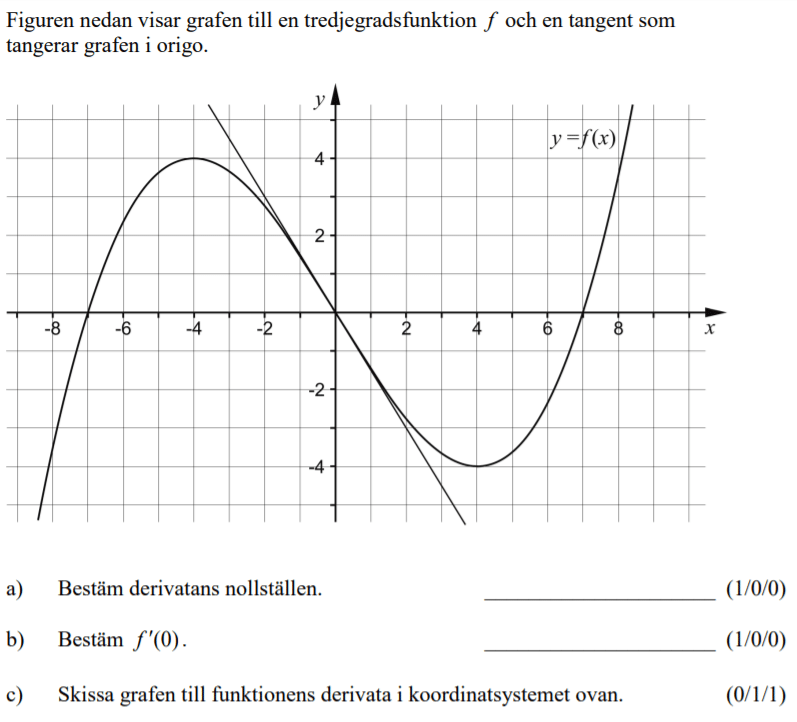
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 6).
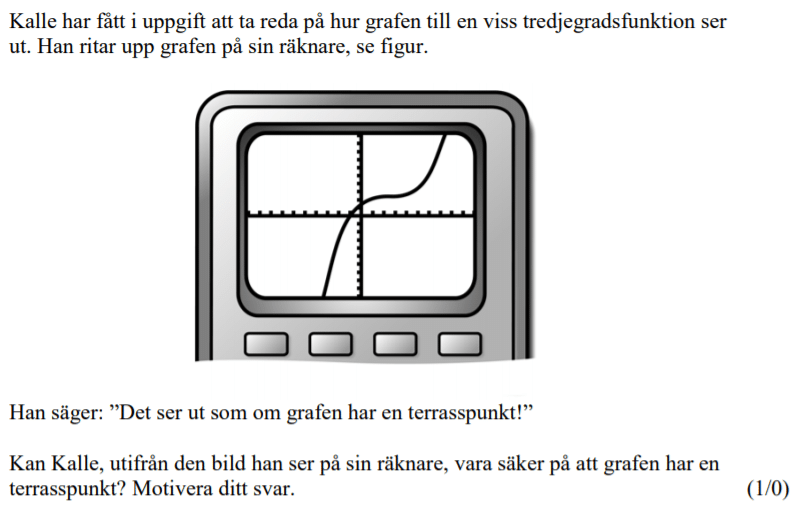
Löses utan digitala hjälpmedel.
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 3).
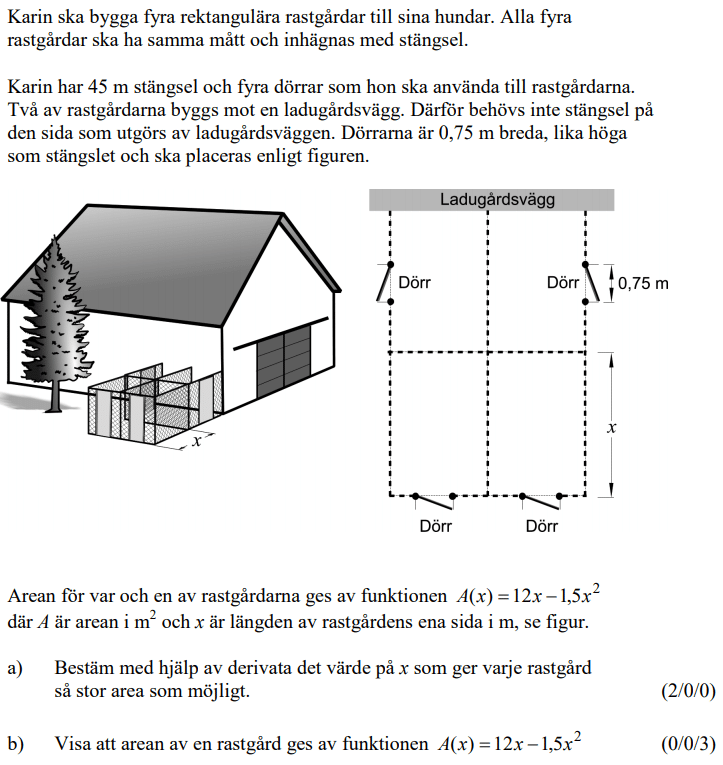
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b och 3c)
Bedömningsanvisningar/facit (uppgift 12).
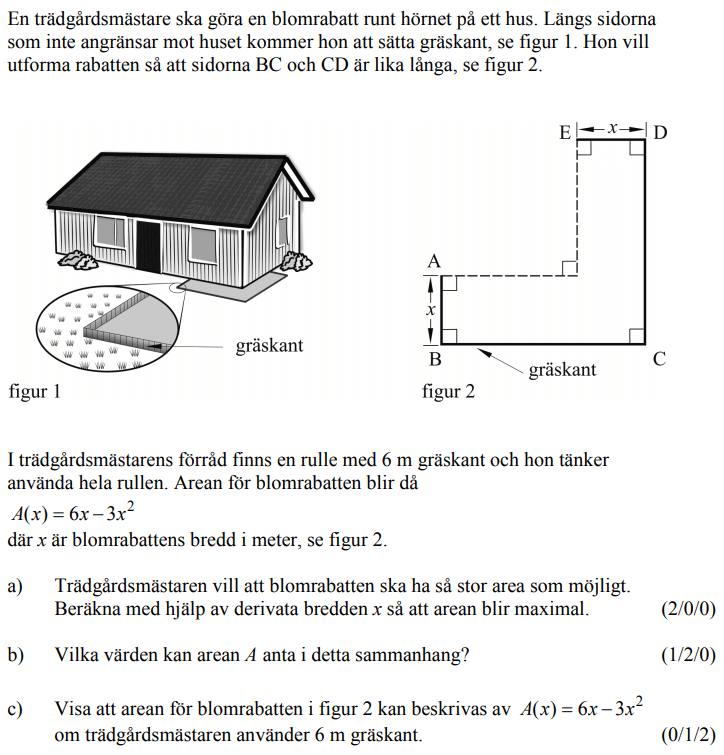
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 13).
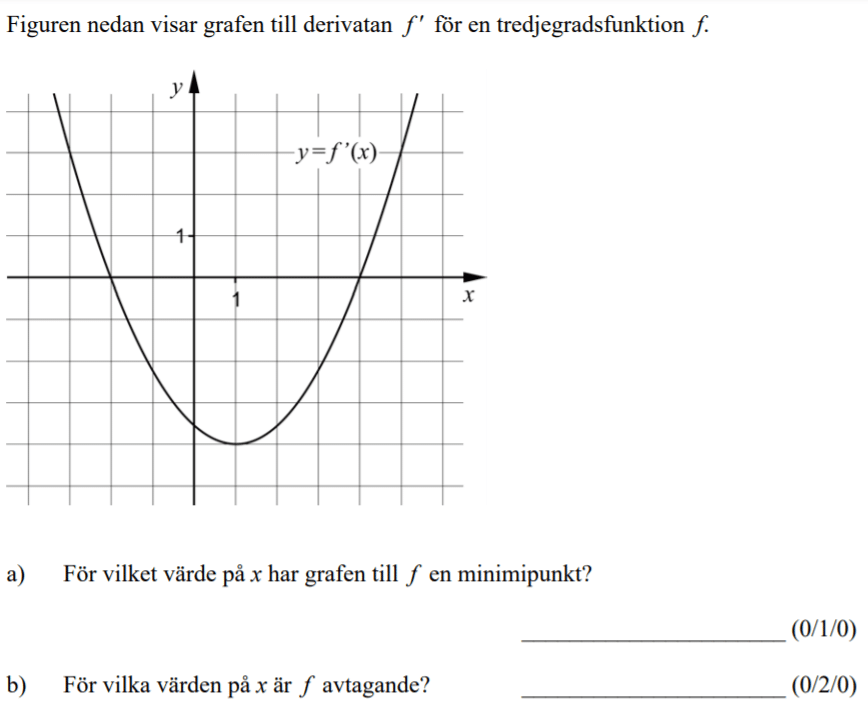
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 7).
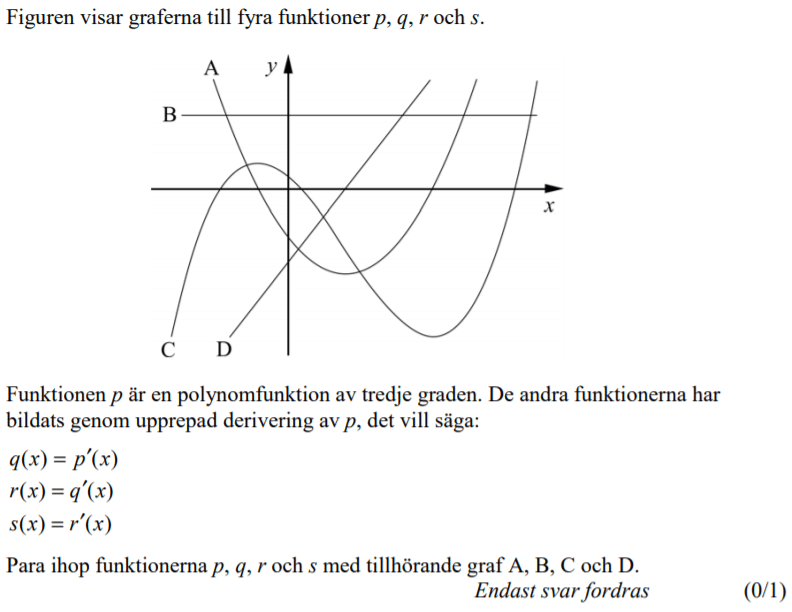
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 12).
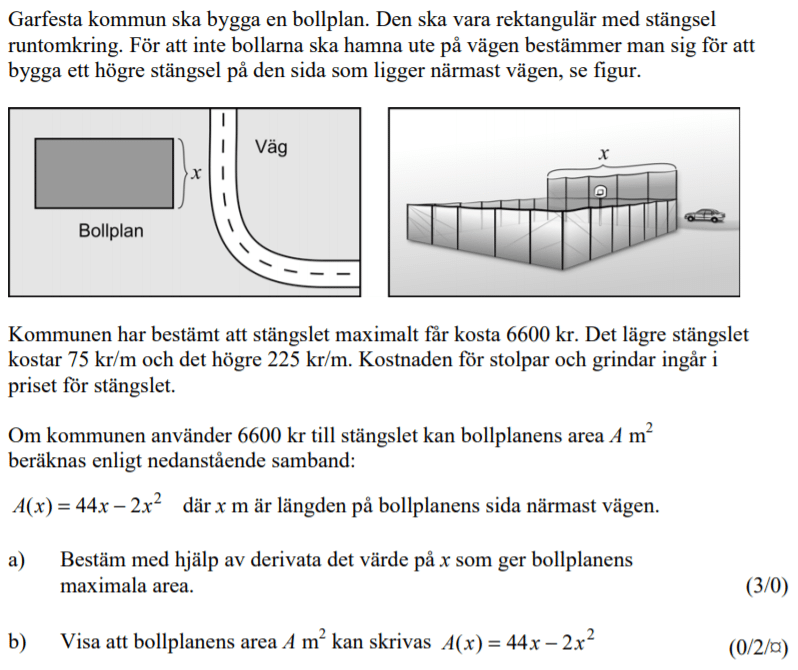
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 13).

Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 23).


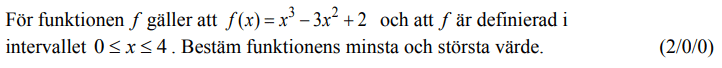


du är en ängel, kan inte vara mer tacksam
Hej Maryam! Ååh tack för de orden! Önskar dig stort lycka till med matten, GO STRONG! 🙂 Mvh Jonas