Större sammanfattande genomgångar
Grafen till en polynomfunktion, samt hur man skriver funktionen om man ser grafen
Grafen till en polynomfunktion
- Hur många gånger vänder grafen?
- Hur många nollställen kan funktionen ha?
- Åt vilket håll "avslutar" grafen?
- Vad är en dubbelrot eller trippelrot?
Antal reella nollställen:
– Förstagradsfunktion (linjär funktion): 0 eller 1 nollställe.
– Andragradsfunktion: 0, 1 eller 2 nollställen.
– Tredjegradsfunktion: 1, 2 eller 3 nollställen.
– Fjärdegradsfunktion: 0, 1, 2, 3 eller 4 nollställen.
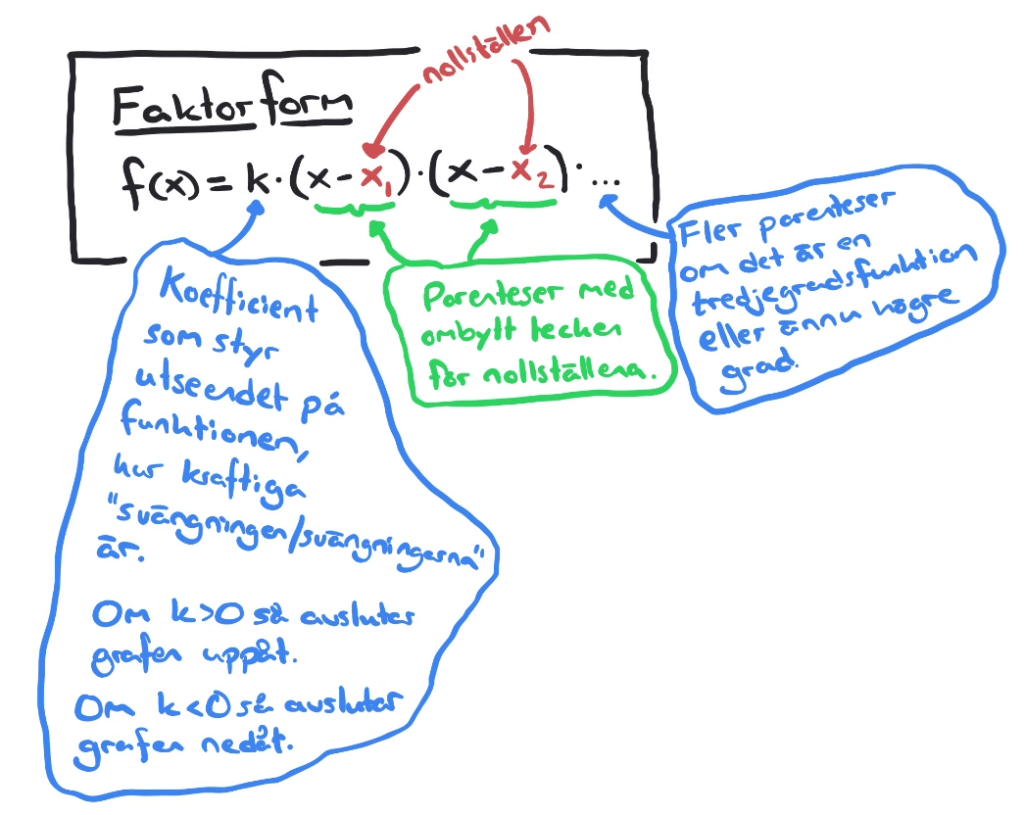
Faktorform och nollställen
Att skriva funktionen till en graf, med hjälp av faktorform
Om du ser grafen till en polynomfunktion och får i uppgift att bestämma funktionen så kan du använda dig av faktorform.
Liknande genomgång med andra exempel
Enklare genomgång som tar upp mer allmänt om utvecklad form och faktorform
Nollställena syns direkt om polynomet/funktionen är faktoriserat!
Tydlig sammanfattning: FAKTORFORM, NOLLSTÄLLEN, SKRIVA FUNKTIONEN TILL EN GRAF samt DUBBELROT
GeoGebra-övning:
Undersök och förstå grafen till:
- Tredjegradsfunktioner
- Fjärdegradsfunktioner
Rekommenderas starkt


”Not all heroes wear capes”