Integraler
Liknande genomgångar, kanske med enklare exempel:
Integraler, del 1: Vad är en integral och hur uppskattar man värdet av en integral?
Integraler, del 2: Hur beräknar man en integral?
Integraler: så här skriver man!
Liknande genomgång
Liknande genomgångar över vad integraler är och hur man beräknar sådana.
Beräkna en integral (arean under graf) snabbt med digitala verktyg
På den del på ett nationellt prov där du får använda digitala hjälpmedel är det fullt tillåtet att använda funktionerna nedan. Du måste dock på pappret beskriva vilket verktyg du använd, vad du skrivit in i detta och vad du fått för resultat.
GeoGebra:
Testa genom att ändra direkt bredvid.
På grafräknaren:
TI-82, TI-83, TI-84, m.fl.
Kommandot fnInt( hittar du om du trycker på knappen MATH och bläddrar nedåt.
Du skriver fnInt( funktionen , x , från , till ) med kommatecken mellan (använd ej punk). Till skillnad mot på GeoGebra behöver du skriva dit att du använder variabeln x.
På TI-84 ser detta annorlunda ut och mer likt hur vi skriver på papper.
Bevis:
Hur kan den primitiva funktionen ge arean under en graf?
Det ingår inte i Matematik 3 att förstå detta bevis. Däremot är det en vanlig fråga hur det kommer sig att en primitiv funktion motsvarar en area.
Översumma och undersumma
Översumma, undersumma, integral och hur vi ställer upp och beräknar en integral
Geogebradokumentet som används i klippet återfinns i gröna rutan längre ned på sidan.
Att undersöka arean under en graf med översumma och undersumma
Klicka på bilden och prova dig fram!
Trick i GeoGebra för integraler: Att ta reda på okänd integrationsgräns med nlös().
Integraler: Uppgifter
En exempeluppgift
Uppgifter från boken
Origo 3b.
Uppgifter: 5202, 5204, 5211ab, 5212, 5213, 5214a, 5215.
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till den!
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
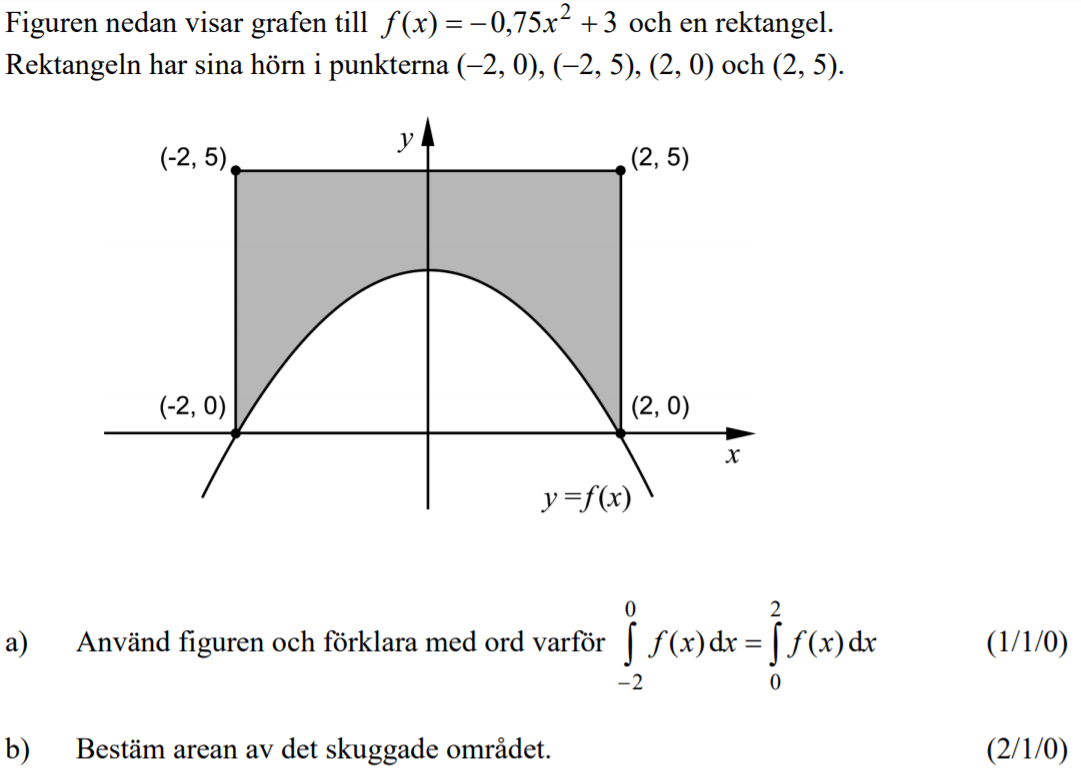
Från HT 2013 (Matematik 3b och 3c)
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b och 3c)
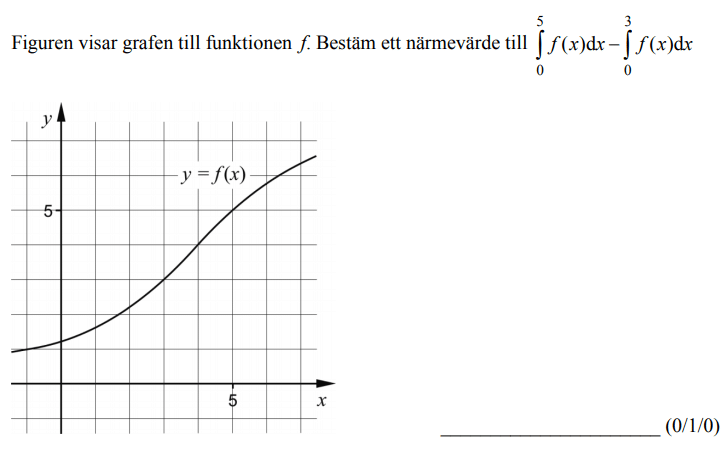
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
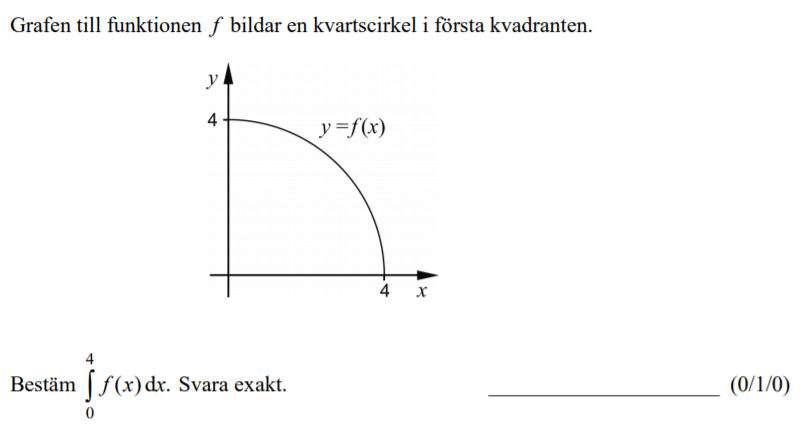
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b och 3c)
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 3b och 3c)
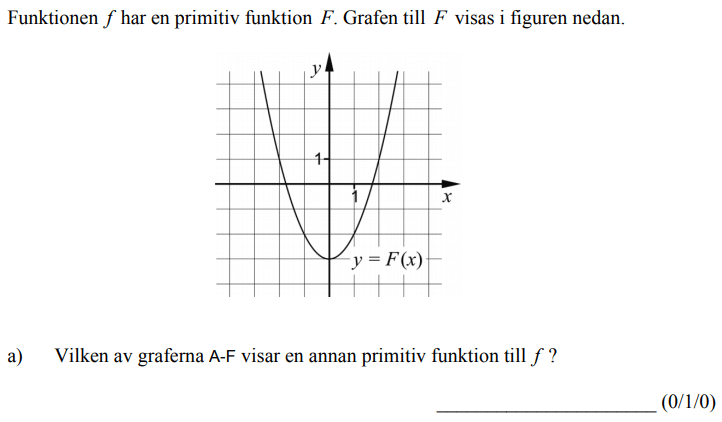
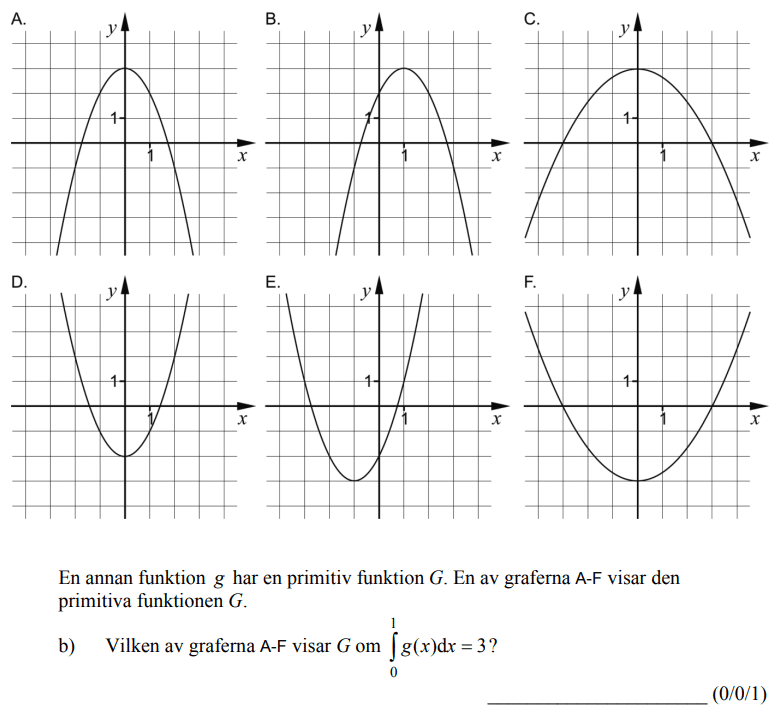
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
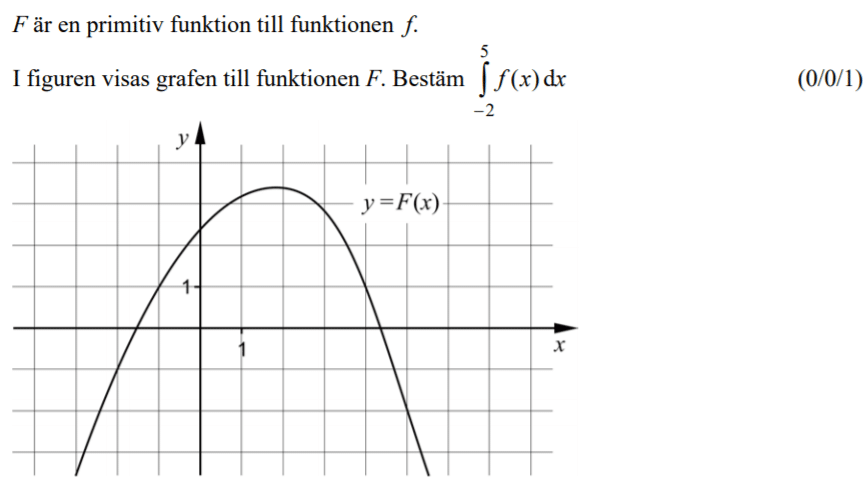
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
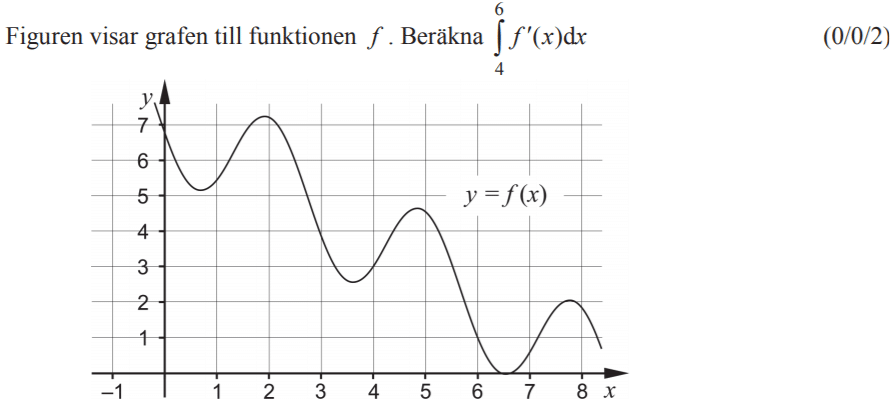
Från VT 2014 (Matematik 3b och 3c)
Asså tack som fan för att denna sidan finns 😌🙌😭
Schysst kommentar! 😀 Tack för det! Kul att du gillar sidan!
Lycka till med matten 🙂
Mvh Jonas
Det här sidan hjälper hemskt mkt med matten. Tack så mkt. Men önskar liksom att du hade lite mer A uppgifter, alltså utöver de NP uppgifter som redan finns.
Hej! Vad härligt att höra! Ta en titt här, jag har nu spelat in en sändning med ett gäng riktigt svåra uppgifter till. https://youtu.be/QV0BA5GByBA
Hoppas de kommer till nytta 🙂 De finn s också upplagda under https://vidma.se/np3 nu.
Hej! Kan du inte visa hur man löser uppgift 5205 & 5206 i origo 3b. Förstår inte hur man ska göra.
Hej! Det här blir ett för sent svar, men jag har inte alls haft tid för detta tyvärr… Jag hoppas att det har gått bra för dig ändå 🙂