Repetition av grunder från tidigare kurs
Det viktigaste om integraler!
Primitiva funktioner
Primitiva funktioner och integraler
Primitiva funktioner och integraler, samt beräkna area mellan grafer
Längre genomgång: Integraler, area under grafer. Svårare exempeluppgift med trigonometri.
Svårare uppgift om area mellan grafer
Dessutom med knep om hur vi löser en trigonometrisk ekvation som dyker upp: cos x = sin 2x.
OBS: Ekvationen cos x = sin 2x kan även lösas med följande metod, vilket förmodligen är enklare än metoden i videon:
2sinxcosx = cosx | -cosx
-> 2sinxcosx – cosx = 0
-> cosx(2sinx – 1) = 0
Nollproduktmetoden ger två fall:
- Fall 1: cosx = 0 ger x = π/2 + nπ
- Fall 2: 2sinx – 1 = 0 -> sinx = 1/2 -> x = π/6 + n2π samt x = 5π/6 +n2π
Dessa svar är ekvivalenta (lika) som de jag ger i videon, men skrivna på ett annat sätt.
Trick i GeoGebra för integraler: Att ta reda på okänd integrationsgräns med nlös().
Beräkna area mellan grafer, fler genomgångar
Svårare exempel:
Enheter för integraler
Uppgifter från tidigare nationella prov, med videoförklaringar
Klicka på en uppgift för att se en videförklaring till den.
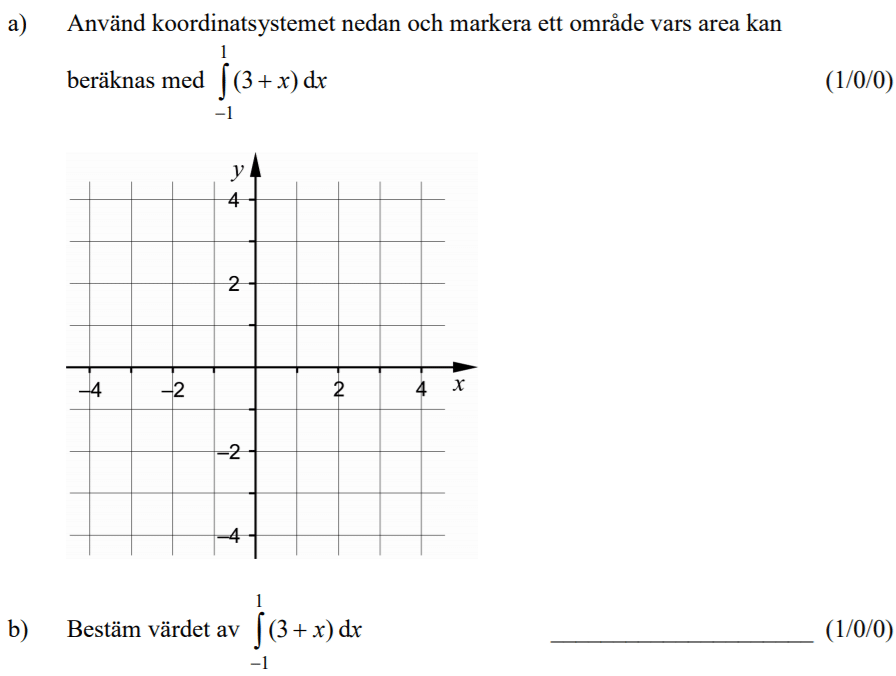
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
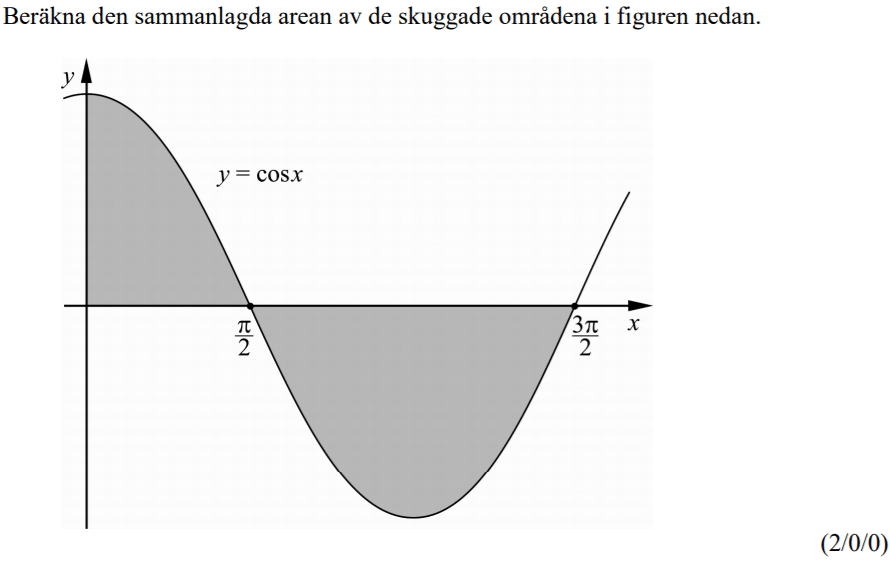
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
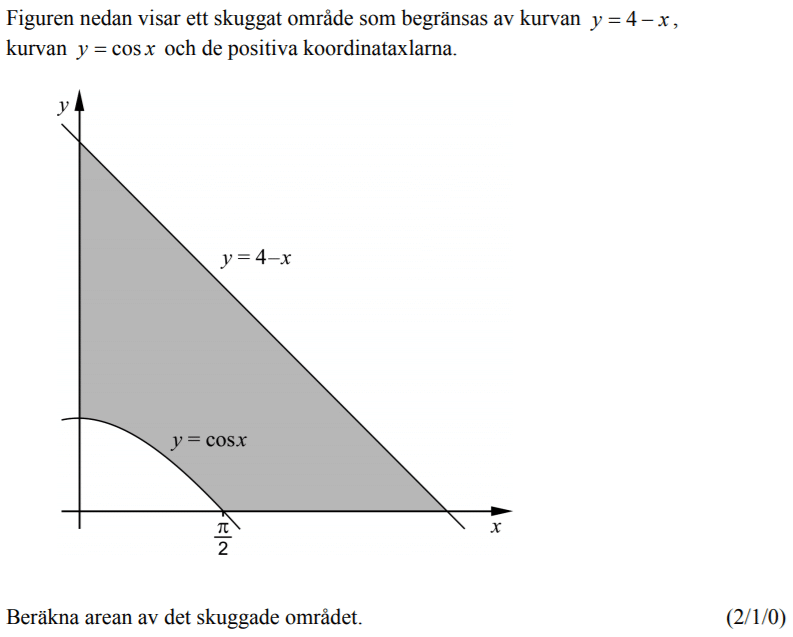
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).
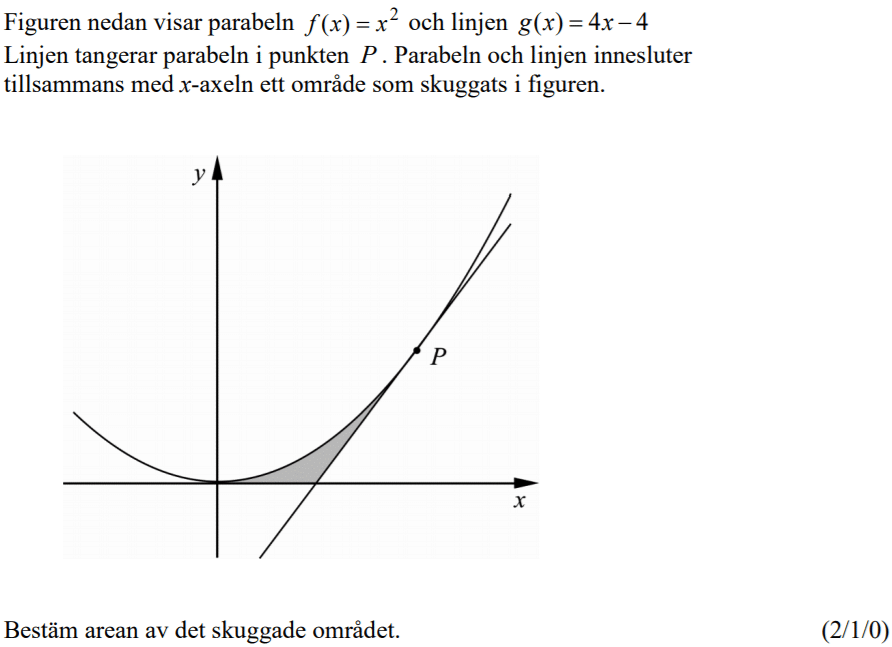
Från HT 2013 (Matematik 4).

Från VT 2014 (Matematik 4).

Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).

Från HT 2013 (Matematik 4).
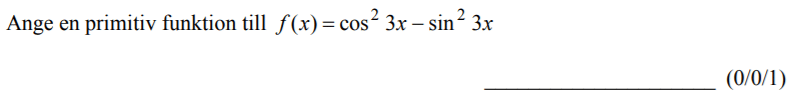
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
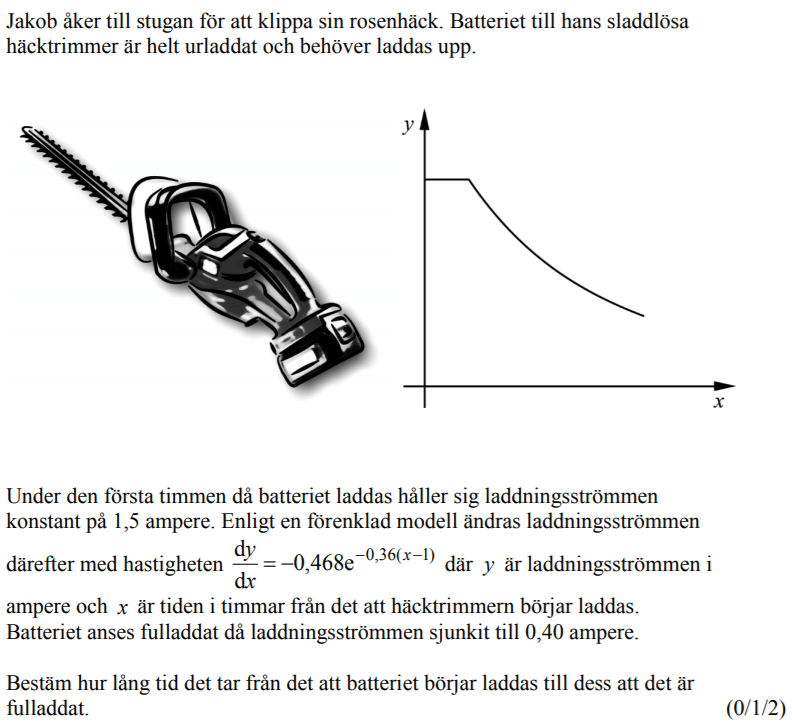
Från VT 2014 (Matematik 4).

Hej Jonas, tack för denna fantastiska hemsida, ska skriva NP nästa vecka och detta är guld värt. Att du erbjuder detta gratis är fantastiskt. Jag har också en fundering. I tredje uppgiften ovan så räknar du ut det genom att ta 2 integraler subtraherat med varandra. I genomgången ovan (den som var för matte 4 och 5) så säger du att man kan ta integralen för den övre funktionen – den undre, är det bara 2 olika sätt att lösa uppgifterna på och hade det fungerat även på den tredje uppgiften ovan? Återigen tack! Dina pedagogiska förklaringar är vad som fått mig att börja förstå den avancerade matten.
Hej! Nu kommer ett väldigt sent svar på denna kommentar, men utifall någon annan funderar på samma så…
Det går att göra på båda sätten och båda fungerar lika bra. Att ta två separata integraler kan vara lättast att förstå Varför det fungerar, men det går ofta snabbare om man skriver det som en enda. Men svaren blir lika.
Tack för fina orden om hemsidan! 🙂 🙂 Hoppas kursen gick bra!
DU är guldvärt. Jag tycker att du ska statsa på att skriva egna matte böcker. Ditt sätt att förklara skulle få dina böcker att bli väldigt populära än de tråkiga som vi har nu och som bara innehåller jobbiga, kortfattade genomgångar.
Tack för hjälpen!
Stort tack för feedbacken! Jätteglad för de orden. 🙂
Jag har tänkt tanken, men jag tror att det är svårt (svårare) att göra det tydligt i skrift. Kanske försöker jag någon gång, vem vet!
Mvh Jonas
Hej Jonas,
Liten fundering kring en lösning i en av videorna där vi ska bestämma integrationsgränsen mellan funktionerna g(x)=cosx och f(x)= sin2x.
Detta borde ge ekvationen cosx=sinx2x och med formeln för dubbla vinkeln kan det skrivas om till cosx=2sinxcosx och förenklar vi den lite borde vi hamna vid 1/2=sinx. Detta värde hittar vi på pi/6 och 5pi/6. I videon är det ett annat värde för integrationsgränserna. Har jag gjort något fel och vad kan jag ha missat? Super tacksam för svar!
Vill också bara säga ett stort tack för allt ditt hårda jobb och fantastiska videos, de är guld värda!
Mvh
Marcus
gärna mer om hur det funkar att ta fram primitiva funktioner från tex sin(kx)