Letar du efter tillämpningsuppgifter? Gå hit istället:
Kedjeregeln i ord
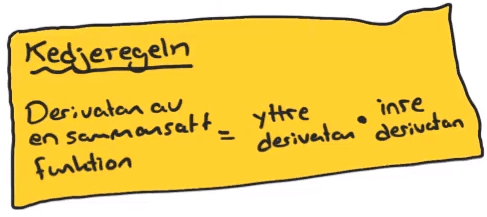
Kedjeregeln:
Derivatan av sammansatta funktioner, tex:
OBS: Filmen nedan startar mitt i genomgången, när jag börjar visa själva metoden. Spola tillbaka om du vill se en halvrörig förklaring till varför kedjeregeln funkar.
Kommentar till genomgången ovan.
När jag skriver upp den inre och yttre derivatan i exemplen skriver jag slarvig notation och skriver y’ istället för exempelvis y'(u). ´Jag anser att den delen av uträkningen är mer en stöduträkning än att den behöver skrivas helt korrekt. Här kommer en kort förklaring om hur det går att skriva om man vill vara superkorrekt:
Skriv upp svaret direkt om det är enkelt att se!
Exempeluppgifter, enkla och svåra!
Fler genomgångar nedan ...
...men i dessa genomgångar använder jag inte skrivsättet med pilarna. Jag tycker pilarna förenklar dock och kommer gå över till det skrivsättet helt.
Inledande genomgång om kedjeregeln: Att derivera sammansatta funktioner
Genomgångar med exempeluppgifter
Några blandade uppgifter med produktregeln, kvotregeln och kedjeregeln
Uppgifter: Fyra enklare samt en jättesvår A-uppgift

Kedjeregeln:
Svår A-uppgift. (Oredigerad och lite rörig uträkning).
Förklaring till varför kedjeregeln fungerar, samt nya beteckningar för derivata
Ny beteckning för derivata är dy/dx som innebär samma sak som y'(x).
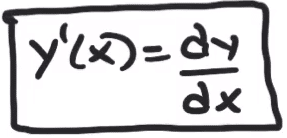
Beteckningarna f(g(x)) och f’(g(x))
Tillämpningsuppgifter
Tillämpningsuppgifter handlar nästan alltid om samband mellan olika förändringshastigheter, tex liter/dm, dm/min och liter/min i samma uppgift. Detta finns i ett eget avsnitt på Vidma: https://vidma.se/forandringshastigheter/
Uppgifter från tidigare nationella prov, med videoförklaringar
Klicka på en uppgift för att se en videförklaring till den.
Kommentar: a-uppgiften handlar om kedjeregeln.

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
Kommentar: a-uppgiften handlar om kedjeregeln.

Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).

Från HT 2013 (Matematik 4).
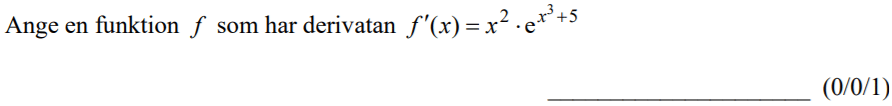
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
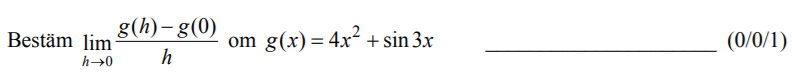
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).
