Kontinuerliga och diskuntinuerliga funktioner, samt diskreta funktioner
Kontinuerlig funktion
En funktion är kontinuerlig om dess graf är sammanhängande för alla värden som tillhör definitionsmängden. Med sammanhängande betyder att det går att rita grafen utan att lyfta pennan.
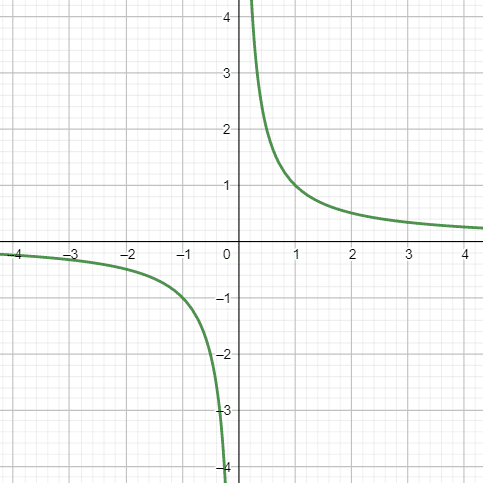
Observera att exempelvis f(x)=1/x också är kontinuerlig, trots att hela grafen inte hänger ihop. Detta beror på att x=0 inte tillhör definitionsmängden (nämnaren får aldrig vara 0) och därför spelar det ingen roll att det sker ett ”hopp” precis där. Funktionen är kontinuerlig (sammanhängande) för x < 2 och för x > 2, vilket innebär att den är det för alla x som tillhör definitionsmängden, alltså för alla x som funktionen gäller för.
Kontinuerlig, trots att det inte ser ut så:
Diskret funktion
En funktion är diskret om ingående värden på x är diskreta. Med diskreta värden menas att de är åtskilda värden, exempelvis heltal.
Diskreta funktioner är funktioner som bara gäller för exempelvis heltal.
Ett exempel kan vara en funktion för intäkter, som beror på antalet sålda produkter (vi kan ej sälja 3,18 produkter, bara heltal). Ett annat exempel är en funktion för arean av figur n, där vi har en följd av växande figurer. Funktionen är diskret eftersom figurnumret (n) naturligtvis måste vara heltal.

Sjukt bra hemsida! detta räddar mitt matte betyg nu under distansundervisningen. Denna sida bör rekommenderas för alla elever i gymnasiet för att underlätta när man inte har några fysiska lektioner.
Tack Jonas för hjälpen!
Tack så jättemycket för den kommentaren, William! ☺️😁 Det gläder mig! Stort lycka till med plugget! Mvh Jonas
Ni är så bra 🙂
Stort tack ☺️ Vad bra att du gillar det! Ha det toppen! Mvh Jonas
Helt fel f(x)=1/x är inte kontinuerlig om definitionsmängden (x tillhör de reella talen/ x inte 0).
Bara att x är skilt från 0 gör att diskontinuerlighet gäller. Men om definitionsmängden är x>0 eller x<0 så är den kontinuerlig.
Ta bort detta.
Hej Lasse!
Tack för din återkoppling.
Jag vet att det finns viss oenighet om huruvida dessa funktioner är att betrakta som kontinuerliga eller ej. Jag har också sett flera diskussioner om detta i gruppen Matematikundervisning för matematiklärare på Facebook där varje diskussion har slutat med slutsatsen att de _är_ kontinuerliga – för hela sin definitionsmängd.
Du skriver att ”Men om definitionsmängden är x>0 eller x<0 så är den kontinuerlig." och samma resonemang bör gälla för vår funktion. Definitionsmängden är både intervallet x>0 och x<0. Huruvida ett "hopp" görs i x=0 borde därmed vara irrelevant eftersom funktionen inte ens är definierad där. Eller blir det en skillnad?
Jag ser att engelska Wikipedia skriver så här om funktionen f(x)=1/x: "The function f(x)=1/x is continuous on its domain (R \ {0}), but is discontinuous at x=0". https://en.wikipedia.org/wiki/Continuous_function
Säger den här definitionen att du har rätt, ja kanske… Bör jag ändra till ”Kontinuerlig i hela definitionsmängden”?
I gymnasiematten verkar dock dessa som kontinuerliga, se exempelvis https://eddler.se/lektioner/kontinuerliga-funktioner-fordjupning/ eller http://34.248.89.132:1800/index.php?title=1.5_F%C3%B6rdjupning_till_Kontinuerliga_och_diskreta_funktioner som båda tar upp detta exempel.
Återkom gärna med någon tydlig källa. Tack 🙂
Mvh Jonas
Det var svårt att skriva matte i kommentarsfältet men
En funktion f(x) är kontinuerlig i en punkt x=x0
• f(x) är definierad (x0 måste tillhöra def. mängden)
• lim f(x) (x går mot x0) existerar (funktionsvärdet måste vara lika, oavsett om man kommer från höger eller vänster mot punkten
(x0 , f(x0))
• lim f(x)= f(x0) (x går mot x0) (detta funktionsvärde är f(x0))
Så bara att den inte är definierad i 0 gör att den inte y=1/x är diskontinuerlig.
Hej igen!
Jag har nu kollat igenom flera trådar i gruppen Matematikundervisning där flera personer som arbetar med matematik på högskolenivå skriver att dessa funktioner betraktas som kontinuerliga eftersom de är detta i hela sin definitionsmängd. Ett par lyfter att det är bra att vara övertydlig om definitionsmängden, men att så länge man är det, så bör begreppet ”kontinuerlig funktion” kunna användas.
Flera skriver att ”diskontinuiter måste ligga i definitionsmängden rent formellt” och att det därmed är farligt att exempelvis kalla f(x)=1/(x-4) för diskontinuerlig. Vid hoppet bör begreppet singularitet användas istället för diskontinuitet om det ej tillhör definitionsmängden.
Jag själv kan ärligt talat för lite om detta, men jag har gjort det jag kan för att ta reda på hur det ändå ska vara… 🙂
Mvh Jonas