Linjär optimering: Största och minsta värdet i ett område
Att hitta en funktions största och minsta värde
Om du har en funktion som beror på två variabler, x och y, så kan du hitta funktionens största och minsta värde genom att undersöka hörnpunkterna i det tillåtna området i koordinatsystemet.
Funktionen brukar kallas för målfunktion.
Tre huvudsteg i linjär optimering:
- Identifiera vilka villkor som måste uppfyllas.
Skriv dessa villkor som ett system av olikheter. - Rita upp området och ta reda på hörnkordinaterna.
Enklast gör du detta i GeoGebra. - Undersök vilken kombination som ger störst värde på ”målfunktionen”.
Linjär optimering: Tillämpningar
Tydlig uppgift och strukturerad arbetsgång.
Exempelupgift:
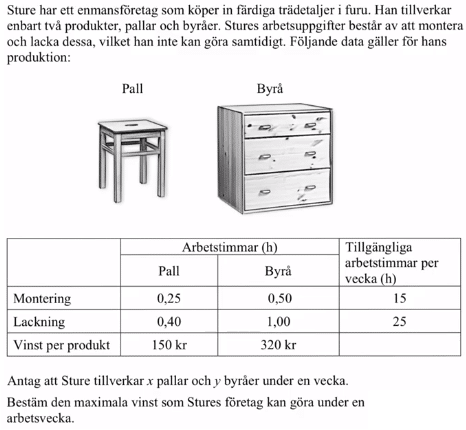
Tre huvudsteg i linjär optimering:
- Identifiera vilka villkor som måste uppfyllas.
Skriv dessa villkor som ett system av olikheter. - Rita upp området och ta reda på hörnkordinaterna.
Enklast gör du detta i GeoGebra. - Undersök vilken kombination som är mest optimal.
Detta görs med en målfunktion som i den här uppgiften beskriver totala vinsten.
Tydlig genomgång om linjär optimering (uppgiften ovan)
Liknande genomgång men med ett annat exempel
Varför återfinns största respektive minsta värdet alltid i ett av områdets hörn?
Hur gör man enklast på grafritande räknare om man inte får använda dator?
Vissa skolor säger nej till datorer under prov (2024) så det kan vara bra att veta hur man gör även på räknaren.
Att lösa uppgifter för hand, utan dator eller grafritande räknare
I de allra flesta fall bör du få använda digitala hjälpmedel för dessa uppgifter, men om du skulle sakna ett sådant behöver du bland annat kunna lösa ett ekvationssystem för hand.

Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till den!
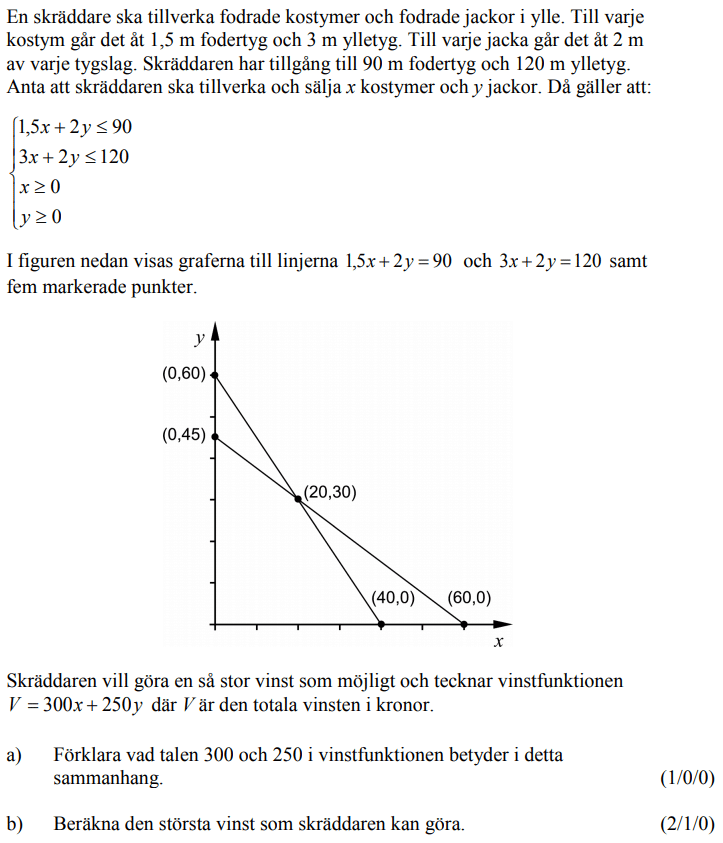
Från VT 2013 (Matematik 3b eller 3c)

Från VT 2014 (Matematik 3b)

Från HT 2013 (Matematik 3b)
