Matematik 2b och 2c
Dessa genomgångar innehåller logaritmer. Logaritmer är ett moment som enbart ingår i Matematik 2b och 2c, inte 2a.
Lösa exponentialekvationer, till exempel 2x = 12
Kortfattat: Metod för att lösa exponentialekvationer
Detta är en del av en längre genomgång. Klippet ska starta på rätt ställe.
Svårare exempel
Uppgift 4352c från Origo 2b.
För dig som är nyfiken: Olika typer av logaritmer (överkurs) och ytterligare metod att lösa exponentialekvationer.
Du behöver endast kunna Metod 1.
Exponentialekvationer, fler klipp
Snabbgenomgång: Först en potensekvation och sedan en exponentialekvation
Blandat
Att lösa exponentialekvationer (samt lite logaritmlagar)
Fler exponentialekvationer
Logaritmlagar
Mer om logaritmlagarna
Logaritmlagar: Tre uppgifter av blandad sort
Lösa exponentialekvationer utan att använda logaritmlagarna
Lösa exponentialekvationer genom omskrivning till bas 10
Ger bra förståelse!
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till denna.
Beteckningarna 2a, 2b och 2c
Beteckningarna anger vilka kurser som uppgiftens innehåll lämpar sig för.
Observera att en uppgift kan ses som relevant för en kurs, även om den inte varit med på ett nationellt prov för just den kursen. Mitt tips är att träna på alla uppgifter som har din kursbeteckning!
b-uppgiften är relevant för Matematik 2a.

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 2).

Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 2).
b-uppgiften är relevant för Matematik 2a.
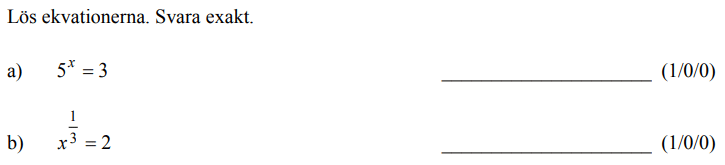
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 2).

Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 3).
b-uppgiften är relevant för Matematik 2a.

Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 2).
a- och c-uppgifterna är relevanta för Matematik 2a.
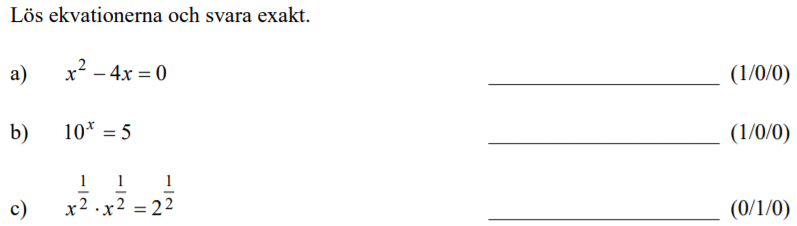
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 3).

Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 5).
a- och b-uppgiften är relevanta även för Matematik 2a.

Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 22).
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 6).

Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 7).

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 7).
a- och b-uppgifterna är relevanta för Matematik 2a.
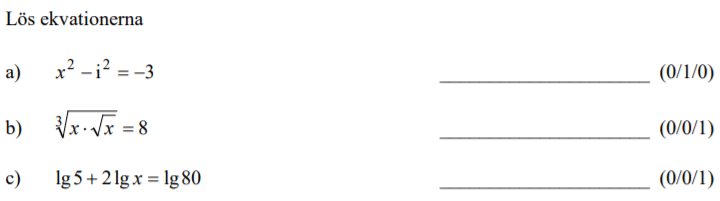
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 7).

Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 14).
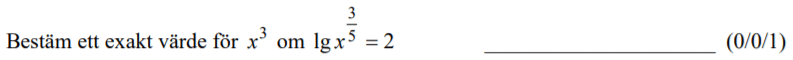
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 8).

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 8).
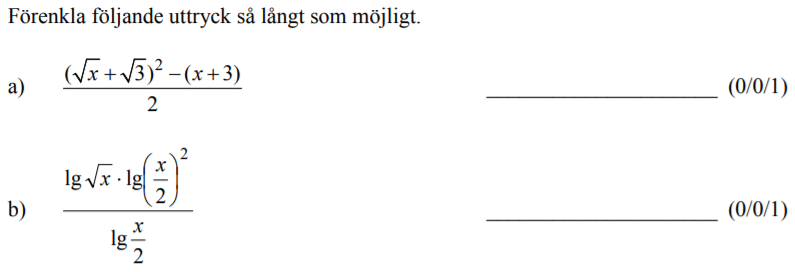
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 9).

Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 14).
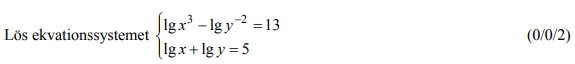
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 16).






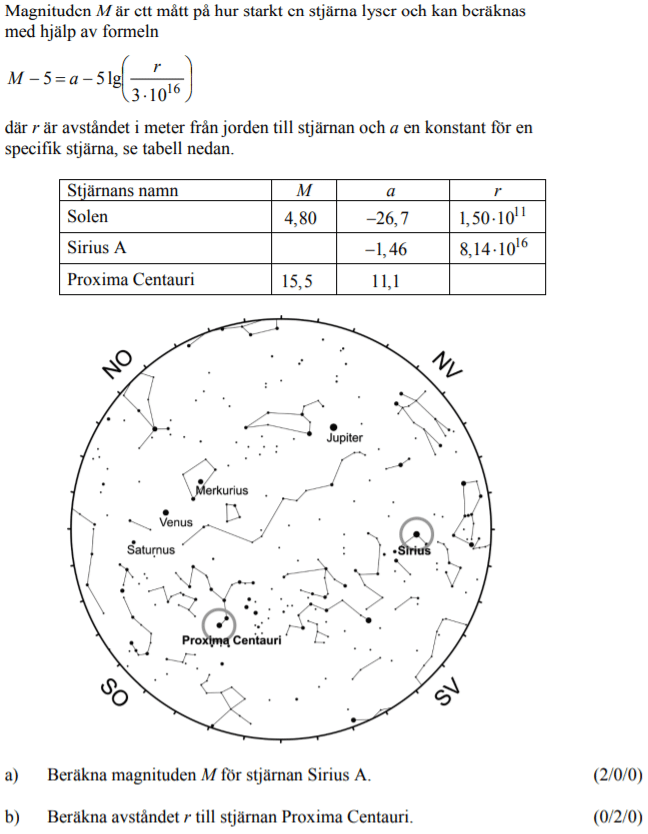
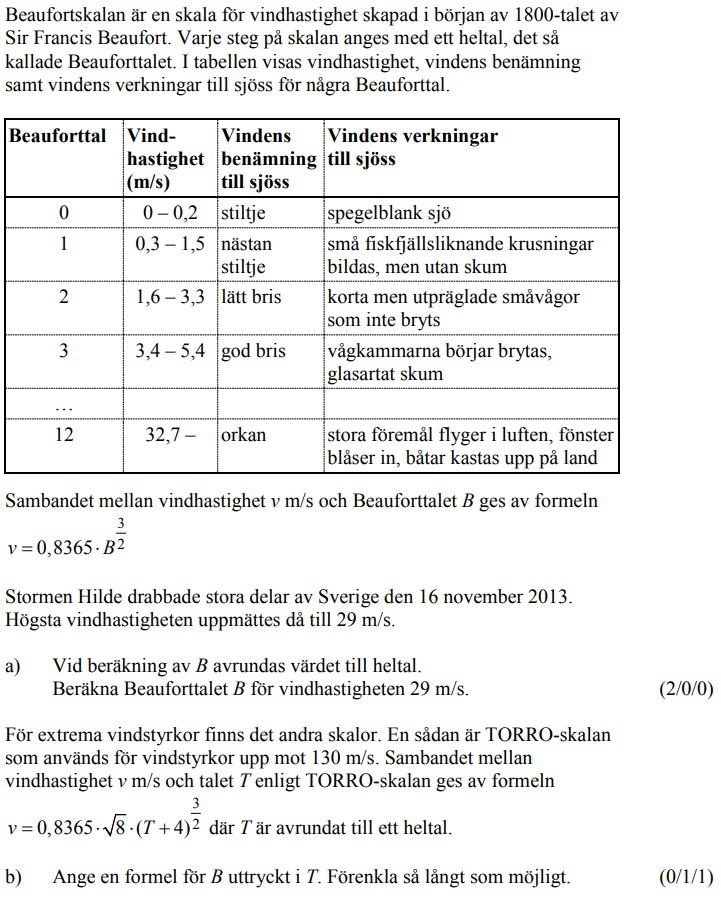
Endast för högre betyg? Fråga din lärare!
Ger bra förståelse!
Dethär förstår jag inte,ska jag göra såhär istället?
Logaritmlagarna har ju motsvarande potenslagar.
Men kan det ge högre betyg att använda potenslagarna istället? Hur bör man göra? Skillnaden blir ju bara att basen 10 står med här.
Hej! Nej jag tror att du kan hoppa över den biten. Använd logaritmreglerna tycker jag! Jag skrev dit kommentaren om högre betyg för att jag vet några lärare som vill att man ska kunna visa hur man löser exponentialekvationer genom att skriva om till bas 10 och utan att använda logaritmlagarna. Dock ska jag nog ta bort den meningen.