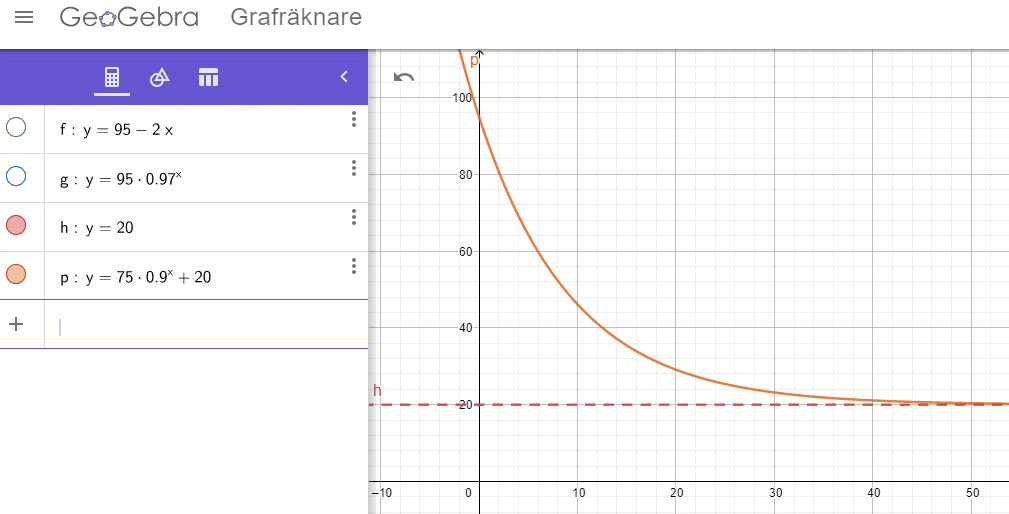
Att skriva och förstå en linjär modell, respektive en exponentiell modell över ett verklighetsbaserat exempel
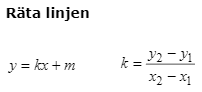
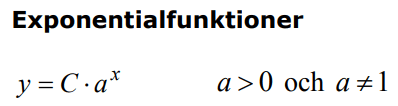
Del 1: Skriva modeller som matematiska funktioner, mm.
Del 2: Rita graf samt diskussion om modellers lämplighet/rimlighet och om de har några begränsningar.
Detta är en fortsättning från genomgången ovan. Så pausa klippet i början och läs igenom de två olika modellerna.
Uppgift att fundera över...
Rita grafen i GeoGebra till respektive modell och använd programmet till hjälp för att besvara frågorna. Länk till GeoGebra.

Förklaringar till uppgiften efter att du provat själv:
Prova själv att lösa uppgiften först, med hjälp av geogebra.
Genom att låta x anta värdet 2 och sedan beräkna y får vi följande två svar:
Modell A: 85° C.
Modell B: ca 82° C.
Enligt modell A minskar temperaturen med 5° C per timme. (Linjär förändring).
Enligt modell B minskar temperaturen med 7 % per timme. (Exponentiell förändring).
Ingen av modellerna är helt rimlig eftersom båda så småningom visar en temperatur som är lägre än 20° C, vilket inte är möjligt om detta är rumstemperaturen. Det är heller inte troligt att minskningen fortsätter att vara 5° C varje minut, när skillnaden mellan kaffets temperatur och rumstemperaturen efter några timmar inte längre är lika stor.
Det är mer rimligt med modell B än modell A, eftersom modell B gör att temperaturminskningen per timme blir mindre och mindre.
I denna modell sjunker själva temperaturskillnaden mellan kaffet och rummet med 10 % per timme. Genom att adder 20 i slutet av funktionen så kommer funktionsvärdet aldrig kunna gå under rumstemperaturen 20°, dock oändligt nära.
Skillnaden mellan de två temperaturerna är från början 75°, men det är dessa 75° som minskar för varje timme, inte hela temperaturen.
Detta bör vara den rimligaste modellen av de tre, eftersom temperaturen håller sig över rumstemperaturen, men samtidigt har en större minskning i början av förloppet än senare.
Tillämpningsuppgift om formler/samband
De sista frågorna lämpar sig väl om du siktar mot de allra högsta betygen!
Uppgift om temperaturskalorna °Celcius och °Farenheit
Två vanliga temperaturskalor är °Celsius och °Farenheit.
Följande formel kan användas för att omvandla en given temperatur mellan de två temperaturskalorna, där y är grader i Farenheit och x är grader i Celicius:
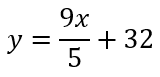
- Jonna undrar hur många °F som 20 °C motsvarar. Hjälp henne att lösa uppgiften.
- Vid hur många °F fryser vatten till is?
- Vid hur många °F är vattnets kokpunkt?
- Rita en tydlig graf över sambandet, med hjälp av de tre värden du nyss beräknat.
- Vad är funktionens k-värde, respektive m-värde?
- Jonna är i USA och har hört att det imorgon ska vara 90 °F ute. Hur många °C är detta? Läs av i grafen…
- Beräkna svaret exakt på uppgiften ovan med hjälp av en ekvation.
- Det går tydligen att både omvandla från °C till °F, men också tvärtom. Lös ut x från formeln så att du får en formel för att beräkna °C. Dubbelkolla att din omskrivna formel fungerar.
- Finns det någon temperatur där de båda temperaturskalorna visar samma värde? Motivera med beräkningar.
- Finns det någon temperatur där antal °C är exakt 20 mer än °F?