Uppgifter i Matematik 5:
Kombinatorik samt sannolikhetslära
165 uppgifter med videoförklaringar, från nationella prov, bedömningsstöd samt egna genomgångar.
Upplever du problem med att videor som du varit inne på tidigare inte startar vid rätt tidpunkt? Logga i så fall ut från ditt YouTubekonto och prova igen, alternativt öppna Vidma i inkognitoläge.
Nu kan du skriva ut uppgifterna [beta]

- Gå först in på det område du vill skriva ut.
- Välj sedan layout genom knapparna.
I utskriftsdialogrutan kan du ofta välja mellan att skriva ut till skrivare eller pdf-fil.
Livesändning från våren 2022
Exakt starttid meddelas senare, men kanske 17:30. Vi går igenom uppgifter från hela kursen, från E- till A-nivå. Sändningen kommer ligga kvar efteråt på samma länk.
Uppgifter från genomgångar.
I Matematik 5 finns inga nationella prov och dessa uppgifter är därför från mina egna genomgångar.
Ta uppgiftspoängen med en nypa salt, dessa poäng ger endast en ungefärlig bild över nivån.
Observera
Uppgifterna här speglar inte kursen på ett lika bra sätt som uppgiftssidorna för tidigare kurser. I Matematik 5 finns inget nationellt prov att låna uppgifter ifrån och uppgifterna nedan är i större grad inriktad på procedur än problemlösning, åtminstone kanske.
Ett kursprov innehåller förmodligen en högre andel problemlösningsuppgifter.
Klicka på en uppgift för att se en videoförklaring till den!

Löses utan digitala hjälpmedel. Från VT 2016 (Matematik 5).
Bedömningsanvisningar/facit (uppgift 3).

Löses utan digitala hjälpmedel. Från VT 2016 (Matematik 5).
Bedömningsanvisningar/facit (uppgift 6).

Löses utan digitala hjälpmedel.
Kommentar: Kan lösas enklare än i videoförklaringen. Se kommentar under videon.
Se korrekt svar (uppgift 15).
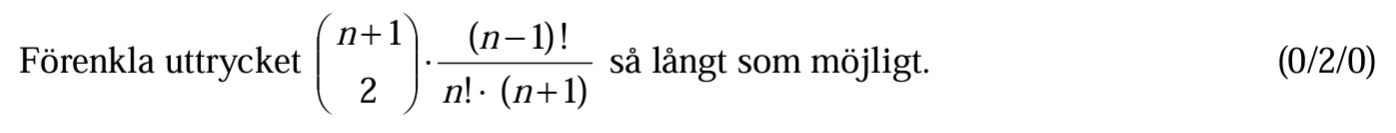
Löses utan digitala hjälpmedel. Från VT 2016 (Matematik 5).
Bedömningsanvisningar/facit (uppgift 16).

Löses utan digitala hjälpmedel. Från VT 2016 (Matematik 5).
Bedömningsanvisningar/facit (uppgift 8).









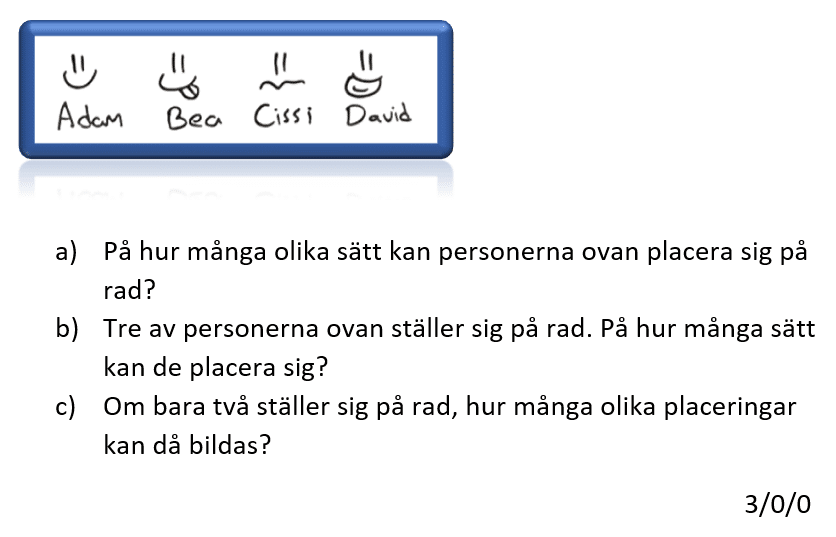











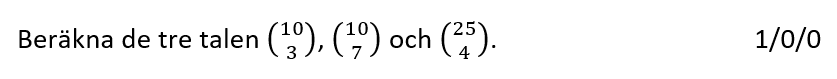
















Videogenomgången för den första E uppgiften är lite missvisande? ”Hur många vet vi helt säkert minst”. Anta jag fördelar de helt jämt ut:
3 3 3 3 3 4 4. Det finns dagar då det är 3 som fyller år. Svaret bör vara 3. För de frågar ju efter vad är det minsta möjliga antal födelsedagar om man tar hänsyn till alla dagar.
Hej! I så fall borde alltid svaret på alla de frågorna vara 0, eftersom inget säger att vi behöver fördela dem lika till att börja med.
Svaret är 4 eftersom vi vet att minst 4 kommer vara födda samma veckodag, alltså Någon av dagarna. Vi vet inte vilken dag, men vet att helt säkert så finns det Någon dag där MINST 4 av personerna är födda.
Är du med mig?..
Mvh Jonas
Hej!
I videogenomgången på fråga 35 visar du två metoder för att räkna ut antalet sätt du kan få kåk. Den ena metoden är fel med som du säger i videon, men man skulle också bara kunna multiplicera med 2 för att få samma resultat och tar då hänsyn till båda fallen.
Står det fel i facit för uppgift 35 a)? I facit så står det att man ska dela med 52ncr2. Borde det inte vara 52ncr5?
I facit på uppgift 23 b) på alternativ tror jag du har skrivit fel på beräkning men rätt svar. ska vara 5ncr3 istället för 4ncr3