Från formelbladet:
Potensreglerna - Större genomgång om alla reglerna, samt varför de fungerar
Tydlig genomgång på engelska om potensreglerna men också regler för rötter.
Tydlig genomgång på svenska om potensreglerna.
Liknande genomgång:
De enklare potensreglerna: Potenser med positiva heltalsexponenter
Liknande genomgångar:
Lite fler svåra uppgifter på slutet i denna genomgång, samt härledning av reglerna.
Ett vanligt fel som många gör!
Jämföra potenser - vilken är störst? (Svårare uppgifter)
Digital övning (extern länk)
Falköpings MatteAppar:
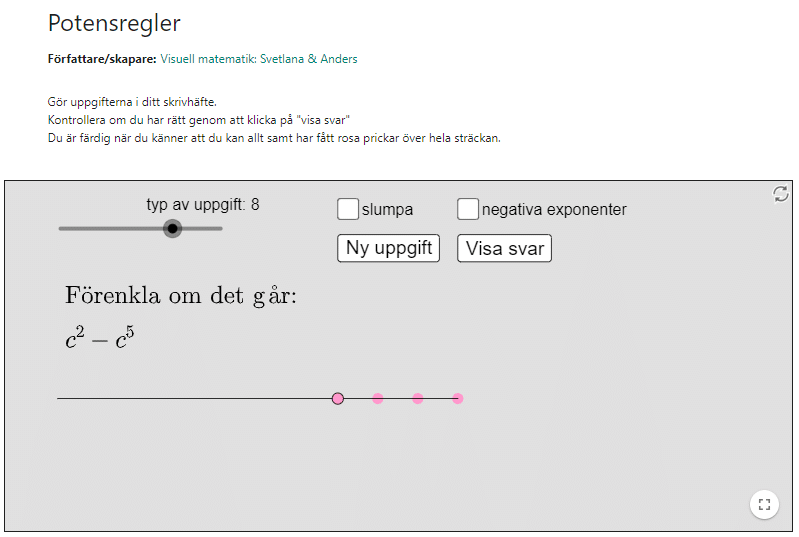
Potensregler
(Skapad av Svetlana Yushmanova och Anders Karlsson).
Bra digital övning. Du kan ändra svårighetsnivåer. Prova!
Två exempeluppgifter. En enklare (eller mellansvår) och en svår!
En riktigt svår uppgift - förklaring på engelska.
Denna är mycket svårare än vad som ingår i kursen, men är fullt lösbar med endast reglerna på formelbladet!
De lite svårare potensreglerna:
Potenser med rationella exponenter samt regler för rötter
Potenser med rationella exponenter
Rationella exponenter innebär när exponenten är ett rationellt tal, t.ex. ett bråk eller decimaltal.
Grunderna, både för heltalsexponenter, negativa exponenter och rationella exponenter
Fler exempel med rationella exponenter
På vilket sätt hör potenser och rötter (kvadratrot, kubikrot etc) ihop?
Två svåra uppgifter om att förenkla potenser med rationella exponenter
De lite svårare potensreglerna:
Potenser med negativa exponenter
Klicka på bilderna nedan för att se det viktigaste från genomgången.
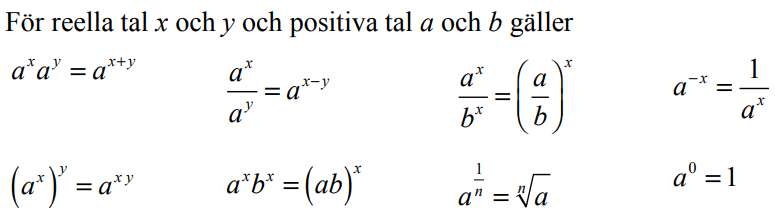
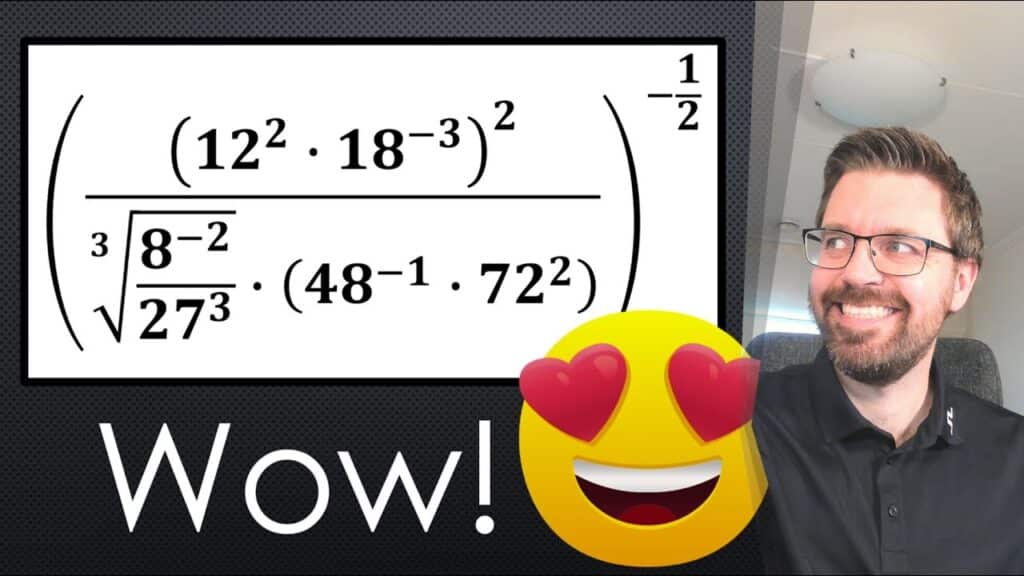
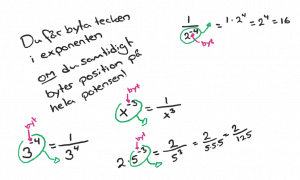
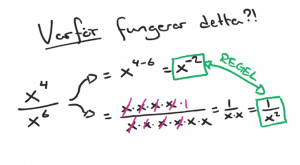
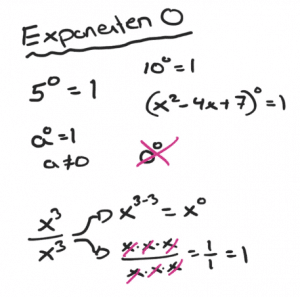
Första gången jag tycker matte är roligt
Kul Samuel att du börjar gilla det! Ibland är det inte så tokigt 🙂
Hej! Var kan jag se svaret till uppgift b? Den finns inte i videon som du hänvisat till:)
Hej Razma! Ett alldeles för sent svar, jag vet; men vilken uppgift är det du menar? I vilken video? 🙂
Hej
I videon Jämföra potenser – vilken är störst? (Svåra uppgifter) så beräknar du att 2 upphöjt med 3/2 är roten ur 8. Ska inte det istället vara roten ur två upphöjt med 3?
Hej Mikael! Båda dessa blir samma värde, testa räkna ut på räknaren. 🙂
Det spelar ingen roll om vi tar upphöjt först eller rot först och det bygger egentligen på att vi kan skriva 2^(2/3) både som (2^3)^(1/3) eller som (2^(1/3))^2.
Allmänt: a^(bc) kan skrivas a^(bc)=(a^b)^c eller a^(bc)=a^(cb)=(a^c)^b.
Du är verkligen en helt fantastisk mattelärare, du väcker ett engagemang och intresse hos mig för matte som ingen annan lärare gjort förut. Du förklarar så man verkligen förstår och märks att du brinner för ditt yrke. Den här hemsidan är min största hjälp till att klara matte 2a. Tack!