Sannolikhet: Introduktion, samt upprepade händelser (produktregeln)
Introduktion, samt produktregeln och upprepade händelser
Jag går också igenom skillnaden mellan begreppen utfall, utfallsrum och händelse, samt visar hur vi kan lösa uppgifter genom att rita utfallrummet.
Liknande genomgångar
En längre genomgång om upprepade händelser
Värd att titta på för att öka förståelsen.
Svåra uppgifter utan träddiagram - ja det går, men håll koll på vad du gör!
Uppgifter att beräkna, handlar om QuizKampen. De på slutet är riktigt svåra.
Utfallsrum
Ibland är det bra att rita upp utfallsrummet:
Relativa frekvenser - ett sätt att uppskatta sannolikheten utifrån en undersökning eller statistiska data
Kast med två tärningar, genomgång om relativa frekvenser
Genomgång om relativa frekvenser och hur det hänger ihop med den verkliga sannolikheten. Dessutom tas utfallsrum upp
Sannolikhet: Träddiagram
Mycket tydlig genomgång.
Fler genomgångar med ytterligare exempel
Stor tydlig genomgång om sannolikhet; upprepade beroende händelser och träddiagram.
En till liknande genomgång med andra exempel.
Mycket tydlig video om träddiagram
Uppgifter från tidigare nationella prov i årskurs 9 och i Matematik 1:
Klicka på en uppgift för att se en videoförklaring till denna.
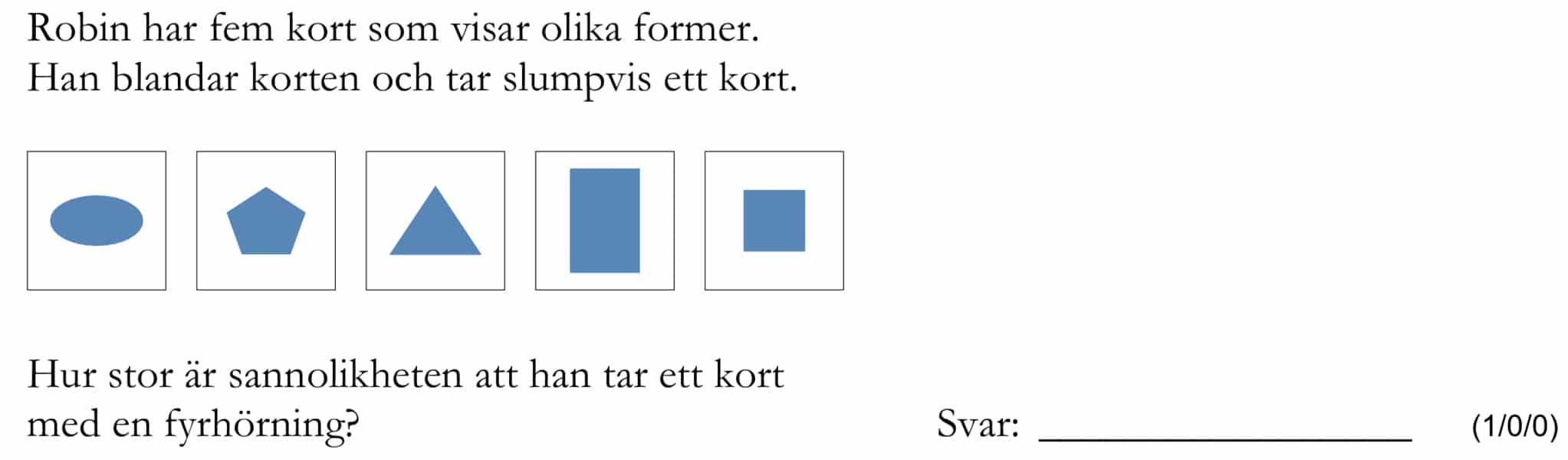
Miniräknare ej tillåten. Från vt 2013 (Matematik årskurs 9).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 7).
Miniräknare ej tillåten. Från vt 2015 (Matematik årskurs 9).
Bedömningsanvisningar/facit (uppgift 14).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 9).
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 20).
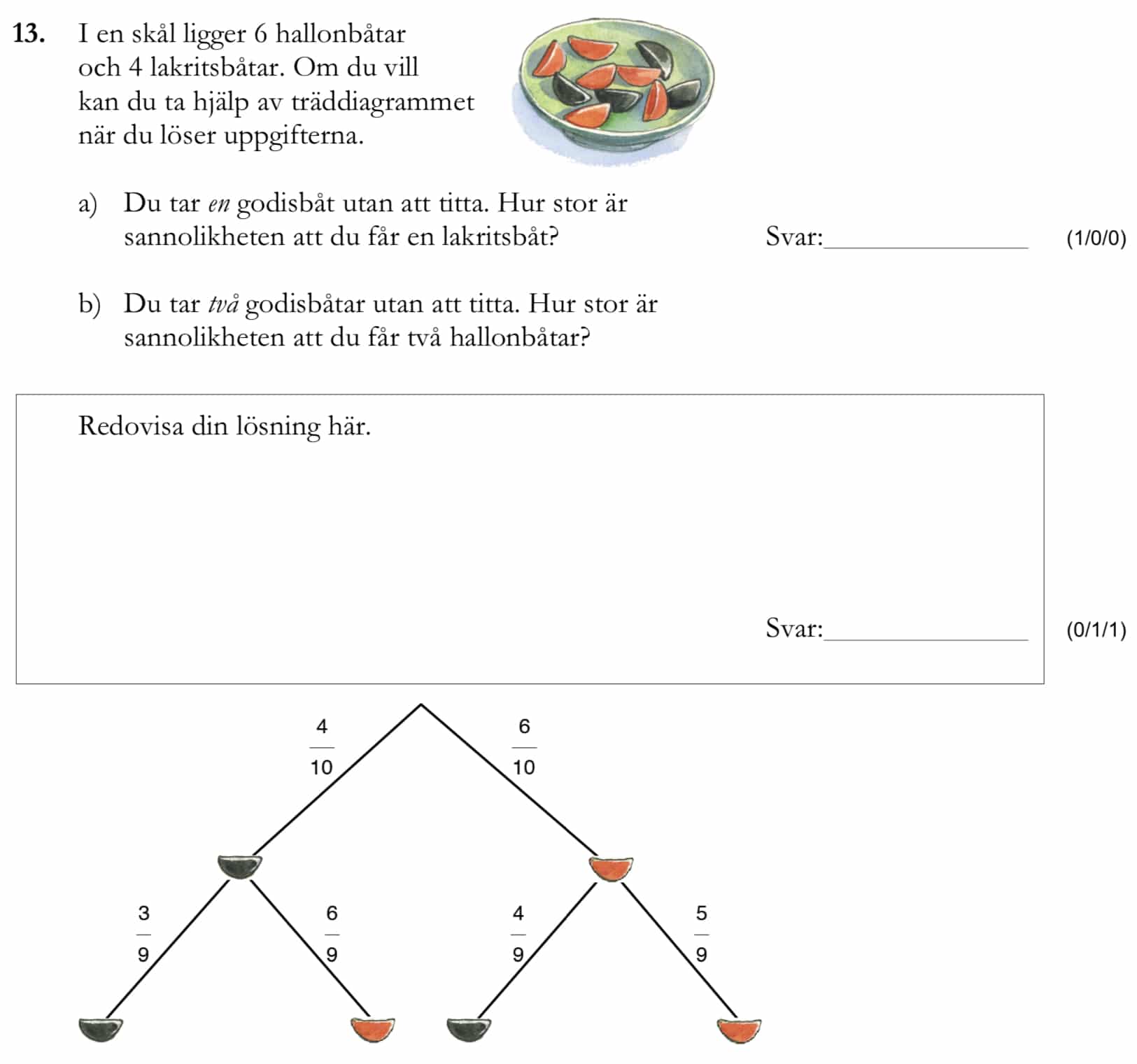
Miniräknare ej tillåten. Från vt 2014 (Matematik årskurs 9).
Bedömningsanvisningar/facit (uppgift 13).
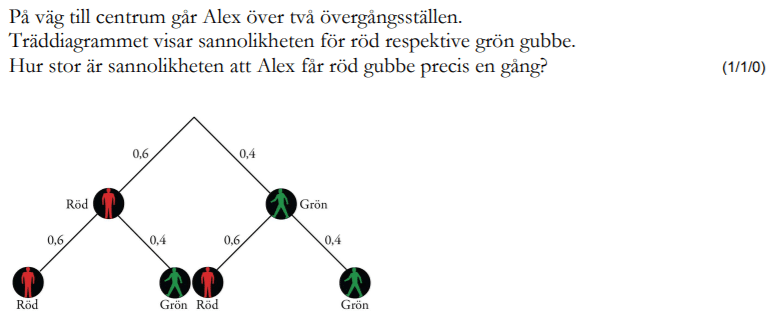
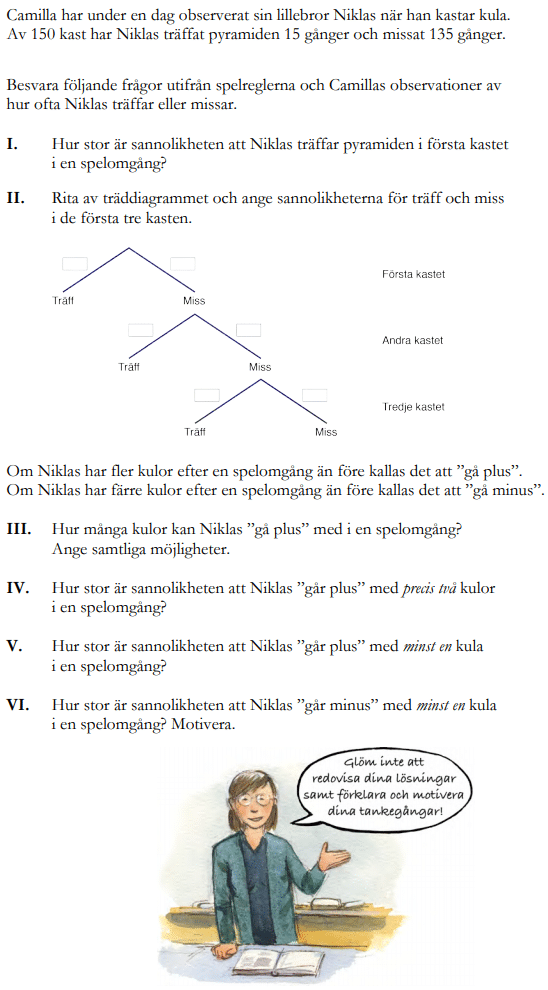
Hur löser du följande uppgiften?
P(vinst) = 4%, Vid köp av 5 lotter, vad är chansen att vinna minst ett vinst?
Hej!
Tänk så här, att lösa uppgiften är möjligt (inte bäst) genom att räkna ut sannolikheten för vart och ett av alla sätt som det går att vinna minst en vinst, och sedan addera dessa sannolikheter. Detta är jättekrångligt så därför gör vi så här istället:
”Motsatsen” (komplementhändelsen) till att vinna minst en vinst är att inte vinna någon vinst alls. Detta kan vi enkelt räkna ut:
p(ingen vinst) = p(förlust, förlust, förlust, förlust, förlust) = 0,96 * 0,96 * 0,96 * 0,96 * 0,96 = 0,96^5. Detta är ungefär lik med 0,815 = 81,5 %.
Då vet vi att sannolikheten för att minst en vinst är p(minst en vinst) = 1 – p(ingen vinst). Det är då ungefär 100 % – 81,5 % = 18,5 %.
Hängde du med? 🙂
Hej Jonas! Jag trodde inte att jag ska förstå sannolikhetenslära men dina videor gav mig oerhört mycket! Nu kan jag lösa krångliga uppgifter och denna lång uppgift är ganska roligt! Tusen tack!
Hej Radomir! Vad roligt att höra, jag blir verkligen glad! Hoppas det går bra för dig med matten även framöver! Lycka till 🙂
Mvh Jonas
Hur löser man uppgiften med trafiken ljusen (uppgift 17 nationella provet) Om P ( ingen grön). Skulle uppskatta om du kunde svara för jag har inte riktigt förstått hur man löser den.