Skala: förstoring och förminskning
Längre liknande genomgång, med fler exempeluppgifter.
Längdskala, areaskala, volymskala
På formelbladet:
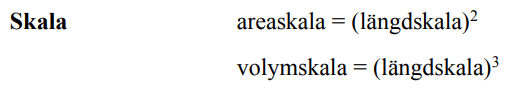
Exempel.
Om längdskalan (vanliga skalan) är 1 : 10, så kan vi räkna ut areaskalan och volymskalan så här:
Areaskalan blir 1 : 100 (uträkning: 1·1=1 och 10·10=100). Arean i en figur förminskas alltså till en hundradel om figurens längder minskas till en tiondel.
Volymskalan blir 1 : 1000 (Uträkning: 1·1·1=1 och 10·10·10=1000). Volymen förminskas alltså till en tusendel om alla längder minskas till en tiondel.
Svårare exempel.
Om längdskalan (vanliga skalan) är 2 : 3, så kan vi räkna ut areaskalan och volymskalan så här:
Areaskalan blir 4 : 9 (uträkning: 2·2=4 och 3·3=9). Arean i en figur förminskas alltså till en fyra niondelar om figurens längder minskas till två tredjedelar.
Volymskalan blir 8 : 27 (Uträkning: 2·2·2=8 och 3·3·3=27). Volymen förminskas alltså till åtta tjugosjundedelar om alla längder minskas till två tredjedelar.
Hur fungerar skala om det gäller area eller volym?
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till denna.
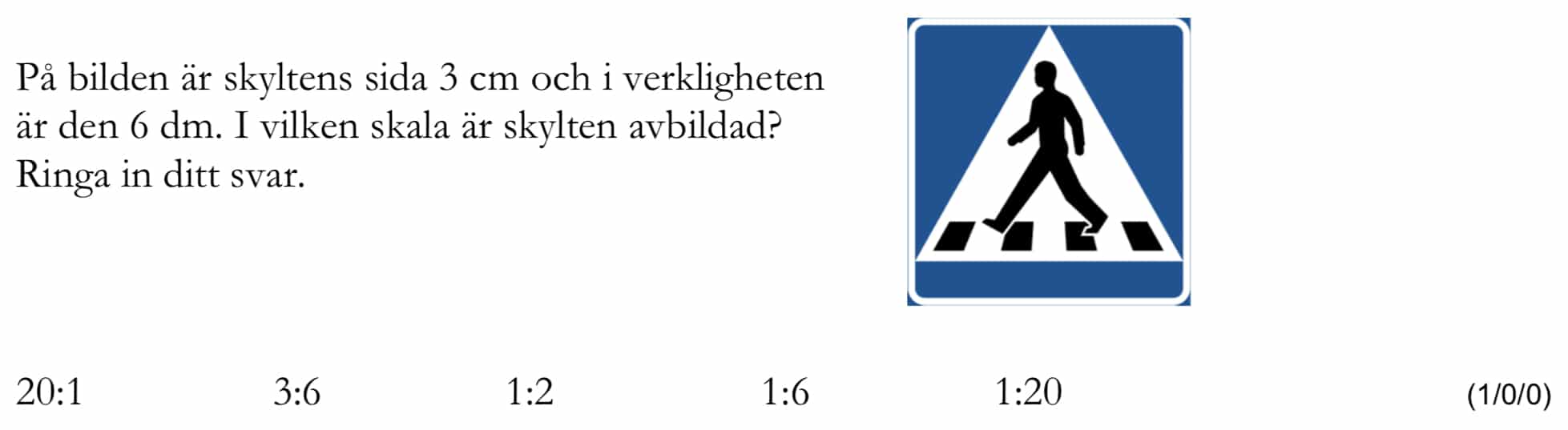
Miniräknare ej tillåten. Från vt 2015 (Matematik årskurs 9).
Bedömningsanvisningar/facit (uppgift 3).
Du kan inte mäta här på skärmen. Starta videolösningen så får du hjälp med måtten!
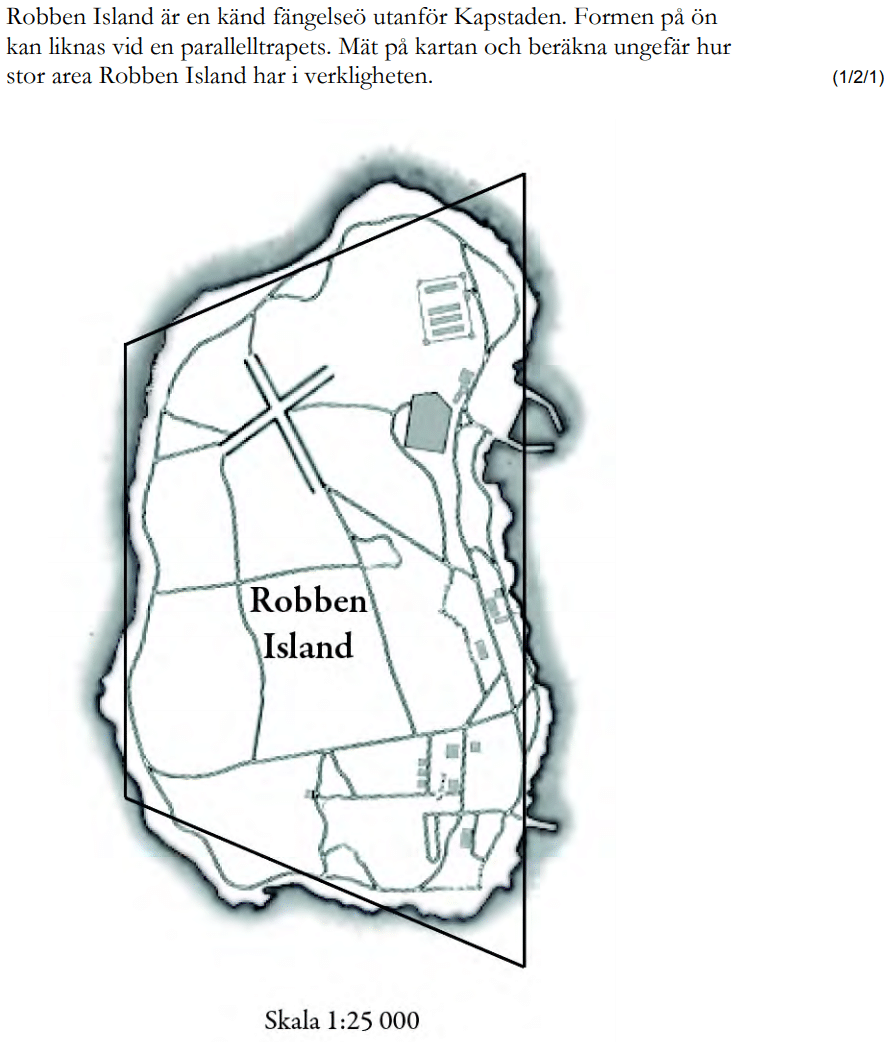
Från vt 2013 (Matematik årskurs 9).
Bedömningsanvisningar/facit (uppgift 27).



