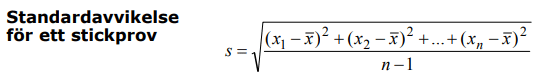Vad är standardavvikelse och normalfördelning?
Längre genomgång som ger en bra förståelse för begreppen och hur vi använder Geogebra för att beräkna standardavvikelse och lösa uppgifter med normalfördelning.
Jag tar inte upp hur man beräknar standardavvikelse för hand, det ingår inte längre i Matematik 2-kurserna.
Första 32 minuterna är viktiga och rekommenderas att se. Luta dig tillbaka!
Dra i glidarna och se hur normalfördelningskurvan ändras!
Liknande genomgångar
Jag beräknar inte standardavvikelsen i dessa två klipp nedan.
Längre genomgång som ger en bra förståelse för vad standardavvikelse och normalfördelning är:
Liknande genomgång som tar upp normalfördelning och standardavvikelse lite mer kortfattat:
Att beräkna standardavvikelsen
Standardavvikelse för ett stickprov - när alla värden inte mätts
Alternativ 1: Med digitala verktyg (räknare eller GeoGebra)
Länk till annan sida på Vidma:
Alternativ 2: För hand
Att beräkna standardavvikelse för hand ingår inte längre i Matematik 2. Rekommenderas ej!
s = standardavvikelsen för ett stickprov (stickprov innebär att de värden som mätts endast är en del av samtliga värden).
= medelvärdet för stickprovet
x1 = första värdet
x2 = andra värdet (osv.)
xn = sista värdet (värde nummer n)
n = antal mätvärden
= medelvärdet för stickprovetOlika beteckningar används i formeln ovan och i kurvan på formelbladet eftersom formeln ovan endast ger en ”uppskattning” av standardavvikelsen och medelvärdet baserat på de värden som faktiskt mätts.
Värdet s som genereras i formeln kommer alltså inte stämma överens med kurvan helt exakt eftersom alla värden ej mätts. Formeln ovan bygger ju på att endast ett stickprov har genomförts.
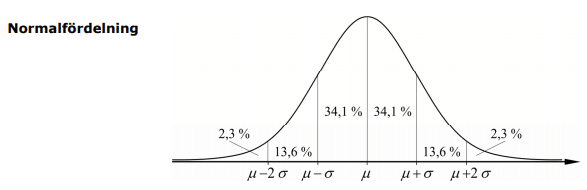
Beräkningar med normalfördelning
Hur vi kan förutsäga att samtliga värden sannolikt kommer fördela sig om alla värden skulle mätas
Alternativ 1: Med digitala verktyg (räknare eller GeoGebra)
Länk till annan sida på Vidma:
Alternativ 2: För hand med hjälp av formelbladet
μ = medelvärdet för samtliga värden (”hela populationen”).
σ = standardavvikelsen för samtliga värden (”hela populationen”).
Vad är det för skillnad på att undersöka "hela populationen" (totalundersökning) eller att undersöka ett stickprov?
... och varför används flera olika beteckningar för standardavvikelse och medelvärde?
s = standardavvikelsen för ett stickprov (stickprov innebär att de värden som mätts endast är en del av samtliga värden).
σ = standardavvikelsen för samtliga värden (”hela populationen”).
= medelvärdet för ett stickprov.
μ = medelvärdet för samtliga värden (”hela populationen”).
Lång men tydlig genomgång om standardavvikelse där jag ockå beräknar standardavvikelsen för hand.
Luta dig tillbaka i soffan en stund…