Andragradsfunktioner och dess graf
Nollställen, symmetrilinje, extrempunkt (minimipunkt, maximipunkt) mm.
"Fusklapp" att anteckna på insidan av matteblocket...
Under bilden finns en genomgång där jag berättar om bilden, tillsammans med ett exempel.
Genomgång med exempeluppgift
Nollställen, symmetrilinje, extrempunkt (minimipunkt, maximipunkt) mm.
Liknande genomgång
Längre genomgång som täcker in det allra mesta!
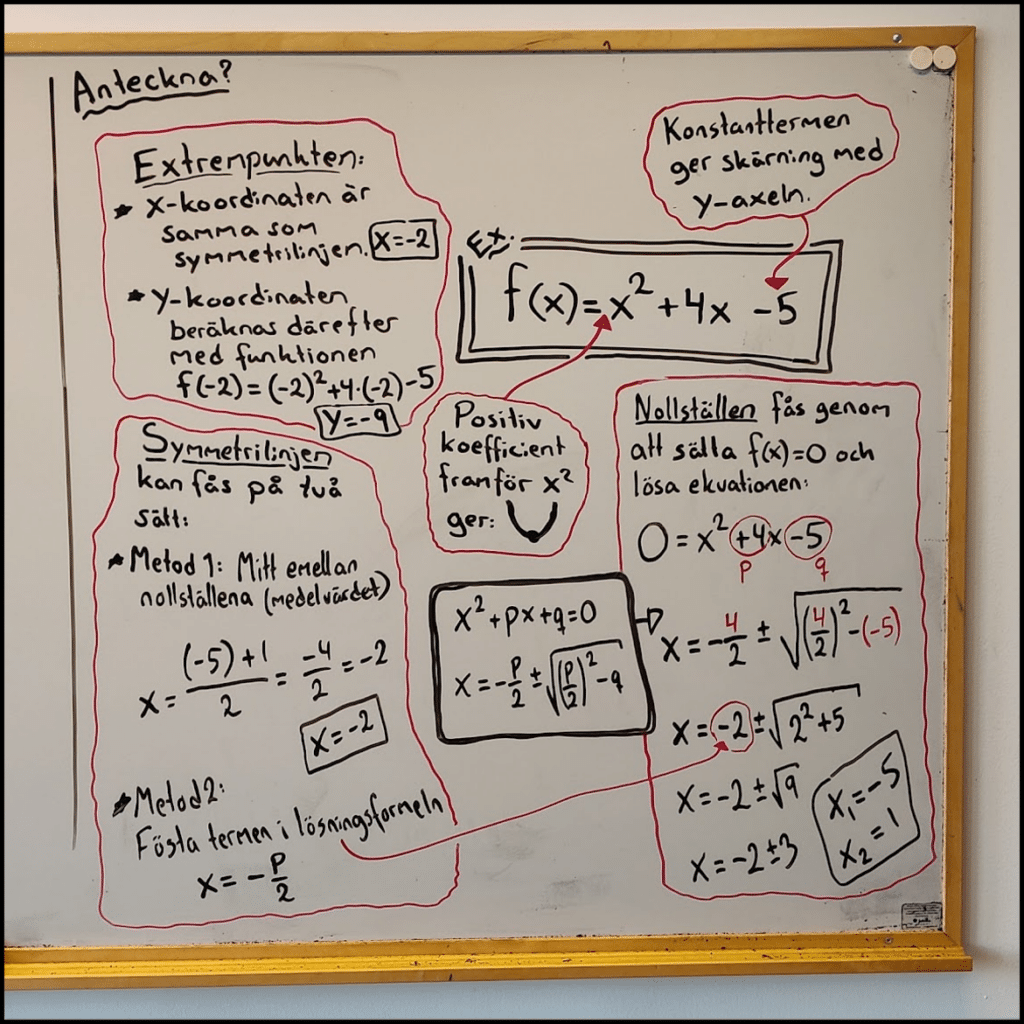
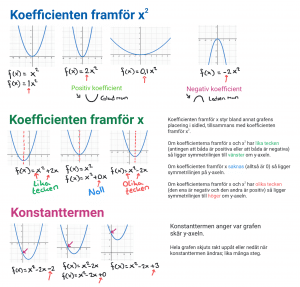
Karaktär (utseende), skärning med y-axeln, nollställen (skärning med x-axeln), symmetrilinje, extrempunkt (minimipunkt, maximipunkt)
Gör nu uppgifterna nedan - våga inte hoppa över det!
En exempeluppgift till - gör denna själv!
Prova räkna denna själv och jämför med mina uträkningar!
Och ytterligare en exempeluppgift till - gör den med!
Prova räkna denna själv och jämför med mina uträkningar!
Två liknande genomgångar som täcker in det viktigaste.
Del 1
- Hur vet vi om grafen har en minimipunkt eller maximipunkt?
- Hur beräknas nollställen och symmetrilinje?
Del 2
Exempeluppgift om att beräkna symmetrilinjen, det största eller minsta värdet, samt skissa grafen.
Sammanfattat:
Karaktär (utseende), skärning med y-axeln, nollställen, symmetrilinje, extrempunkt (minimipunkt, maximipunkt)
En till genomgång
Liknande genomgång som tar upp hur du beräknar startvärde, nollställen, symmetrilinje, extrempunkt (minimipunkt, maximipunkt)
En till genomgång med mer fokus på hur grafen ser ut.
Fortsätt gärna till delen med tillämpningar, uppgifterna där handlar till oerhört stor del om detta!
Svår A-uppgift
Finns det något värde på a som gör att funktionen f(x) = x2 + 2ax har sin extrempunkt på linjen y = -3x + 5 ?
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring till denna.
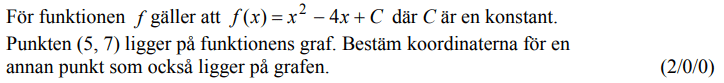
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Många E, C- och A-uppgifter:
Uppgifter för Matematik 2 sorterade efter område - med videoförklaringar!
E-nivå
C-nivå
A-nivå (extra många)
Du e bättre än min matte lärare!
Kul att du gillar genomgångarna 🙂
tack för hemsidan. Jag tror att du råkade beräkna extremvärdet fel.
f(x) = -x^2 + 8x – 12
om vi sätter symetrilinjens värde som var 4 i funktionen så får vi
f(4) = -4^2 + 8(4) -12
f(4) = 16 + 32 – 12 = 36
största värdet blir 36 och inte 4 🙂
räknade svaret med miniräknaren. det blir 4 . du har rätt. fast en sak. i min värld så betyder -4^2 samma sak som -4 gånger -4 . hur kommer det sig att -4^2 = -16 men -4gånger -4 blir +16?
Hej! Vad bra att du skriver när du ser något som kanske är fel, även om det denna gång inte var det!
När det står -4^2 så gäller tvåan bara för talet 4. Detta beror på prioriteringsreglerna och att upphöjt alltid räknas före subtraktion. Det betyder alltså -4•4=-16.
Om det däremot står x^2 och du får reda på att x=-4 så blir det annorlunda, då måste vi skriva med parentes för att visa att hela talet -4 ska vara upphöjt med 2. (-4)^2=16.
Hänger du med? 🙂
Mvh Jonas
Hej Jonas!
På första genomgången ”Karaktär (utseende), skärning med y-axeln, nollställen, symmetrilinje, extrempunkt (minimipunkt, maximipunkt)” är ljudet avstängt under tiden 6.09 till 9.26 så du vet om det, men man väldigt bra genomgång ändå!!
Oj märkte precis att du skrev det på videon:), mitt fel
Hej!
Ja, jag upptäckte det långt efter att jag spelat in klippet tyvärr. Men kul att du gillar genomgången ändå. 🙂 Ska skriva ut det tydligare på sidan att ljudet är borta.
Lycka till med matten! 🙂
Mvh Jonas
hur ska man tänka om det står ex ”bestäm f(-2)” eller ”bestäm x om f(x-4) =-2” och sen är de en bild av en graf mvh förrvirrad vuxen som läser in högskolebehörighet
Hej! Jag hade missat din kommentar, har du fått koll? 🙂 Om inte så kanske de hittar någon uppgift här som är lik den du har, kolla videoförklaringen i så fall. Återkom om du fortfarande funderar sen. https://vidma.se/np1funktioner/
Mvh Jonas
Rösten på videon försvinner vid 6:12 min
Hej! Ja, tyvärr är den borta en liten stund, men kommer sedan tillbaka. 🙂
(Sent svar, men någon annan kanske läser).
Jag älskar dina videor, mycket väl förklarade och tydliga exempel. men jag önskar bara att du hade lite mer utrymme när du skrev ut stegen så att det är lättare att se och följa utan att allt flyter ihop.
Hej Jonas! Du räddar verkligen mig just nu. Jag har inte pluggat matte sedan gymnasiet (10 år sedan) och haft så kallat ”matte-trauma”. Behöver lära mig matte på nytt nu och har varit så orolig att det skulle kännas jobbigt och tråkigt som jag minns att det gjorde under skoltiden. Det visade sig att det verkligen beror på vilken lärare man har, du har fått matte att inte bara kännas enkelt utan också väldigt roligt! Tack vare dig börjar jag känna mig självsäker på matte för första gången. Tusen, tusen tack för den här hemsidan och allt ditt jobb!