Sammanfattning över detta område
Detta klipp är bra som sammanfattning, men har du inte hört talas om talet e eller logaritmen ln tidigare så bör du börja med genomgångarna nedanför.
Deriveringsregler, del 3: Exponentialfunktioner, talet e och den naturliga logaritmen ln
Hur vi deriverar f(x) =ex och f(x) = ekx samt vad talet e är.
Liknande video:
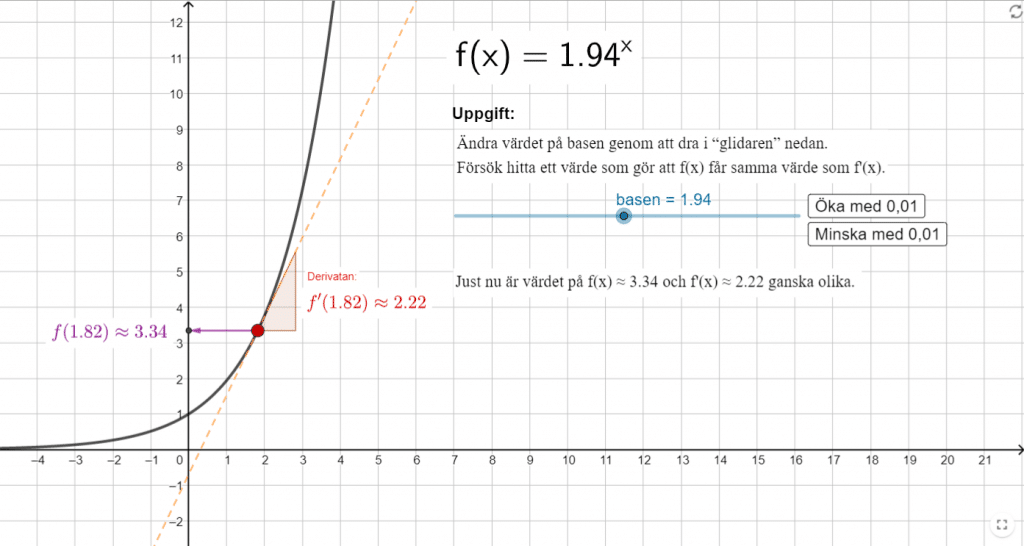
Labb: Testa själv att hitta talet e.
Här nedan kan du prova själv och se om du kan hitta talet e. Det är alltså det värde på basen som gör att y-värdet blir detsamma som derivatan, alltså att f(x) = f'(x). TESTA!
Kortare genomgång!
Att derivera f(x) = ekx och f(x) = akx
Långsam och metodeisk med bara det viktigaste
Liknande genomgång: att derivera f(x) = akx
Faktarutor
Faktaruta
När du deriverar f(x) = ex så blir derivatan precis likadan, nämligen f'(x) = ex.
Talet e är ungefär 2,718 och just det talet har egenskapen ovan.
Detta innebär att i precis varje punkt på grafen till f(x) = ex så är y-värdet f(x) detsamma som lutningen f'(x). Det är bara talet e som har denna egenskap.
Faktaruta
När du deriverar f(x) = ekx så blir derivatan f'(x) = k · ekx.
Exempel: När du deriverar f(x) = e2x så blir derivatan f'(x) = 2e2x.
Du ska alltså kopiera ner koefficienten som står framför x. Ingenting ändras i exponenten.
Faktaruta
När du deriverar f(x) = akx så blir derivatan f'(x) = k · akx · ln(a).
Exempel: När du deriverar f(x) = 42x så blir derivatan f'(x) = 2 · 42x · ln(4).
Du ska alltså kopiera ner koefficienten som står framför x. Dessutom ska du multiplicera med ln för exponentens bas.
Övrigt och en aning blandat
För dig som tycker sånt här är intressant:
Härledning av talet e
Talet e är ungefär 2,781, men kan också beskrivas med ett gränsvärde – som kan härledas genom derivatans definition. Nedan syns en härledning av varför talet e blir just detta gränsvärde.
En annan härledning av varför e är just ungefär 2,72.
Innefattar derivatans definition och numerisk digital beräkning av gränsvärde.