Repeterande genomgång om alla tre metoderna:
-Additionsmetoden
-Substitutionsmetoden
-Grafisk lösning
Bra om du vill ha genomgång på ALLA metoderna och orkar hålla fokus 🙂
OBS: Har du aldrig arbetat med detta förut så börja titta på genomgångarna längre ner!
Hur du löser ett ekvationssystem algebraiskt
- Skapa en ekvation som endast innehåller en sorts variabel (tex bara x eller bara y).
- Lös ekvationen. Då vet du värdet på ena variabeln.
- Räkna ut den andra variabeln.
Metod 1: Additionsmetoden
Genomgång om additionsmetoden
Liknande genomgångar
Metod 2: Substitutionsmetoden
Genomgång om substitutionsmetoden
Fler liknande genomgångar om substitutionsmetoden
Prova gärna att lösa uppgifterna själv först och använd genomgången som ett sätt att se om du fått rätt och vad du eventuellt kunde ha gjort annorlunda.
Svårare uppgifter
Uppgifter där substitutionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.
Denna uppgift inkluderar kunskaper om logaritmer (senare i kursen)
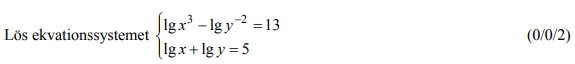
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 16).

Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 16).

Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 12).
Uppgifter där additionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.
Ytterligare uppgifter
Uppgifter där både substitutionsmetoden och additionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.
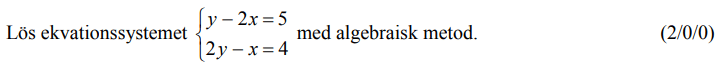
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 11).
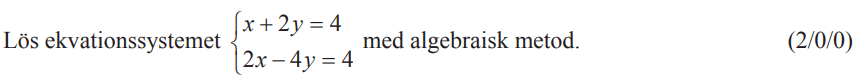
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 12).
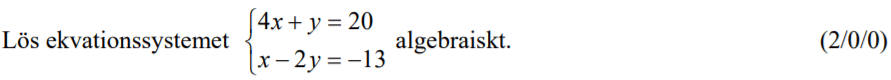
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 12).

Y-2x=5
2y-x=4
x=-2
Hej!
Jag vill bara ta tillfället att ge dig ett stort TACK för dina ansträngningar på denna sida! Jag är en 43 årig trebarnsmamma som inte läst matte sedan gymnasiet och som då tyckte matte var nästan obegripligt svårt, men som nu läser Ma2a för att få särskild behörighet till en universitetsutbildning. Tack vare dig har matte ÄNTLIGEN blivit logiskt och nästan lite kul! =) TACK!
Hej Maria och vad roligt att du skriver! Tack så väldigt mycket för de fina orden, jag är glad att kunna hjälpa till på vägen 🙂 Hoppas du känner att kursen går bra och att det fortsätter att vara en aning kul ibland! 😀 Lycka till framåt!
Mvh Jonas