Uppgifter i Matematik 1:
Formler
Välj kurs och innehåll:
Matematik 1a
Välj område nedan.
För Matematik 1a kan olika delar av detta innehåll ingår beroende på vilket program eleven läser. Uppgifterna på ett nationellt prov brukar enbart testa de delar som är gemensamma för alla (vilket är det allra mesta av detta innehåll).
Ungefär 300 uppgifter med videoförklaringar, varav de allra flesta från tidigare nationella prov.
Jag ska räkna noggrannare vid tillfälle!
Uppgifter från nationella prov och från genomgångar.
Många av uppgifterna är från tidigare nationella prov, men det finns också ett antal uppgifter från mina egna genomgångar.
Uppgifterna från de nationella proven har tydliga bedömningsanvisningar, medan uppgifterna från mina egna genomgångar saknar detta än så länge. Dock finns videoförklaring till samtliga uppgifter där jag alltid berättar rätt svar.
Visst innehåll har flyttat mellan kurserna
År 2021 förändrades kursplanerna och visst innehåll har flyttat mellan de olika kurserna. Exempelvis tillhör räta linjens ekvation numera Matematik 1b och 1c istället för Matematik 2b och 2c. Många av uppgifterna i det området kommer därför från tidigare Matematik 2-prov. Också statistikområdet är till stora delar nytt.
Klicka på en uppgift för att se en videoförklaring till den!
Matematik 1b
Välj område nedan.
Ungefär 300 uppgifter med videoförklaringar, varav de allra flesta från tidigare nationella prov.
Jag ska räkna noggrannare vid tillfälle!
Uppgifter från nationella prov och från genomgångar.
Många av uppgifterna är från tidigare nationella prov, men det finns också ett antal uppgifter från mina egna genomgångar.
Uppgifterna från de nationella proven har tydliga bedömningsanvisningar, medan uppgifterna från mina egna genomgångar saknar detta än så länge. Dock finns videoförklaring till samtliga uppgifter där jag alltid berättar rätt svar.
Visst innehåll har flyttat mellan kurserna
År 2021 förändrades kursplanerna och visst innehåll har flyttat mellan de olika kurserna. Exempelvis tillhör räta linjens ekvation numera Matematik 1b och 1c istället för Matematik 2b och 2c. Många av uppgifterna i det området kommer därför från tidigare Matematik 2-prov. Också statistikområdet är till stora delar nytt.
Klicka på en uppgift för att se en videoförklaring till den!
Matematik 1c
Välj område nedan.
Ungefär 300 uppgifter med videoförklaringar, varav de allra flesta från tidigare nationella prov.
Jag ska räkna noggrannare vid tillfälle!
Uppgifter från nationella prov och från genomgångar.
Många av uppgifterna är från tidigare nationella prov, men det finns också ett antal uppgifter från mina egna genomgångar.
Uppgifterna från de nationella proven har tydliga bedömningsanvisningar, medan uppgifterna från mina egna genomgångar saknar detta än så länge. Dock finns videoförklaring till samtliga uppgifter där jag alltid berättar rätt svar.
Visst innehåll har flyttat mellan kurserna
År 2021 förändrades kursplanerna och visst innehåll har flyttat mellan de olika kurserna. Exempelvis tillhör räta linjens ekvation numera Matematik 1b och 1c istället för Matematik 2b och 2c. Många av uppgifterna i det området kommer därför från tidigare Matematik 2-prov. Också statistikområdet är till stora delar nytt.
Klicka på en uppgift för att se en videoförklaring till den!
Upplever du problem med att videor som du varit inne på tidigare inte startar vid rätt tidpunkt? Logga i så fall ut från ditt YouTubekonto och prova igen, alternativt öppna Vidma i inkognitoläge.
Nu kan du skriva ut uppgifterna [beta]
- Gå först in på det område du vill skriva ut.
- Välj sedan layout genom knapparna.
I utskriftsdialogrutan kan du ofta välja mellan att skriva ut till skrivare eller pdf-fil.
Här finns genomgångar om detta:
Klicka på en uppgift för att se en videoförklaring till denna.
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 5).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 1).
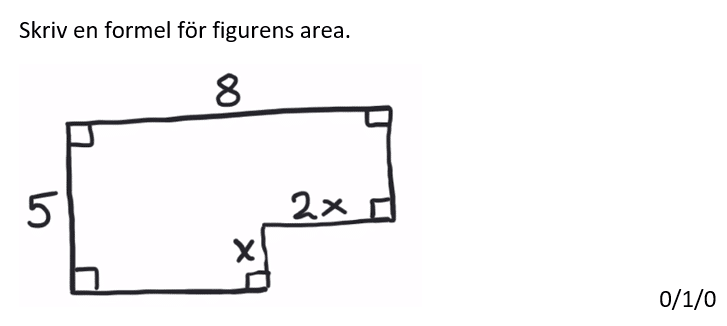
Från egen genomgång.
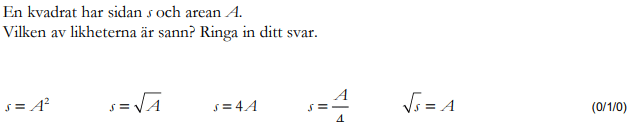
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 9).
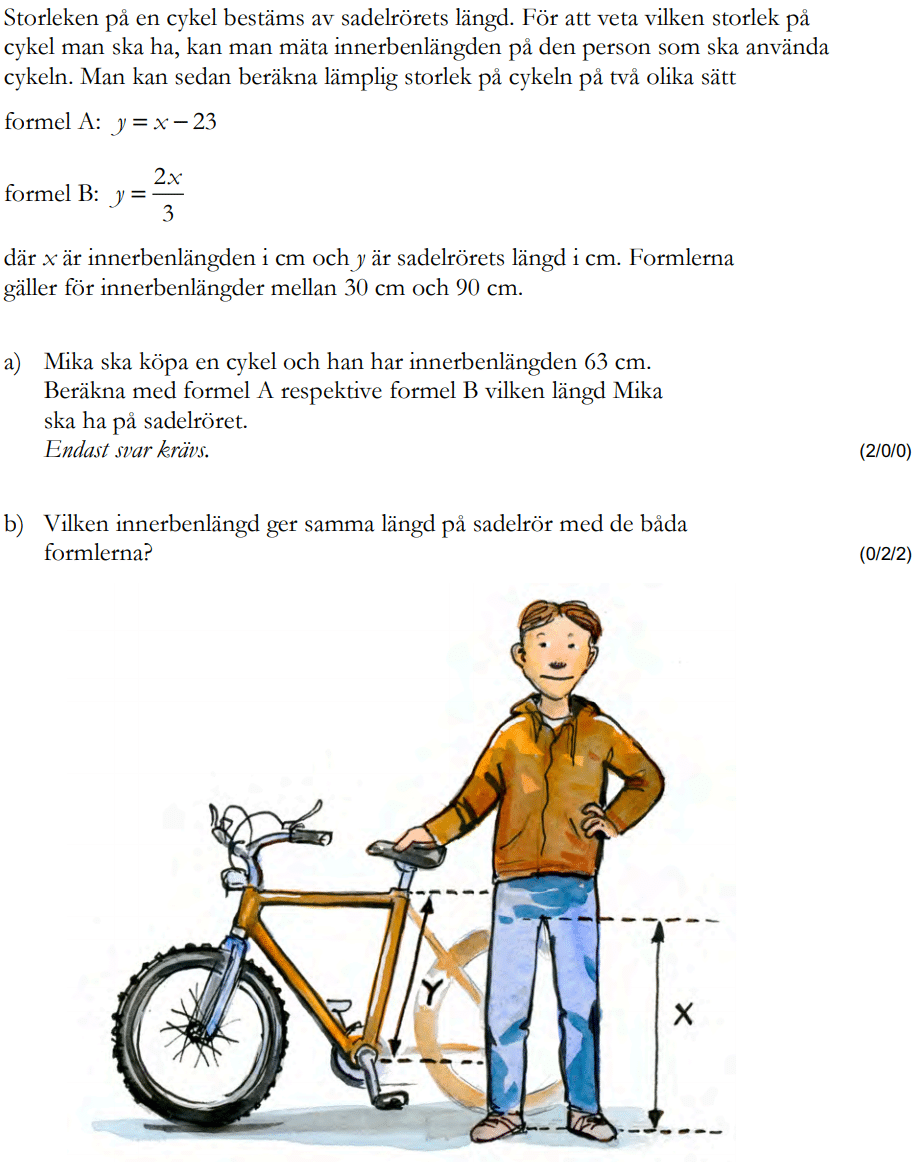
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 22).
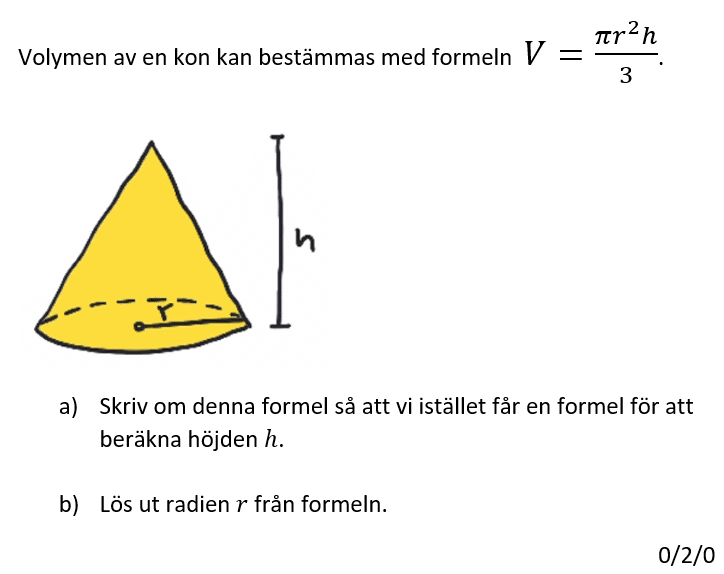
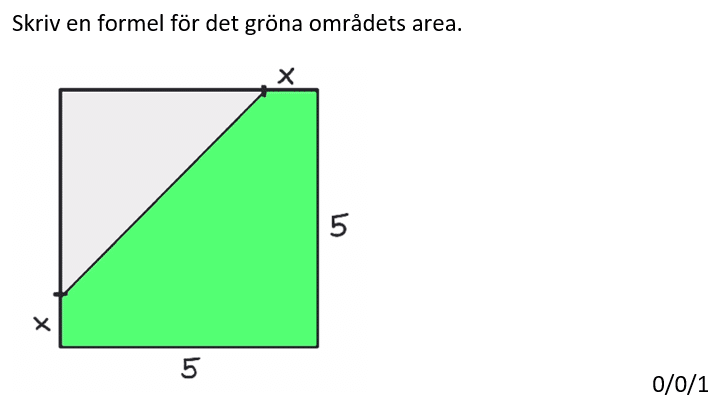
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 11).
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 10).
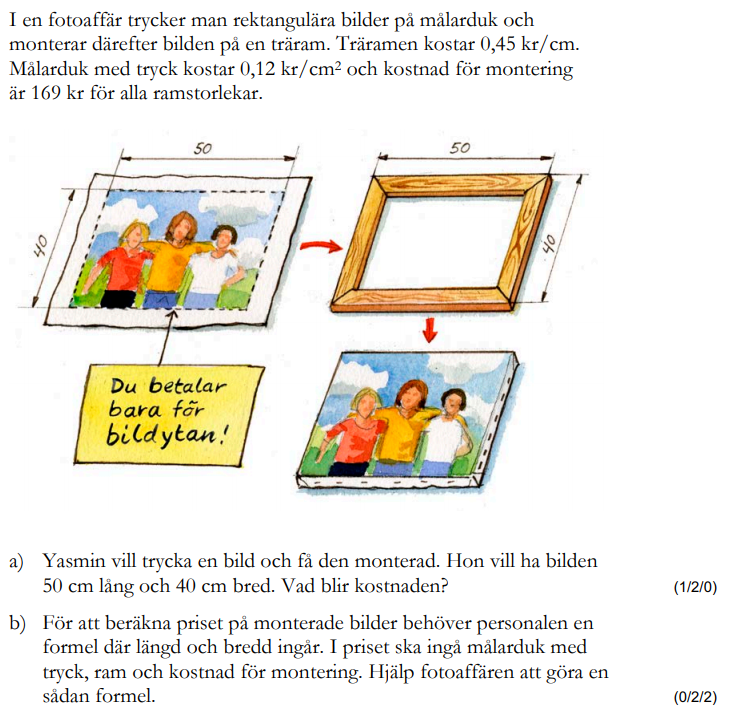
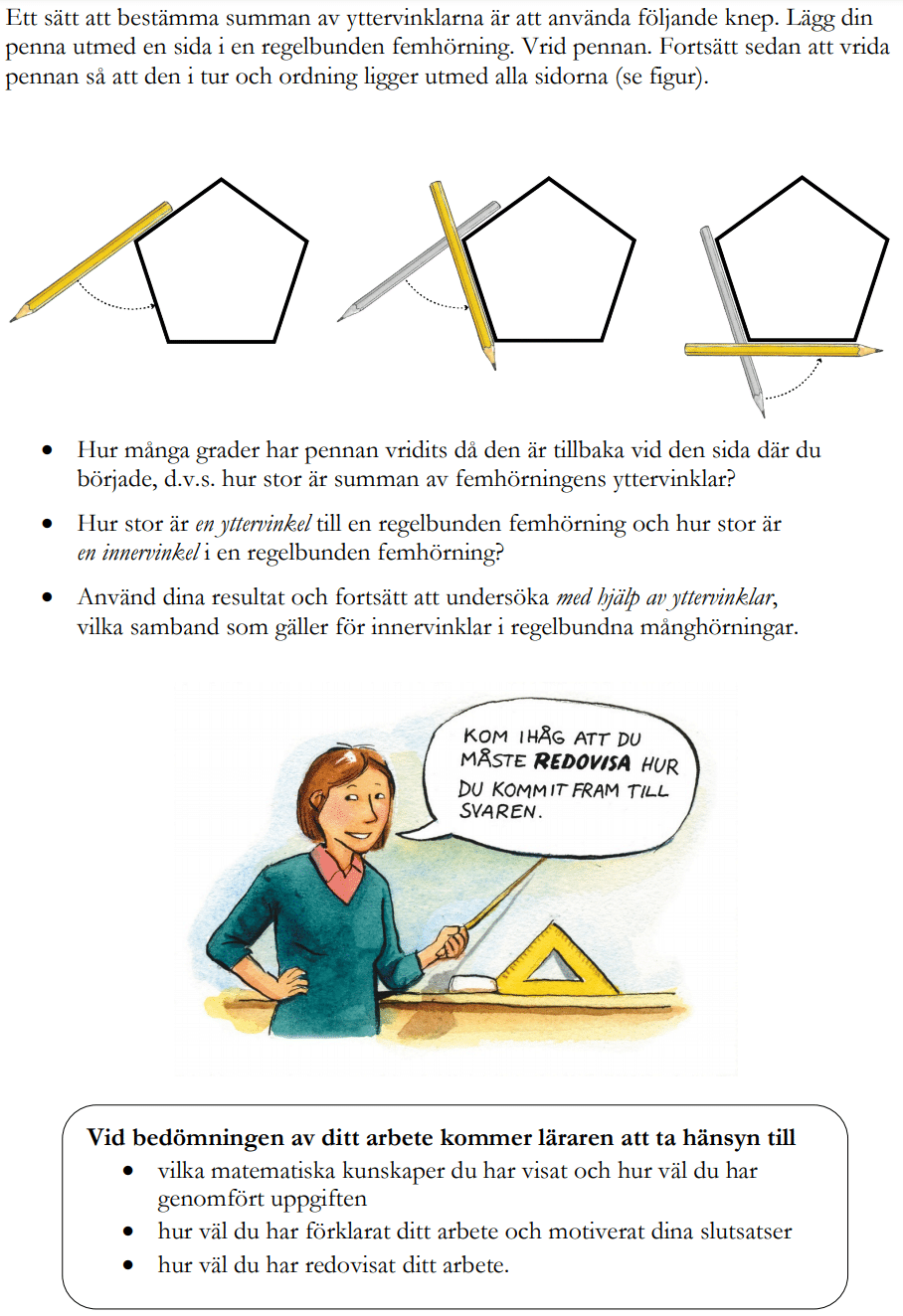
Från HT 2012, Vt 2014, HT 2014 och HT 2016 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 25).
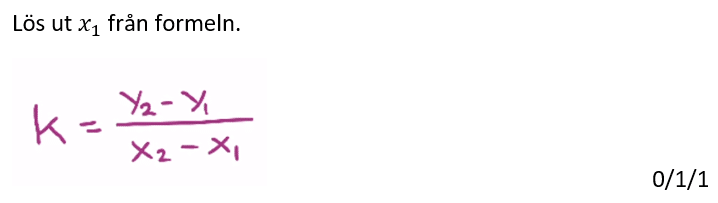
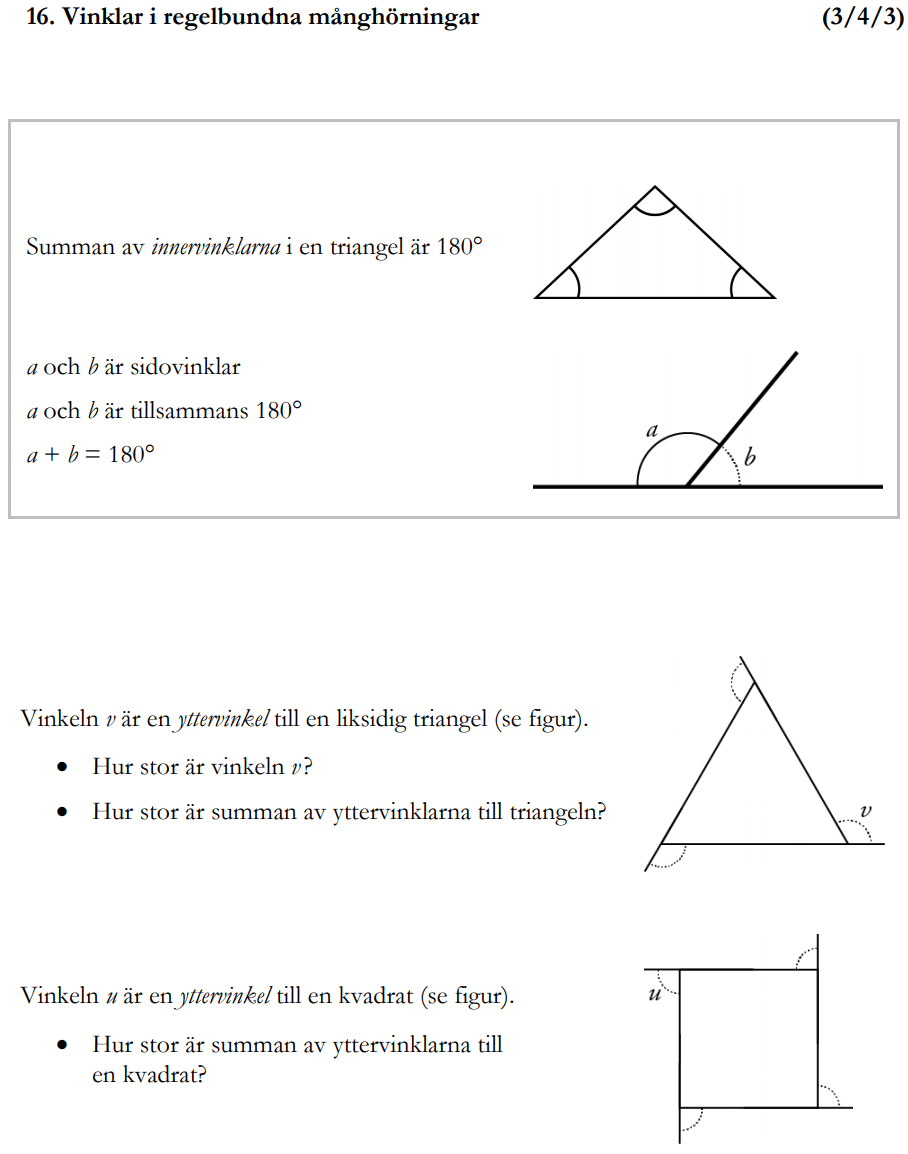
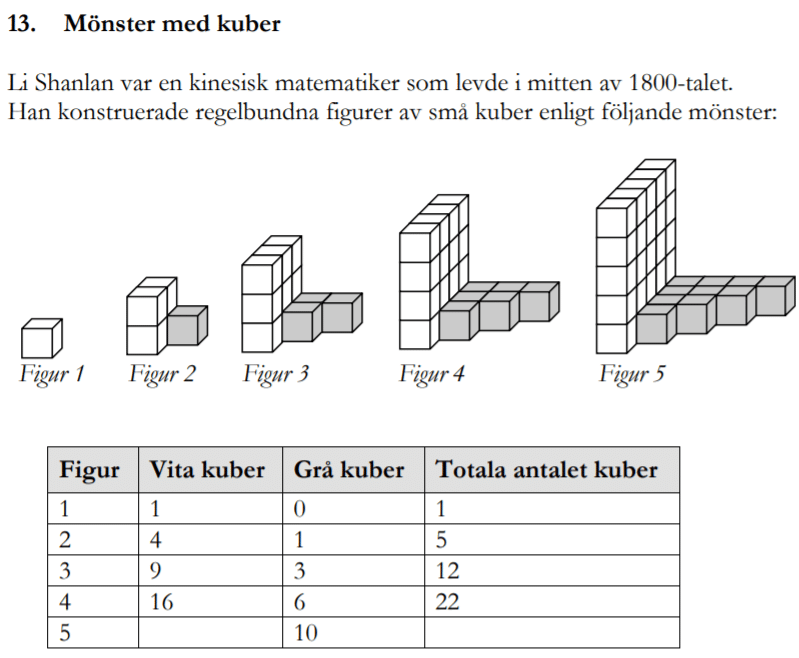
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b och 1c).
Bedömningsanvisningar/facit (uppgift 16).
På fråga 20 i kapitlet formler, måste man producera en formel som bevisar att A alltid är större, oavsett vilka värden på B man har? Jag satte direkt in 2 världen på B. Ett när B var vanligt och ett där B är dubbelt så stort och genom det kunde dra en slutsats att A blir större. Får man A poäng för det?
Uppskattar svar,
Hej! För full poäng räcker det inte att du endast provar två värden. Du måste också ha ett resonemang som förklarar varför det blir så, exempelvis att du beskriver att A blir större eftersom täljaren och nämnaren blir mer lika varandra, procentuellt sett. Täljaren blir en större andel av nämnaren och då närmar sig värdet på A mer och mer talet 1 ju större B blir. Då behövs ingen formel, men du måste förklara det med ord i så fall.
Mvh Jonas