Rationella uttryck: Introduktion och definitionsmängd 2

---

Sammanfattande bild:

Vad är ett rationellt uttryck?
För vilka värden är det inte definierat?

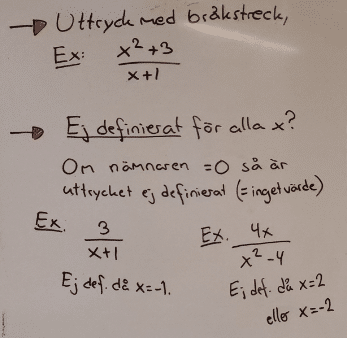
Vad är ett rationellt uttryck?
Finns det värden då uttrycket inte är definierat?

Liknande genomgång

Liknande genomgång

Uppgifter med videoförklaringar

Klicka på en uppgift för att se en videoförklaring

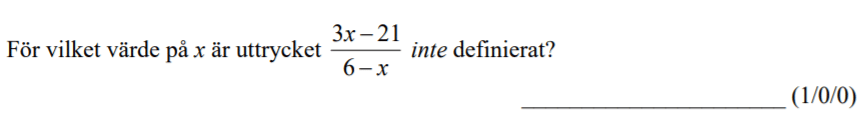
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.

Bedömningsanvisningar/facit (uppgift 2).

Från HT 2014 (Matematik 3b och 3c)

Bedömningsanvisningar/facit (uppgift 19).

Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 3b och 3c)

Bedömningsanvisningar/facit (uppgift 8).

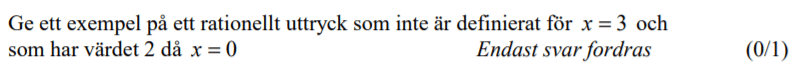
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.

Bedömningsanvisningar/facit (uppgift 11).

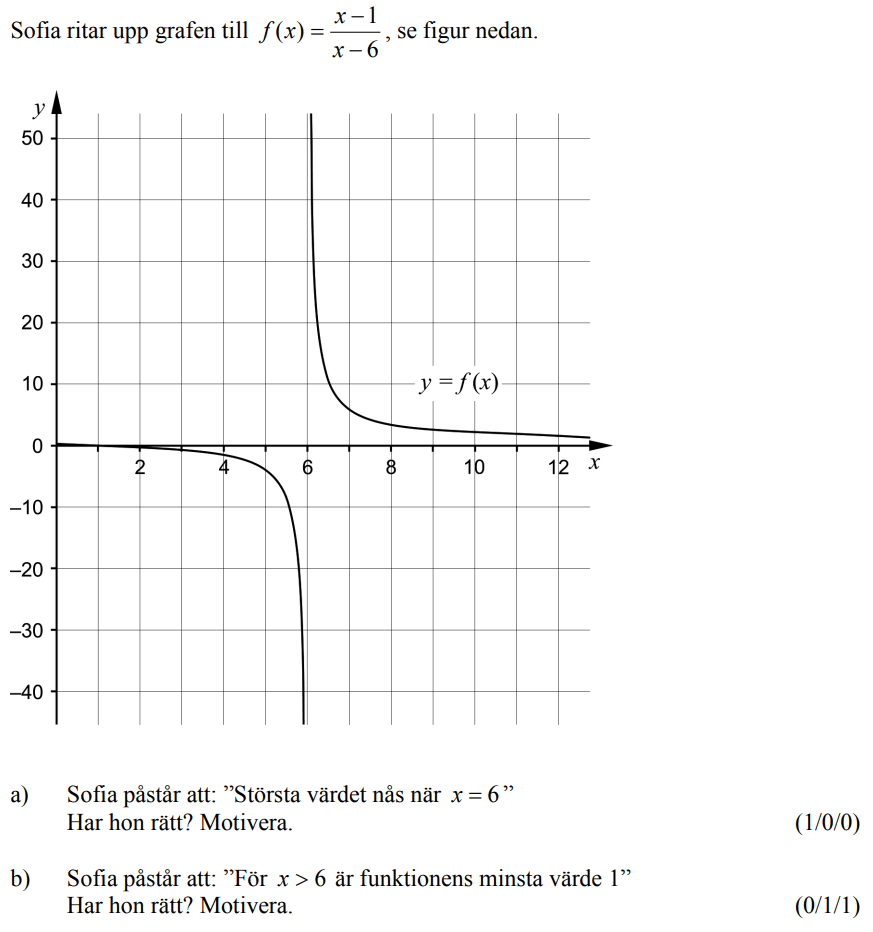
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)

Bedömningsanvisningar/facit (uppgift 9).

Löses utan digitala hjälpmedel. 
Från VT 2004 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).

Bedömningsanvisningar/facit (uppgift 8).
I filen ligger hela provhäftet med, så scrolla ner en bra bit.

---

---