Rötter, potensekvationer med heltalsexponenter samt upprepad procentuell förändring
Rötter och potensekvationer, samt uppgifter med exponentiell förändring
Liknande videor:
Del 1: Rötter och potensekvationer.
Kvadratrötter, Kubikrötter, andragradsekvationer, tredjegradsekvationer mm
Del 2: Upprepad procentuell förändring, y = Cax.
Potensekvationer dyker upp när förändringsfaktorn ska beräknas.
Ännu fler liknande genomgångar över samma innehåll
Rötter, potensekvationer och upprepad procentuell förändring.
Titta först på genomgångarna högst upp och försök sedan lösa uppgifterna i dessa genomgångar!
Fler uppgifter om exponentiell förändring
Rötter, andragradsekvationer och tredjegradsekvationer.
Rötter, potensekvationer och upprepad procentuell förändring.
Enkla andragradsekvationer och tredjegradsekvationer
Enkla andragradsekvationer och tredjegradsekvationer
Regler för rötter
Regler för rötter (t. ex. kvadratrötter)
Enklare grunder om rötter
Potensekvationer med rationella exponenter (bråk i exponenten)
Uppgifter från tidigare nationella prov:
Klicka på en uppgift för att se en videoförklaring
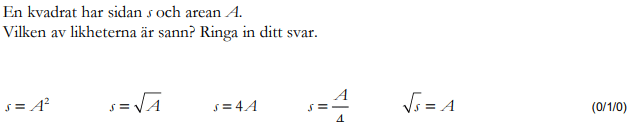
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 9).
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1c).
Bedömningsanvisningar/facit (uppgift 4).
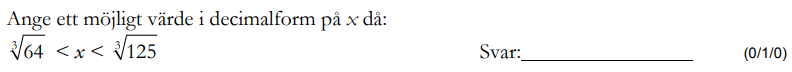
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 1c)
Bedömningsanvisningar/facit (uppgift 6).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 14).
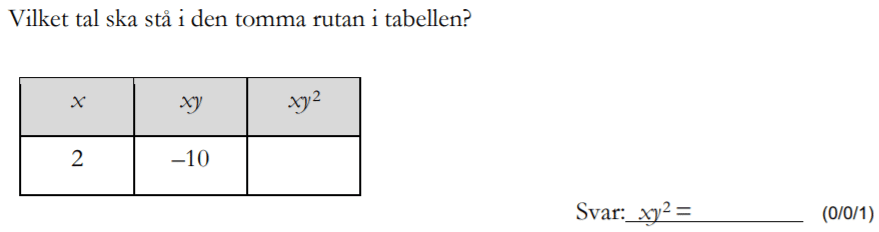
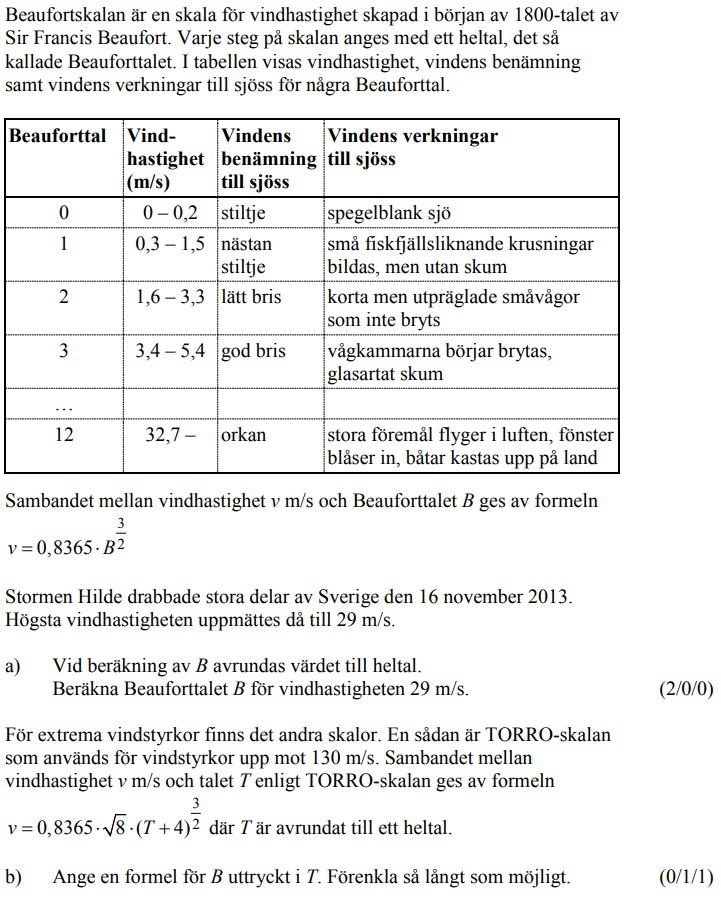
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 13).
Hej, jag har en fråga angående fjärdegradsekvation, d.v.s xˆ4. Om vi tar xˆ4 = -16. Då borde detta sakna reella lösning? I och med (-2)(-2)(-2)(-2) = 16. Rättar gärna mig om jag har fel.
Hej! Du har helt rätt! 🙂 Samma gäller för alla jämna exponenter, så om du har x^n=-16 så saknar den reell lösning om n är 2, 4, 6, 8, osv.
Mvh Jonas
Den sista uppgiften om xyˆ2 när vet man att xyˆ2 ska lika med (xy)°(xy)? Är det då det står (xy)ˆ2
Ja, då måste det vara en parentes utskriven. Annars gäller upphöjt alltid före multiplikation enligt prioriteringsreglerna (räkneordningen) vilket gör att exponenten bara gäller för det som står allra närmast.
Ett liknande exempel är -5^2 som inte har värdet 25, utan -25. Eftersom det innebär -5*5 och inte -5*(-5).
Däremot, om du skulle beräkna värdet av x^2 och får reda på att x=-5, då blir x^2=25. För när vi stoppar in värdet på x så måste vi använda parentes. x^2=(-5)(-5)=25.
Lycka till med matten 🙂 mvh Jonas
uppskattar att du har lagt ner all denna tid på att göra denna hemsida med genomgångar och bra uppgifter. kommer definitivt plugga mer med din hjälp till i Ma 2C! ToppenJobb
Stort tack! Bra idé, träning kommer helt klart ge färdighet! Kör hårt, men ha en skön sommar först! 🙂
(Fast nu kanske du redan är klar med 2c!)