Uppgifter i Matematik 3:
Rationella uttryck: Förenkla uttryck
Extra viktiga områden för E-nivå
Några områden är markerade med ”tumme upp” i menyn. Dessa områden måste du prioritera extra högt, speciellt om du kämpar för att klara kursen.
275 uppgifter med videoförklaringar, varav
170 från tidigare nationella prov.
Upplever du problem med att videor som du varit inne på tidigare inte startar vid rätt tidpunkt? Logga i så fall ut från ditt YouTubekonto och prova igen, alternativt öppna Vidma i inkognitoläge.
Nu kan du skriva ut uppgifterna [beta]
- Gå först in på det område du vill skriva ut.
- Välj sedan layout genom knapparna.
I utskriftsdialogrutan kan du ofta välja mellan att skriva ut till skrivare eller pdf-fil.
Andrés häften med uppgifter - att skriva ut
Min kollega André Nilsson har skapat jättebra häften med uppgifter från tidigare nationella prov. Dessa är perfekta att skriva ut och använda som träning för elever.
Observera att häftena är fristående från denna sida och att det finns uppgifter i häftena som inte finns på Vidma, men också tvärtom. Många av uppgifterna i häftet har alltså en videoförklaring, men de är sorterade på annat sätt på Vidma, så de kan vara svåra att hitta.
Till dig som får ha GeoGebra på nationella provet:
Här visar jag hur du löser att gäng uppgifter riktigt snabbt!
Uppgifter från nationella prov och från genomgångar.
Många av uppgifterna är från tidigare nationella prov, men det finns också ett antal uppgifter från mina egna genomgångar.
Uppgifterna från de nationella proven har tydliga bedömningsanvisningar, medan uppgifterna från mina egna genomgångar saknar detta än så länge. Dock finns videoförklaring till samtliga uppgifter där jag alltid berättar rätt svar.
Klicka på en uppgift för att se en videoförklaring till den!
Checklista E-nivå
Rationella uttryck
- Förståelse för vad ett rationellt uttryck är.
- Förstå för vilka värden ett uttryck är definierat och när det inte är det.
Matematik 5000 3b,
s. 25
1203
1204ab
1206
Origo 3b,
s. 30
1301
1302
1306
- Förkorta och förenkla ett rationellt uttryck, genom att först faktorisera täljare och nämnare.
Detta görs genom att först faktorisera täljare och nämnare (så att det vi vill förkorta sitter fast i övriga faktorer med multiplikation).
Faktorisering:
- Bryt ut gemensam faktor om sådan finns.
- Använd konjugatregeln eller kvadreringsreglerna baklänges.
- För högre betyg: Bryt ut (-1).
- För högre betyg: Faktorisera med hjälp av pq-formeln.
Matematik 5000 3b,
s. 29
1226
1227
1228
1229
1230
Origo 3b,
s. 30
1303
1304
1307
1308
- Addera, subtrahera, multiplicera och dividera rationella uttryck med varandra
Matematik 5000 3b,
s. 32, 34
1247
1250
1270
1271
1273
1275
1276
Origo 3b,
s. 33, 37
1311
1312
1313
1318
1319
1322
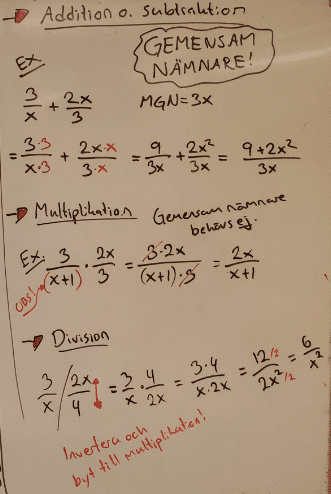
Addition och subtraktion:
Multiplikation och division:
- Lösa ekvationer där rationella uttryck ingår
Matematik 5000 3b,
s. 32, 34
1248
1249
1251
1257 a
Origo 3b,
s. 33, 37
1314
1320
1321
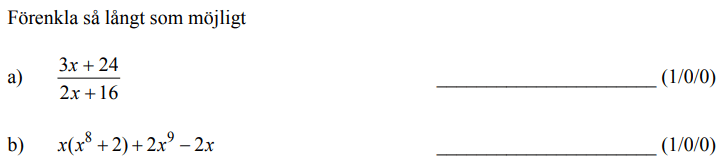
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 2).
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 5).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 14).
Löses utan digitala hjälpmedel.
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 6).
Löses utan digitala hjälpmedel.
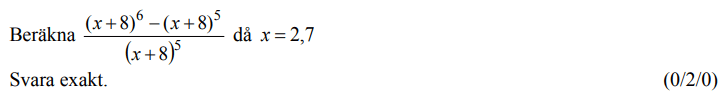
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 3b eller 3c)
Bedömningsanvisningar/facit (uppgift 14).