Uppgifter i Matematik 3:
Extremvärden och grafens utseende
Extra viktiga områden för E-nivå
Några områden är markerade med ”tumme upp” i menyn. Dessa områden måste du prioritera extra högt, speciellt om du kämpar för att klara kursen.
275 uppgifter med videoförklaringar, varav
170 från tidigare nationella prov.
Upplever du problem med att videor som du varit inne på tidigare inte startar vid rätt tidpunkt? Logga i så fall ut från ditt YouTubekonto och prova igen, alternativt öppna Vidma i inkognitoläge.
Nu kan du skriva ut uppgifterna [beta]

- Gå först in på det område du vill skriva ut.
- Välj sedan layout genom knapparna.
I utskriftsdialogrutan kan du ofta välja mellan att skriva ut till skrivare eller pdf-fil.
Andrés häften med uppgifter - att skriva ut
Min kollega André Nilsson har skapat jättebra häften med uppgifter från tidigare nationella prov. Dessa är perfekta att skriva ut och använda som träning för elever.
Observera att häftena är fristående från denna sida och att det finns uppgifter i häftena som inte finns på Vidma, men också tvärtom. Många av uppgifterna i häftet har alltså en videoförklaring, men de är sorterade på annat sätt på Vidma, så de kan vara svåra att hitta.
Till dig som får ha GeoGebra på nationella provet:
Här visar jag hur du löser att gäng uppgifter riktigt snabbt!
Uppgifter från nationella prov och från genomgångar.
Många av uppgifterna är från tidigare nationella prov, men det finns också ett antal uppgifter från mina egna genomgångar.
Uppgifterna från de nationella proven har tydliga bedömningsanvisningar, medan uppgifterna från mina egna genomgångar saknar detta än så länge. Dock finns videoförklaring till samtliga uppgifter där jag alltid berättar rätt svar.
Klicka på en uppgift för att se en videoförklaring till den!
- Dölj checklista
- Visa checklista mm.
Checklista E-nivå
Undersöka grafens utseende och extrempunkter med hjälp av derivata
- Kunna avläsa på en graf inom vilka intervall som en funktion är växande, avtagande eller har derivatan 0.
- Förståelse för begreppet extrempunkt, vilket är ett samlingsnamn för minimipunkt, maximipunkt, terrasspunkt.
- Förståelse för att extrempunkter hittas där derivatan är 0, alltså derivatans nollställe.
- Kunna beräkna extrempunkternas koordinater, även y-värdet.
- Kunna använda teckentabell för att visa grafens utseende och avgöra extrempunkternas karaktär.
- Kunna göra en tydlig skiss av grafen, med extrempunkterna tydligt utsatta.
Matematik 5000 3b,
s. 136
3108
3109
3110
3111
3112
3113
3114
s. 141
3117
3118
3119
3120
3121
Origo 3b,
s. 138-139
4101
4102
4103
s. 143
4111
4112
4113
s. 147
4201
4202
4203
4204
4205
4206
Introduktion: Viktiga begrepp
- Extrempunkter (lokala och globala).
- Extremvärden.
- Terrasspunkter.
- Teckentabell.
- Avtagande intervall.
- Växande intervall.
- Ändpunkter i intervallet är också extrempunkter.
Hitta extrempunkterna, avgöra karaktären med hjälp av teckentabell eller andraderivata, samt skissa grafen.
Tre exempeluppgifter:
Att ta reda på största och minsta värdet, i ett intervall
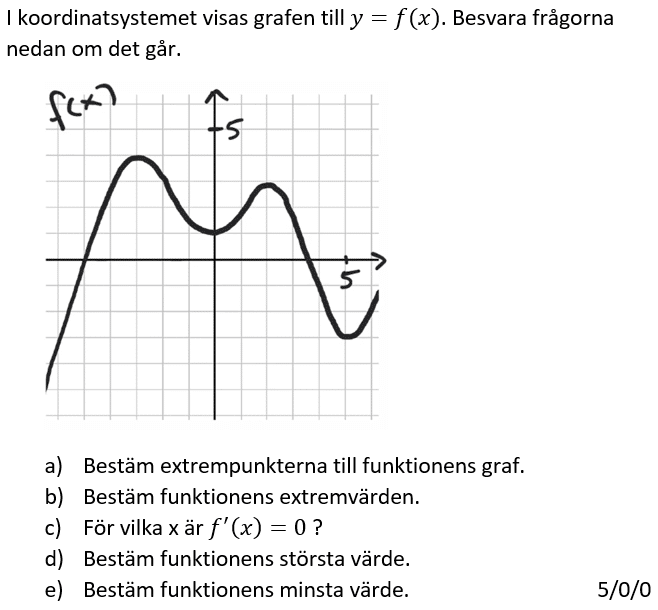
Löses utan digitala hjälpmedel.
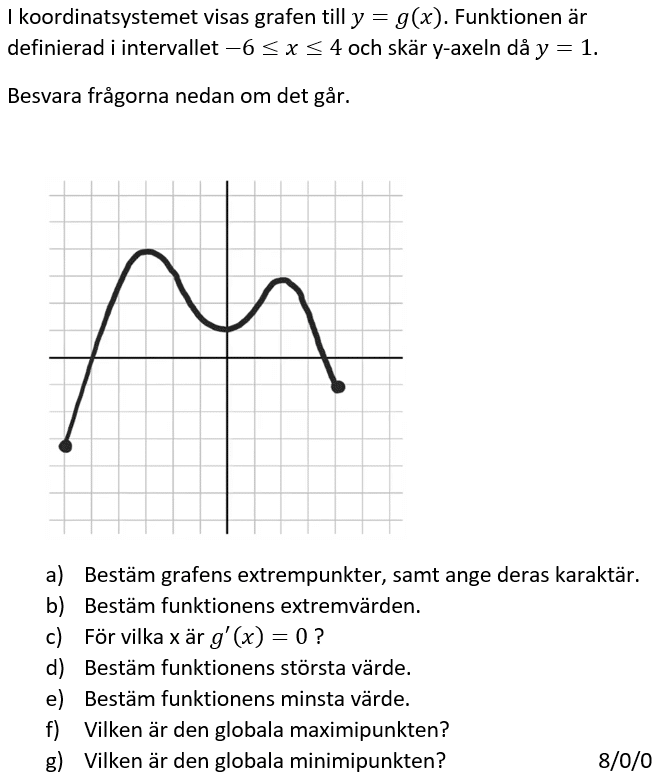
Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 3b och 3c)
Bedömningsanvisningar/facit (uppgift 13).

Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 3b eller 3c).
Videoförklaringen är gjord av min tidigare kollega David Johansson.

I videoförklaringen formuleras frågan inte på riktigt samma sätt, men skillnaderna och likheterna bör bli tydliga om du tittar på de inledande minutrarna.
Löses utan digitala hjälpmedel.
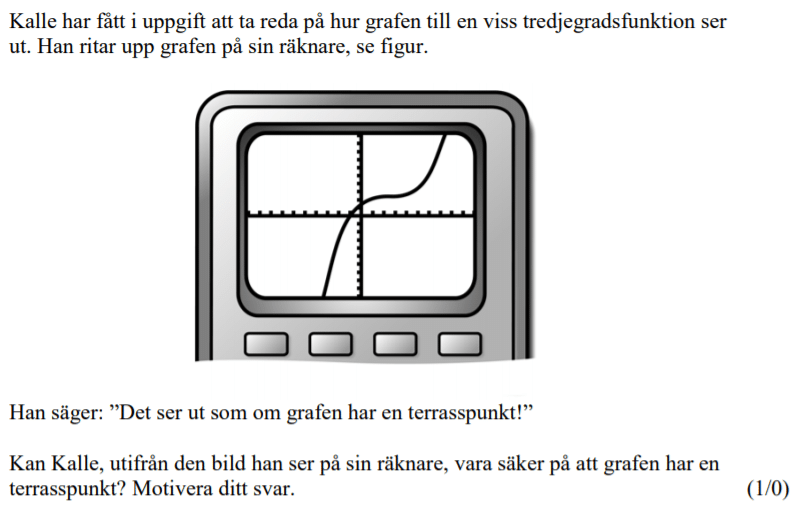
Löses utan digitala hjälpmedel.
Från VT 2011 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Videoförklaringen är gjord av min tidigare kollega David Johansson.
Bedömningsanvisningar/facit (uppgift 3).

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.
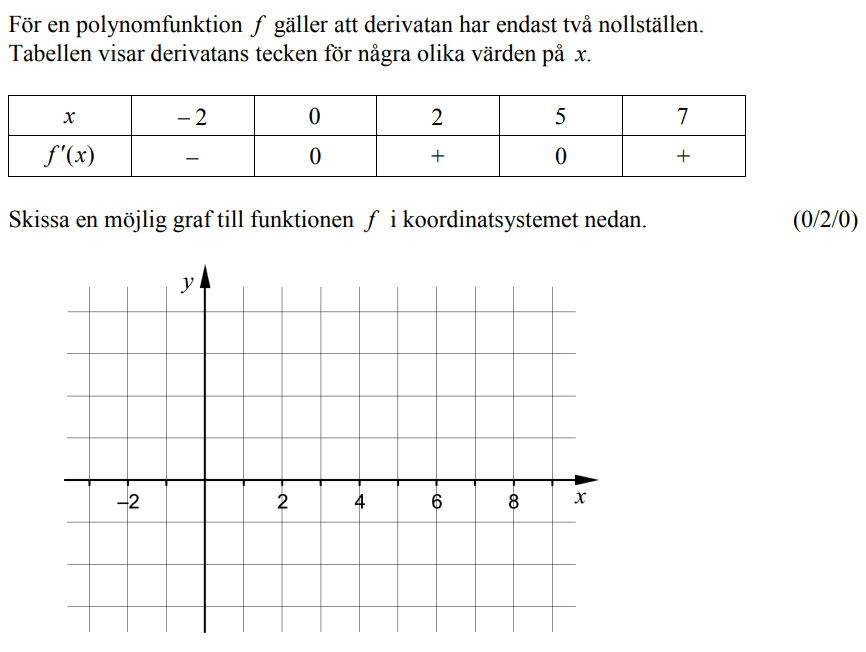
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 3b och 3c)
Bedömningsanvisningar/facit (uppgift 7).
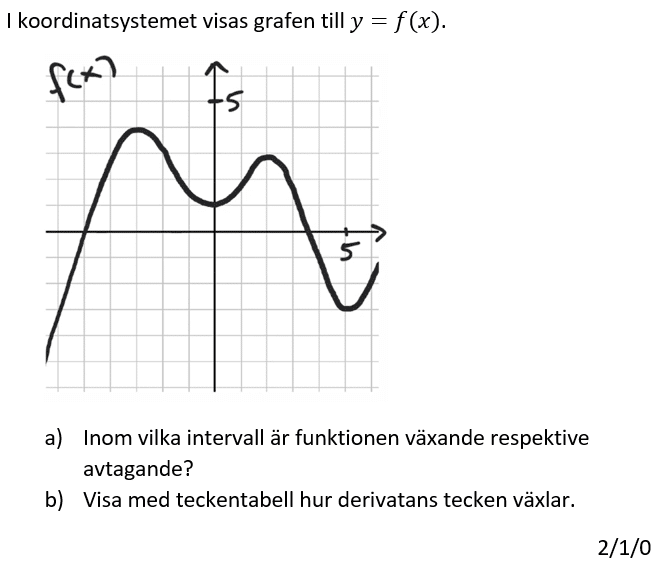
Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Från VT 2012 (Tidigare kursen Matematik C, vilket gör att poängmarkeringen ser annorlunda ut).
Bedömningsanvisningar/facit (uppgift 15).
I filen ligger hela provhäftet med, så scrolla ner en bra bit.

Löses utan digitala hjälpmedel.



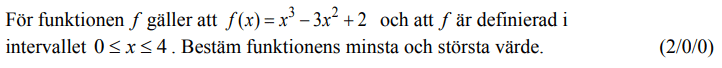

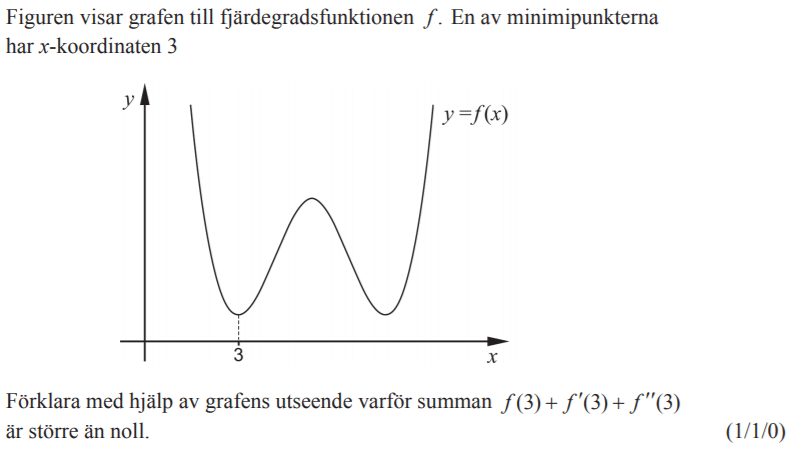
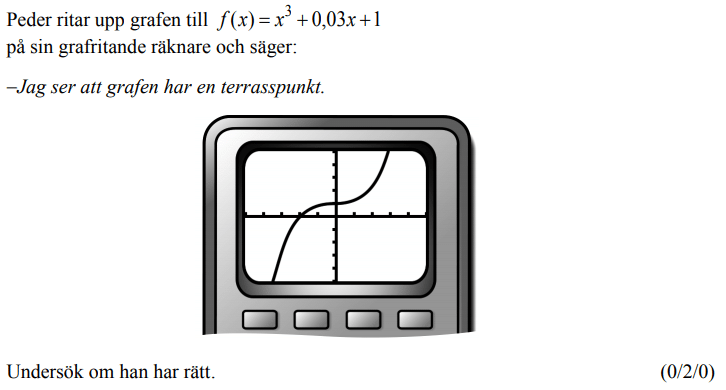
facit länken på uppgift 5 i extremvärden och grafens utseende är felaktig eller så är fel uppgift angiven