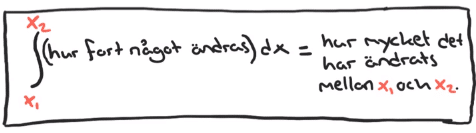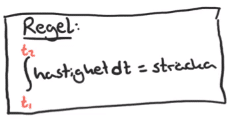Dagsarkiv: 2 april, 2019

Det viktigaste i Matematik 3b 42

Det allra viktigaste i Matematik 3b

Checklista, genomgångar och de drygt 100 viktigaste uppgifterna ifrån boken.

Detta är en översikt över det allra viktigaste innehållet i kursen Matematik 3b, samt förslag på uppgifter du bör prioritera om du har hamnat efter i kursen eller behöver repetera inför nationella provet.

Fokus här är uppgifter på E-nivå. 

Observera: Detta är inte allt kursinnehåll utan endast det som jag bedömer är viktigast att träna på för att lyckas på Nationella provet.

JÄTTEBRA TIPS:

Använd Fredriks Filmer tillsammans med denna sida i varsin flik. Där finns videoförklaringar till nästan alla uppgifter från Matematik 5000-boken. Då kan du direkt se en förklaring på uppgifter du inte kan. 

Denna sida tillhör ej vidma, utan det är läraren Fredrik Lindmark som gjort ett stort jobb med att spela in uppgiftslösningar.

Till videoförklaringarna

Rationella uttryck

  • Förståelse för vad ett rationellt uttryck är.
  • Förstå för vilka värden ett uttryck är definierat och när det inte är det.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 25

1203

1204ab

1206  

Origo 3b,
s. 30

1301

1302

1306

  • Förkorta och förenkla ett rationellt uttryck, genom att först faktorisera täljare och nämnare.

Detta görs genom att först faktorisera täljare och nämnare (så att det vi vill förkorta sitter fast i övriga faktorer med multiplikation).

Faktorisering:

  1. Bryt ut gemensam faktor om sådan finns.
  2. Använd konjugatregeln eller kvadreringsreglerna baklänges.
  3. För högre betyg: Bryt ut (-1).
  4. För högre betyg: Faktorisera med hjälp av pq-formeln.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 29

1226

1227

1228

1229

1230

 

Origo 3b,
s. 30

1303

1304

1307

1308

 

  • Addera, subtrahera, multiplicera och dividera rationella uttryck med varandra

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b,
s. 32, 34

1247

1250

1270

1271

1273

1275

1276

Origo 3b,
s. 33, 37

1311

1312

1313

1318

1319

1322

 

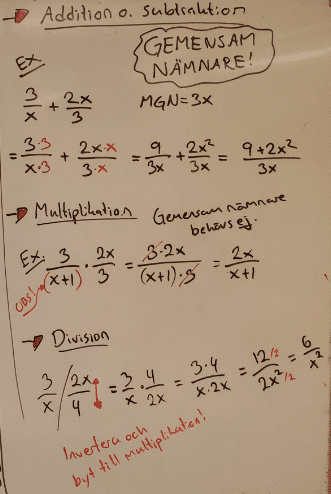
Addition och subtraktion:
Multiplikation och division:
  • Lösa ekvationer där rationella uttryck ingår

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 32, 34

1248

1249

1251

1257 a

Origo 3b,
s. 33, 37 

 

1314

1320

1321

 

Fler genomgångar om rationella uttryck

Ändringskvot: Δy / Δx

  • Förståelse för begreppen ändringskvot (differenskvot), sekant, genomsnittlig förändringshastighet.
  • Kunna beräkna ändringskvoten utifrån en graf, men också i verklighetsbaserade exempel.
  • Kunna tolka innebörden av ändringskvot i verklighetsbaserade exempel.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 75

2104

2105

2106

2107

2108

2109 

2112

2114

Origo 3b,
s. 75

2201

2203

2204

2205

2207

2208

Innebörden av derivata och skrivsättet f'(x)

  • Förståelse för skillnaden mellan sekant och tangent, samt skillnaden mellan genomsnittlig förändringshastighet (ändringskvot) och derivata.
  • Kunna avgöra var på en kurva som tangentens lutning (derivatan) har positivt värde, negativt värde eller värdet 0.
  • Kunna tolka innebörden av derivata i verklighetsbaserade exempel.
  • Förståelse för skrivsättet f'(x).

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 81-82

2124

2125

2126

2127

2128

2129

2131

2132

2133

2134

2137

 

Origo 3b,
s. 79-80

2213

2214

2215

2216

2218

2219

s. 88-89

2317

2318

2319

2320

2322

2324

 

Deriveringsregler

  • Kunna derivera polynomfunktioner

Med detta menas funktioner som kan innehålla konstanttermer, x-termer, x2-termer, x3-termer, etc.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 92

2305

2306

2307

2308

2309

2312 (Kom ihåg innebörden)

2313 (Kom ihåg innebörden)

2314

2318

Origo 3b,
s. 105, 107

3101

3102

3103

3104

3105

3106

3108

3114

3115

3116

3117

3118

3119

3120

3121

 

 

Formler:

Klicka för förstoring.
Klicka för förstoring.
  • Kunna derivera exponentialfunktioner med basen e

Med detta menas funktioner med någon potens, där e är potensens bas och x finns i exponenten.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 104

2405

2406

2407

2408

2410

2411

2430 (Kom ihåg innebörden)

Origo 3b,
s. 114-115, 118

3201

3202

3203

3204

3205

3207

3208

3217 a, c

3218 a, c, d

 

Formler:

Fokusera på de två nedersta formlerna.

Klicka för förstoring.

Tillämpningar av derivata

  • Förståelse för hur du kan lösa verklighetsbaserade problem med hjälp av derivata.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 92-93

2312

2313

2324

 

s. 111

2454

2455

2458

2459

2460

 

 

Origo 3b,
s. 122

3230

3231

3232

3234

3235

3237

3238

 

Undersöka grafens utseende och extrempunkter med hjälp av derivata

  • Kunna avläsa på en graf inom vilka intervall som en funktion är växande, avtagande eller har derivatan 0.
  • Förståelse för begreppet extrempunkt, vilket är ett samlingsnamn för minimipunkt, maximipunkt, terrasspunkt.
  • Förståelse för att extrempunkter hittas där derivatan är 0, alltså derivatans nollställe.
  • Kunna beräkna extrempunkternas koordinater, även y-värdet.
  • Kunna använda teckentabell för att visa grafens utseende och avgöra extrempunkternas karaktär.
  • Kunna göra en tydlig skiss av grafen, med extrempunkterna tydligt utsatta.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 136

3108

3109

3110

3111

3112

3113

3114

 

s. 141

3117

3118

3119

3120

3121

 

Origo 3b,
s. 138-139

4101

4102

4103

 

s. 143

4111

4112

4113

 

s. 147

4201

4202

4203

4204

4205

4206

 

Introduktion: Viktiga begrepp

  • Extrempunkter (lokala och globala).
  • Extremvärden.
  • Terrasspunkter. 
  • Teckentabell.
  • Avtagande intervall. 
  • Växande intervall. 
  • Ändpunkter i intervallet är också extrempunkter.

Hitta extrempunkterna, avgöra karaktären med hjälp av teckentabell eller andraderivata, samt skissa grafen.

Tre exempeluppgifter:

Att ta reda på största och minsta värdet, i ett intervall

Fler genomgångar om detta

Tillämpningar: extremvärdesproblem

  • Förståelse för hur du med hjälp av derivata kan lösa verklighetsbaserade problem där det gäller att hitta största eller minsta värdet för någonting.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 147-148

3202

3203

3205

3206

3207

3210

 

Origo 3b,
s. 157

4243

4244

4245

 

s. 163-164

13

16

 

Fler genomgångar om detta

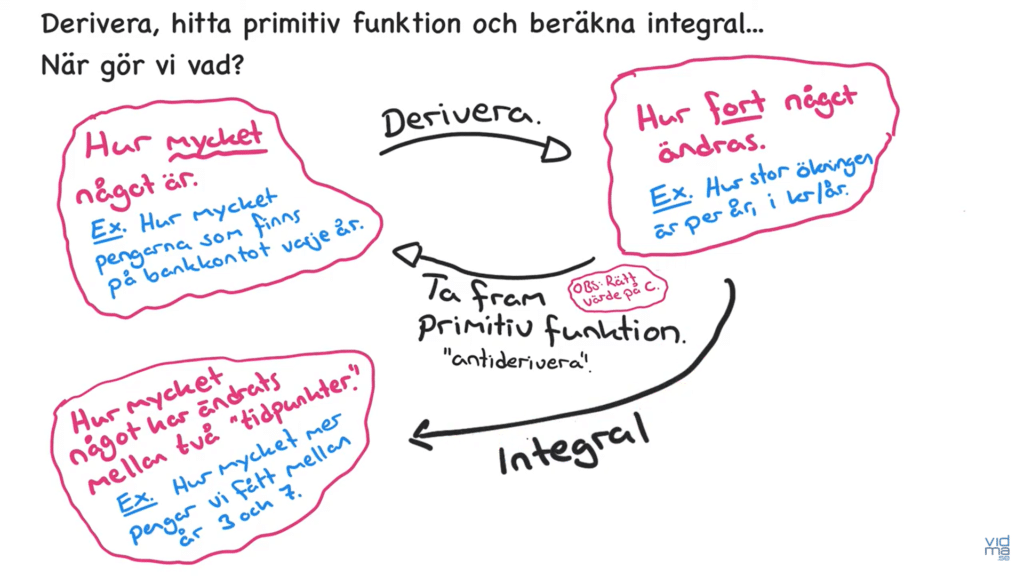
Primitiva funktioner och integraler

  • Kunna ta fram en, eller samtliga primitiva funktioner till en given polynomfunktion.
  • Förstå skrivsättet F(x) och att det är den primitiva funktionen till f(x).

Med polynomfunktion menas funktioner som kan innehålla konstanttermer, x-termer, x2-termer, x3-termer, etc.

  • Kunna ta fram en, eller samtliga primitiva funktioner till en given exponentialfunktion med talet e som bas..

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 171

3303

3304

3305

3306

3307

3308

3309

3310

 

Origo 3b,
s. 172

5101

5102

5103

5108

 

Fler genomgångar om detta
  • Kunna ta fram en specifik primitiv funktion, som uppfylls av ett givet villkor.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 173

3317

3318

3319

 

Origo 3b,
s. 177

5128

5129

5130

 

Fler genomgångar om detta
  • Förstå innebörden av en integral, skrivsättet och att integralen motsvarar en area under en graf.
  • Förstå begreppen undre och övre integrationsgräns, samt integrationsvariabel.
  • Kunna uppskatta värdet av en integral genom att titta på grafen och "räkna rutor" (grovt uppskatta arean).

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 176

3402

3403

3404

3406

 

Origo 3b,
s. 182

5201

5202

5203

5204

 

Fler genomgångar om detta
  • Förstå skrivsättet för att beräkna en integral.
  • Kunna beräkna integraler över samma typ av funktioner som du kan göra primitiv funktion för.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 181

3412

3413

3415

3416

3417

 

Origo 3b,
s. 187

5211

5212

5213

5214

5215

 

Klicka för förstoring
Fler genomgångar om detta

Tillämpningar: integraler

  • Förståelse för hur du med hjälp av integraler kan lösa verklighetsbaserade problem.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 184

3421

3422

3423

3424

3426

 

Origo 3b,
s. 195

5318

5319

5320

5321

5324

 

Videoförklaring till bilden ovan! Klippet startar på rätt ställe.

Fler genomgångar om detta

Geometrisk summa

  • Förståelse för hur en geometrisk talföljd och summa är uppbyggd och hur du beräknar en geometrisk summa.
  • Kunna lösa tillämpningsuppgifter som innehåller procentuell tillväxt, med hjälp av geometrisk summa.

OBS: Uppgifterna nedan är från de GAMLA böckerna, som trycktes innan 2021.

Matematik 5000 3b, 
s. 203

4103

4104

4105

4106

4115

4116

4117

4119

 

Origo 3b,
s. 218-219

6201

6202

6204

6205

6208

6209