Uppgifter i Matematik 4:
Deriveringsregler
Notera att proven från VT 2015 och VT 2016 inte är inlagda här. Videoförklaringar till dessa finns dock här: https://vidma.se/np4.
Hela nationella prov
Ännu fler genomräknade uppgifter än de som finns ovan! Här finns även VT 2015 och VT 2015.
Blandade uppgifter
Utvalda blandade uppgifter
– perfekta att också skriva ut som häften.
194 uppgifter med videoförklaringar, varav
141 från tidigare nationella prov.
Upplever du problem med att videor som du varit inne på tidigare inte startar vid rätt tidpunkt? Logga i så fall ut från ditt YouTubekonto och prova igen, alternativt öppna Vidma i inkognitoläge.
Nu kan du skriva ut uppgifterna [beta]

- Gå först in på det område du vill skriva ut.
- Välj sedan layout genom knapparna.
I utskriftsdialogrutan kan du ofta välja mellan att skriva ut till skrivare eller pdf-fil.
Uppgifter från nationella prov och från genomgångar.
Många av uppgifterna är från tidigare nationella prov, men det finns också ett antal uppgifter från mina egna genomgångar.
Uppgifterna från de nationella proven har tydliga bedömningsanvisningar, medan uppgifterna från mina egna genomgångar saknar detta än så länge. Dock finns videoförklaring till samtliga uppgifter där jag alltid berättar rätt svar.
Klicka på en uppgift för att se en videoförklaring till den!
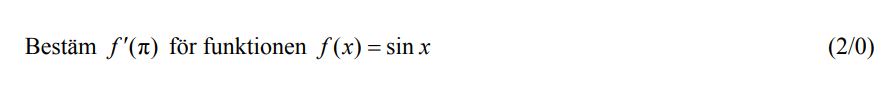
Löses utan digitala hjälpmedel. Från VT 2012 (Matematik D).
Bedömningsanvisningar/facit (uppgift 1).

Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 2).
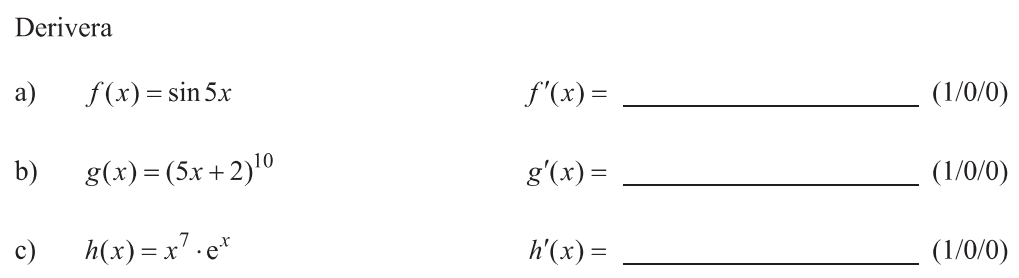
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 1).

Löses utan digitala hjälpmedel. Från VT 2013 (Matematik D).
Bedömningsanvisningar/facit (uppgift 2).

Löses utan digitala hjälpmedel. Från VT 2012 (Matematik D).
Bedömningsanvisningar/facit (uppgift 2).

Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 1).
(Uppgiften har inget med deriveringsregler att göra, men den skulle känna sig ensam om den skulle behöva ligga helt själv på en egen sida).
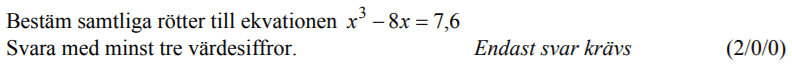
Från VT 2014 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 25).
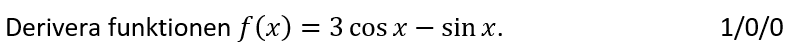
Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 1).

Löses utan digitala hjälpmedel. Från VT 2011 (Matematik D).
Bedömningsanvisningar/facit (uppgift 2).
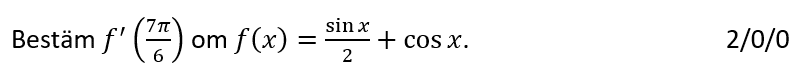
Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.

Löses utan digitala hjälpmedel.
Kommentar: Jag slarvar lite med funktionsbeteckningarna när jag skriver den inre funktion och den yttre funktionen, samt deras derivator. Korrekt är att använda beteckningarna y(u), y'(u), u(x) och u'(x). Notera att beteckningen y'(x) endast får användas för det sista funktionsuttrycket, när vi multiplicerar ihop den inre och den yttre derivatan. Se mer här om detta: https://youtu.be/_WNGpaR0kRg.
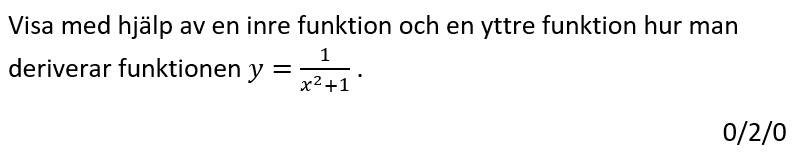
Löses utan digitala hjälpmedel.
Kommentar: Jag slarvar lite med funktionsbeteckningarna när jag skriver den inre funktion och den yttre funktionen, samt deras derivator. Korrekt är att använda beteckningarna y(u), y'(u), u(x) och u'(x). Notera att beteckningen y'(x) endast får användas för det sista funktionsuttrycket, när vi multiplicerar ihop den inre och den yttre derivatan. Se mer här om detta: https://youtu.be/_WNGpaR0kRg.
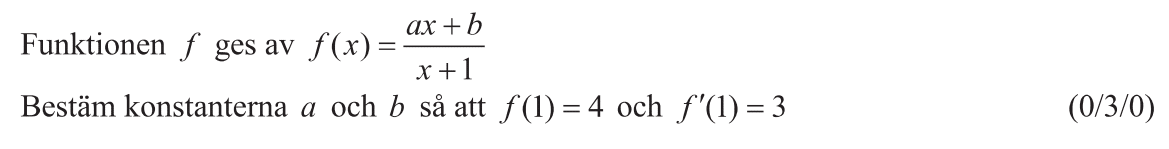
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 17).

Löses utan digitala hjälpmedel.
Kommentar: Jag slarvar lite med funktionsbeteckningarna när jag skriver den inre funktion och den yttre funktionen, samt deras derivator. Korrekt är att använda beteckningarna y(u), y'(u), u(x) och u'(x). Notera att beteckningen y'(x) endast får användas för det sista funktionsuttrycket, när vi multiplicerar ihop den inre och den yttre derivatan. Se mer här om detta: https://youtu.be/_WNGpaR0kRg.
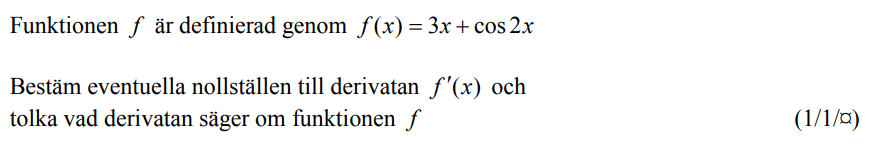
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik D).
Bedömningsanvisningar/facit (uppgift 18).
Kommentar: a-uppgiften är om derivata och passar därför i den här fliken.

Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 18).
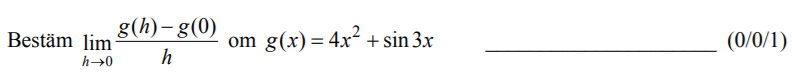
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 10).
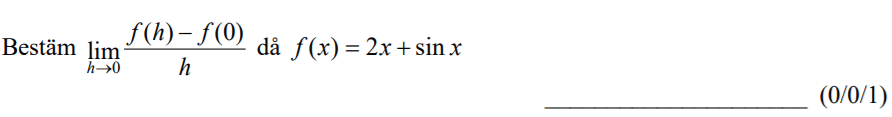
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 7).
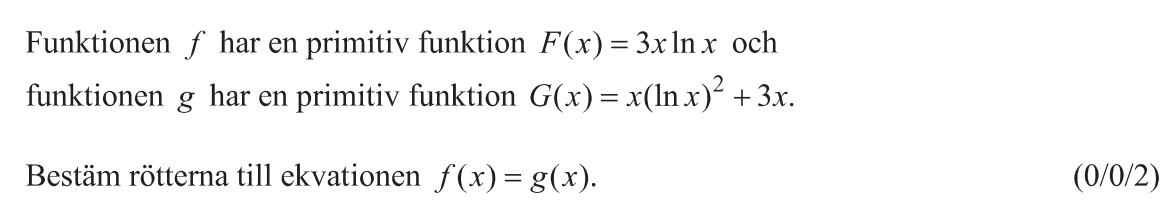
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 19).

Löses utan digitala hjälpmedel.
Kommentar: Jag slarvar lite med funktionsbeteckningarna när jag skriver den inre funktion och den yttre funktionen, samt deras derivator. Korrekt är att använda beteckningarna y(u), y'(u), u(x) och u'(x). Notera att beteckningen y'(x) endast får användas för det sista funktionsuttrycket, när vi multiplicerar ihop den inre och den yttre derivatan. Se mer här om detta: https://youtu.be/_WNGpaR0kRg.


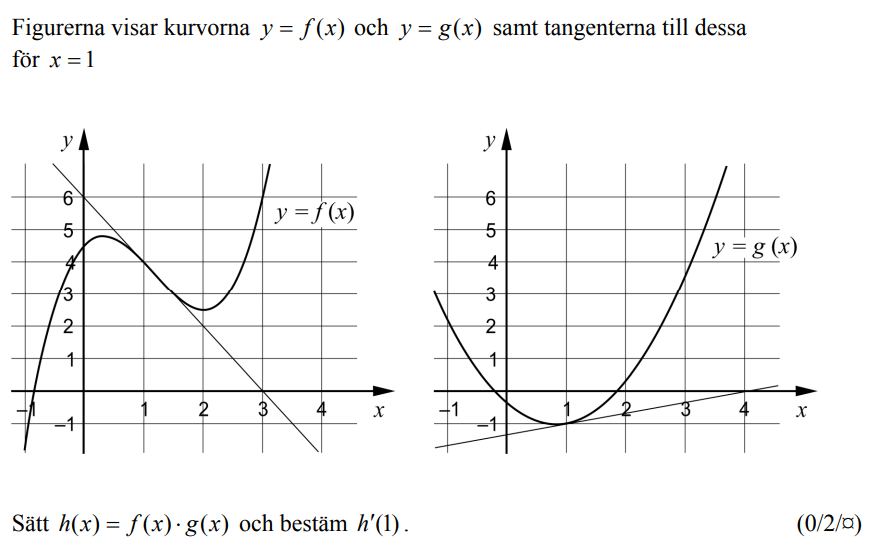
Hej Jonas, Vet inte om du vet om det men jag märkte att uppgift 17 skiljer från förklarings videon lite grann. nämnaren i videon har termen 2x^4 medans i uppgiften är det 2x^2. Vart lite förvirrad en stund innan jag visste att det inte var samma fråga.