Under konstruktion - allt är inte klart.
Klara Matte 2
- en sida för dig som tänker nå ett E.
Välj kurs:
Matematik 2b och 2c
Hej! Läs detta först.
Hej! Denna sida är tänkt att vara en hjälp för dig som kämpar för att klara Matematik 2. Det här är ett komplement till den vanliga undervisning och ditt ordinarie läromedel.
- Kanske har du hamnat efter i kursen och behöver göra en omstart?
- Kanske behöver du titta på de viktigaste genomgångarna igen?
- Kanske vill du träna på utvalda uppgifter (där många är från nationella prov) och kunna se videoförklaringar till dem?
Din plan:
- Titta på genomgångarna.
- Arbeta med uppgifterna här på sidan.
- Titta på videoförklaringarna när du kör fast. Se till att verkligen försöka förstå. Skriv upp viktiga saker och exempel i ett särskilt häfte.
- Gå tillbaka och gör de knepiga uppgifterna igen efter några dagar.
- Repetera regelbundet sådant som du gjort tidigare.
- Bestäm dig. Och tro på dig själv!
1. Grunder i algebra (från Matematik 1)
1.1 Uttryck och ekvationer
Detta är viktiga grunder som du måste behärska. I jättemånga uppgifter i Matematik 2 krävs att du kan förenkla uttryck och lösa ekvationer, även om just detta inte testas specifikt.
Checklista
- Förenkla uttryck
- Med parenteser
- Med nämnare
- Lösa ekvationer
- Med parenteser
- Med nämnare
- Beräkna värdet av ett uttryck om du får veta variablernas värde
- Ställa upp ett uttryck för att kunna lösa ett problem
Viktigaste genomgångarna
Förenkla enkla uttryck
Förenkla uttryck med parenteser
Lösa enkla ekvationer
Något svårare ekvationer
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1c).
Bedömningsanvisningar/facit (uppgift 1).
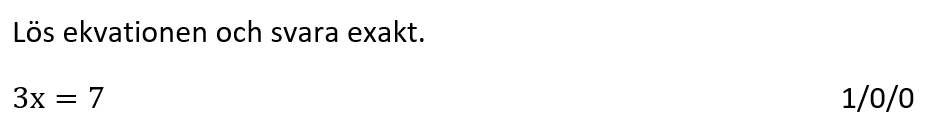
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a).
Bedömningsanvisningar/facit (uppgift 8).
Löses utan digitala hjälpmedel. Från egen genomgång.
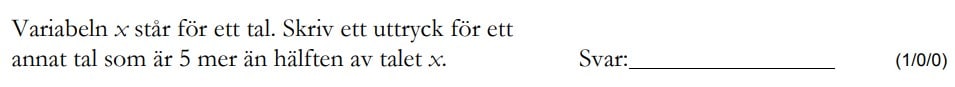
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 1b).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 3).
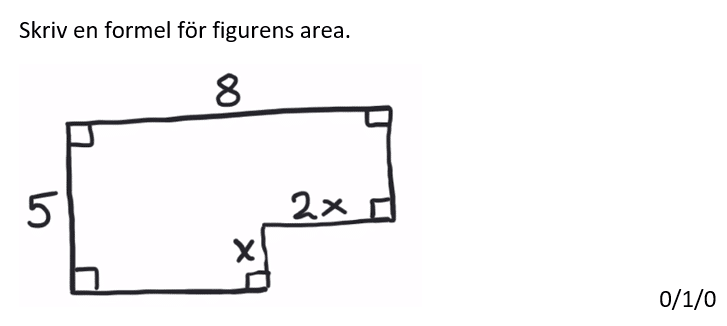
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 2).
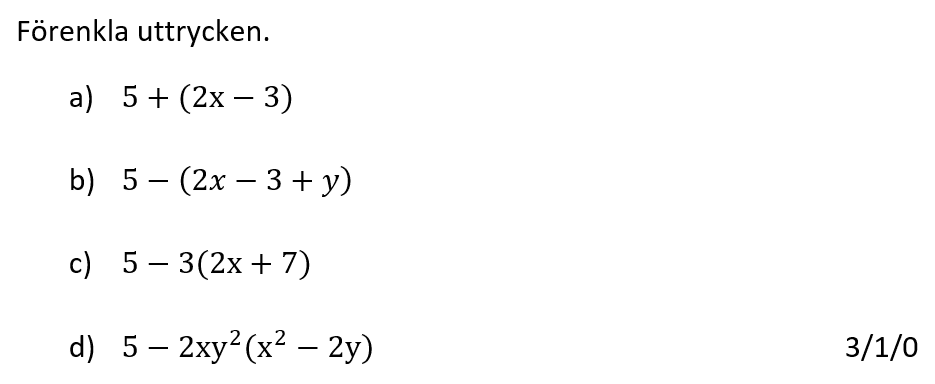
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 6).
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 9).
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 1b).
Bedömningsanvisningar/facit (uppgift 5).
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 12).
Fler uppgifter finns här:
2. Grunder om funktioner och linjära samband (Från Matematik 1)
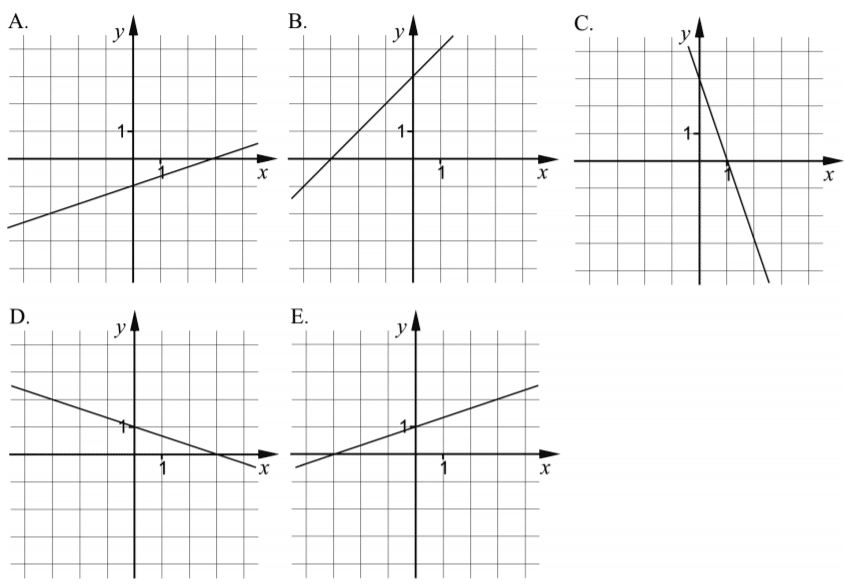
2.1 Räta linjens ekvation
Checklista
- Räta linjens ekvation (repetition, men grunderna behövs)
- Rita grafen
- Läsa av ekvationen för en linje
- Beräkna linjens lutning om du får veta två punkter som linjen går igenom.
Viktigaste genomgångarna
Förstå räta linjens ekvation
Förstå räta linjens ekvation
Uppgift 2 är för högre betyg.
Exempeluppgift om parallella linjer
Parallella och vinkelräta linjer, samt olika former för räta linjens ekvation
Uppgifter med videoförklaringar
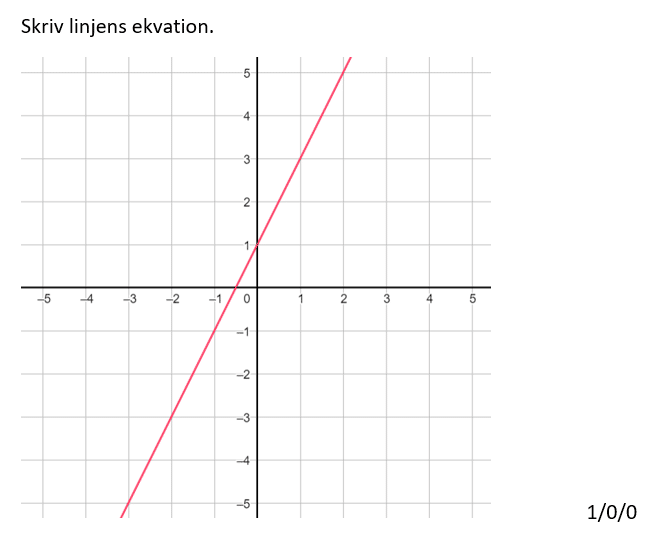
Löses utan digitala hjälpmedel.
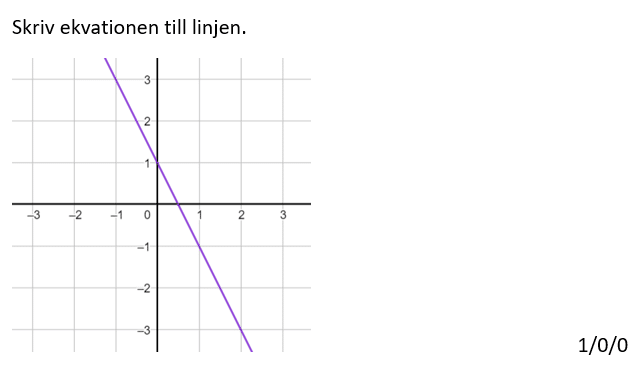
Löses utan digitala hjälpmedel.
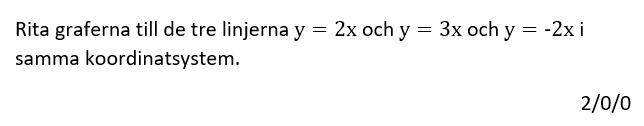
Löses utan digitala hjälpmedel.
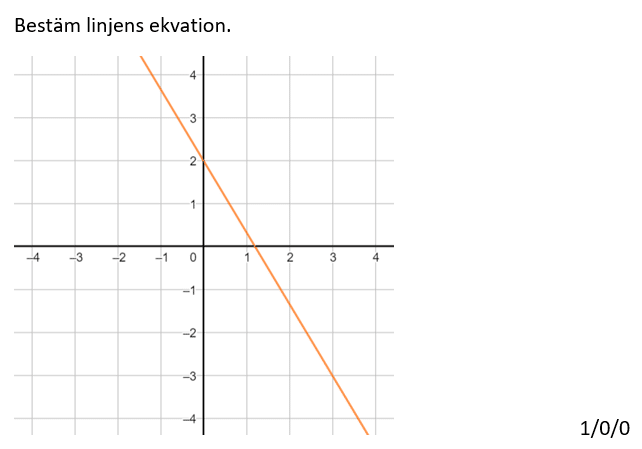
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a).
Bedömningsanvisningar/facit (uppgift 1).
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 1).
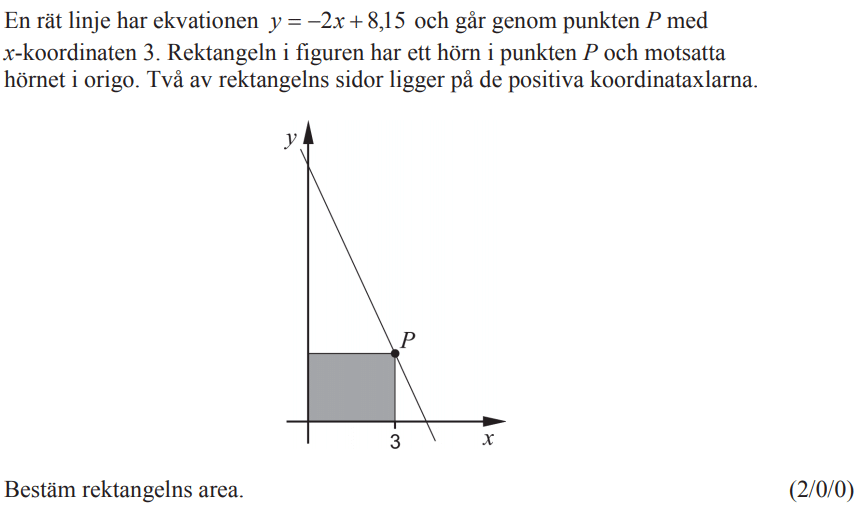
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 1).
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 14).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 1).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 1).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 4).
Fler uppgifter finns här:
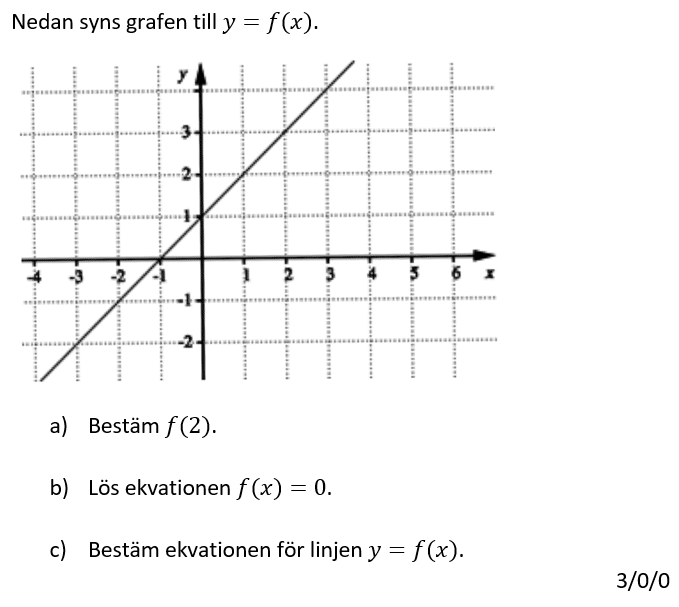
2.2 Funktioner och f(x)
Checklista
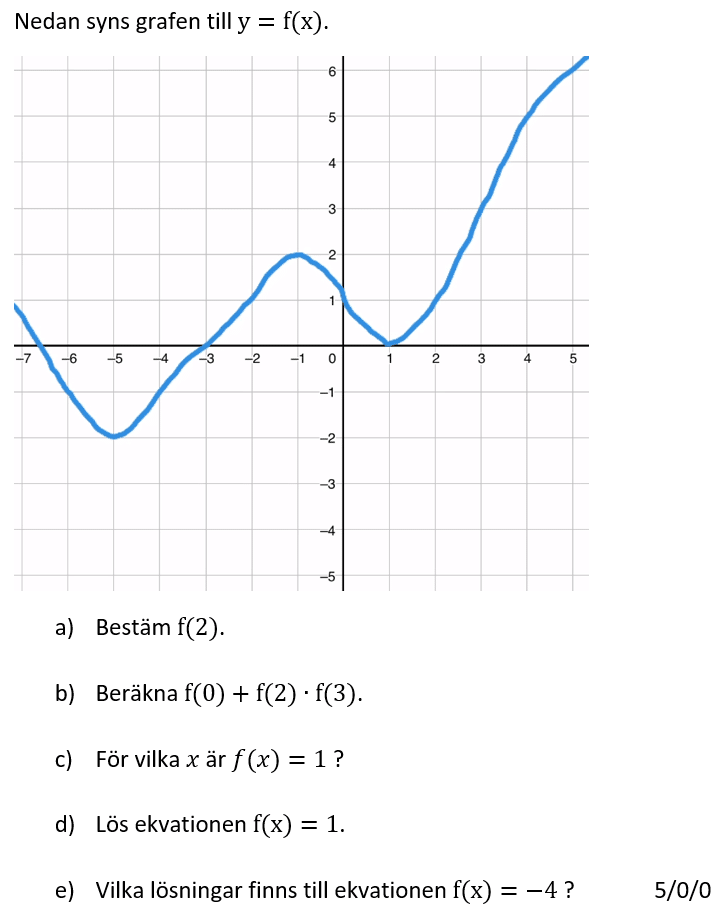
- Förstå att f(x) innebär ett y-värde (funktionsvärde) och att det som står inuti parentesen innebär x-värdet. Om uppgiften handlar om andra variabler kanske det står s(t) istället eller liknande.
- Kunna bestämma f(4)
- algebraiskt med hjälp av funktionen.
- med hjälp av grafen till funktionen.
- Kunna lösa ekvationen f(x)=3
- algebraiskt med hjälp av funktionen.
- med hjälp av grafen till funktionen.
- Förstå innebörden i om det står f(2a) och funktionen är f(x)=x+1. Att x ska bytas mot 2a.
Viktigaste genomgångarna
Vad är en funktion och hur fungerar f(x) ?
Ytterligare exempel med f(x)
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från egen genomgång.
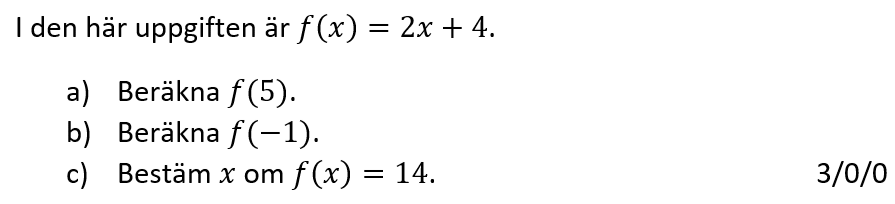
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 3).
Löses utan digitala hjälpmedel. Från HT 2012 och HT 2016 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 7).
Fler uppgifter finns här:
3 Ekvationssystem
3.1 Grafisk lösning
Grafisk lösning för hand, samt med dator eller grafritande räknare
Checklista
- Grafisk lösning av ekvationssystem
- för hand (rita linjerna, ta reda på skärningspunkten)
- med Geogebra (eller annat digitalt verktyg)
Viktigaste genomgångarna
Lösa ett ekvationssystem grafiskt, både för hand och med digitalt verktyg (GeoGebra).
Programmet Desmos fungerar på samma sätt som GeoGebra, om du har tillgång till detta.
Uppgifter med videoförklaringar
OBS: Det står på de flesta av dessa uppgifter att du ska lösa dem utan digitala hjälpmedel, men välj några av dem att lösa i GeoGebra istället!
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
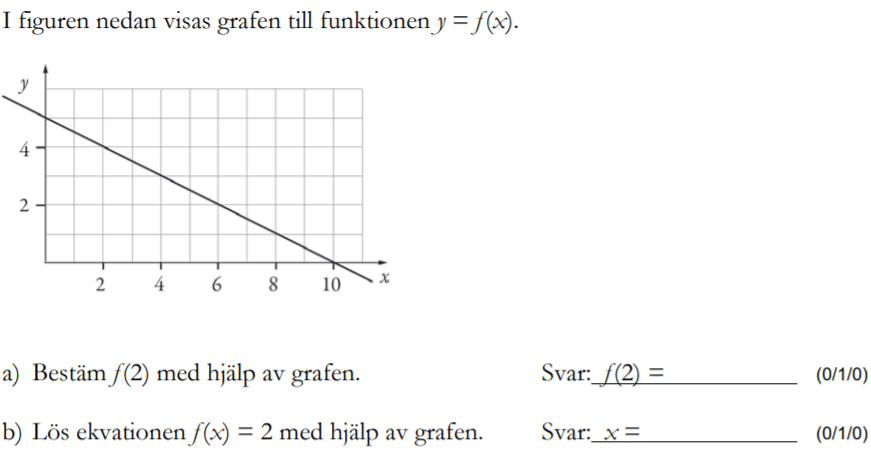
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 3).
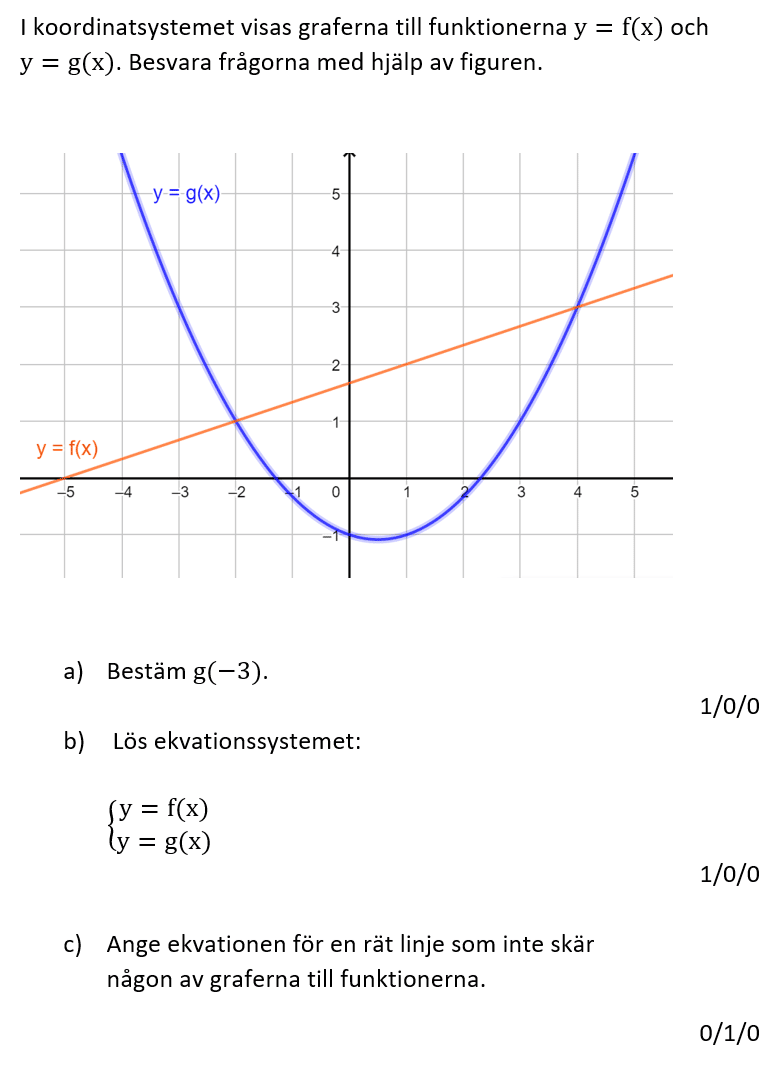
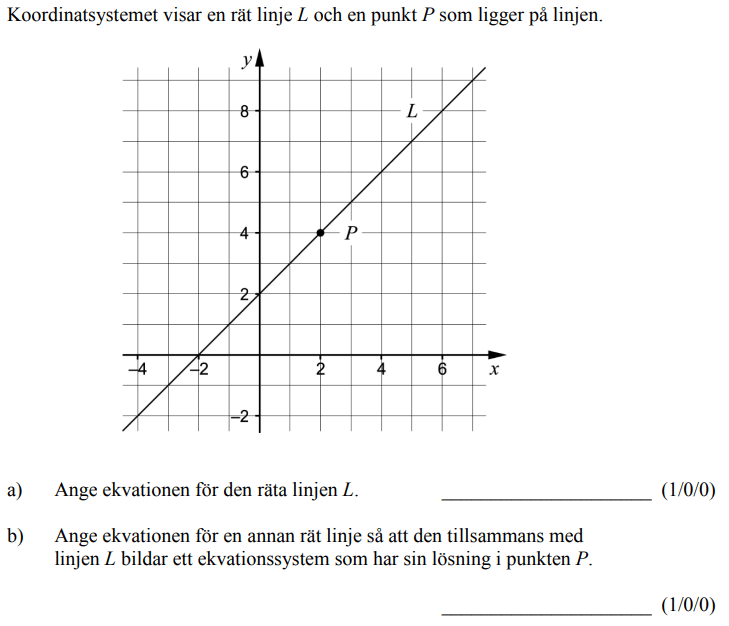
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Fler uppgifter finns här:
3.2 Algebraisk lösning
3.2.1 Additionsmetoden
Checklista
- Kunna lösa ett ekvationssystem med additionsmetoden
- Ofta behöver någon av ekvationerna (eller båda) förlängas innan de kan adderas med varandra.
- Kunna kontrollera att lösningen stämmer.
Viktigaste genomgångarna
Genomgång om additionsmetoden
Liknande genomgång
Uppgifter med videoförklaringar
Uppgifter där additionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Uppgifter där både additionsmetoden och substitutionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.
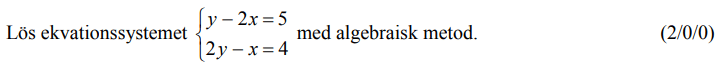
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 11).
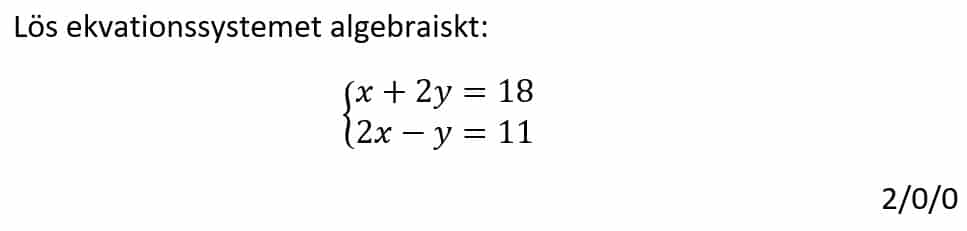
Löses utan digitala hjälpmedel.
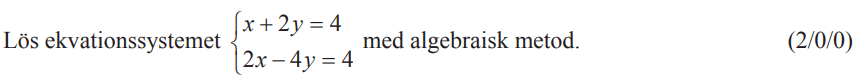
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 12).
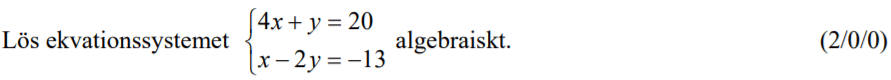
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 12).
Fler uppgifter finns här:
3.2.2 Substitutionsmetoden
Checklista
- Kunna lösa ett ekvationssystem med substitutionsmetoden.
- Ofta behöver du börja med att lösa ut någon variabel från en av ekvationerna.
- Kunna kontrollera att lösningen stämmer.
Viktigaste genomgångarna
Genomgång om substitutionsmetoden
Liknande genomgång
Uppgifter med videoförklaringar
Uppgifter där substitutionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Uppgifter där både additionsmetoden och substitutionsmetoden används i videoförklaringarna.
Du väljer själv när du använder substitutionsmetoden eller additionsmetoden. Prova göra alla uppgifter med den metod som du väljer.
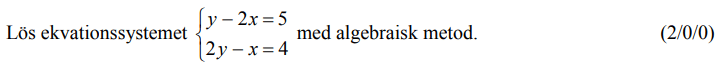
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 11).
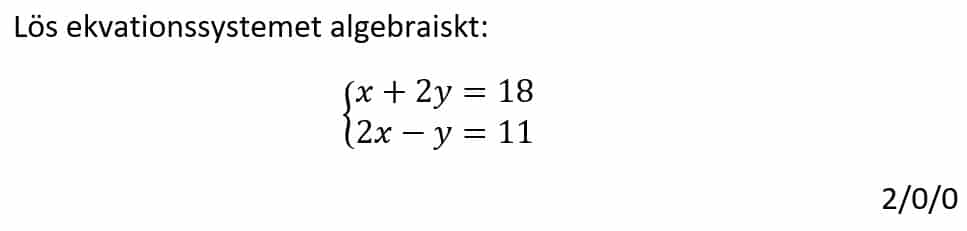
Löses utan digitala hjälpmedel.
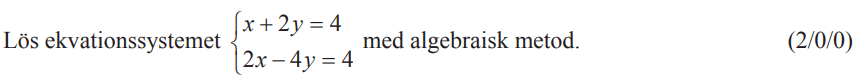
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 12).
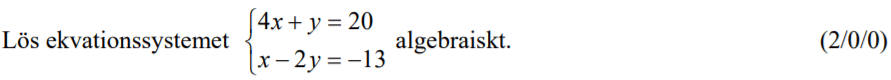
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 12).
Fler uppgifter finns här:
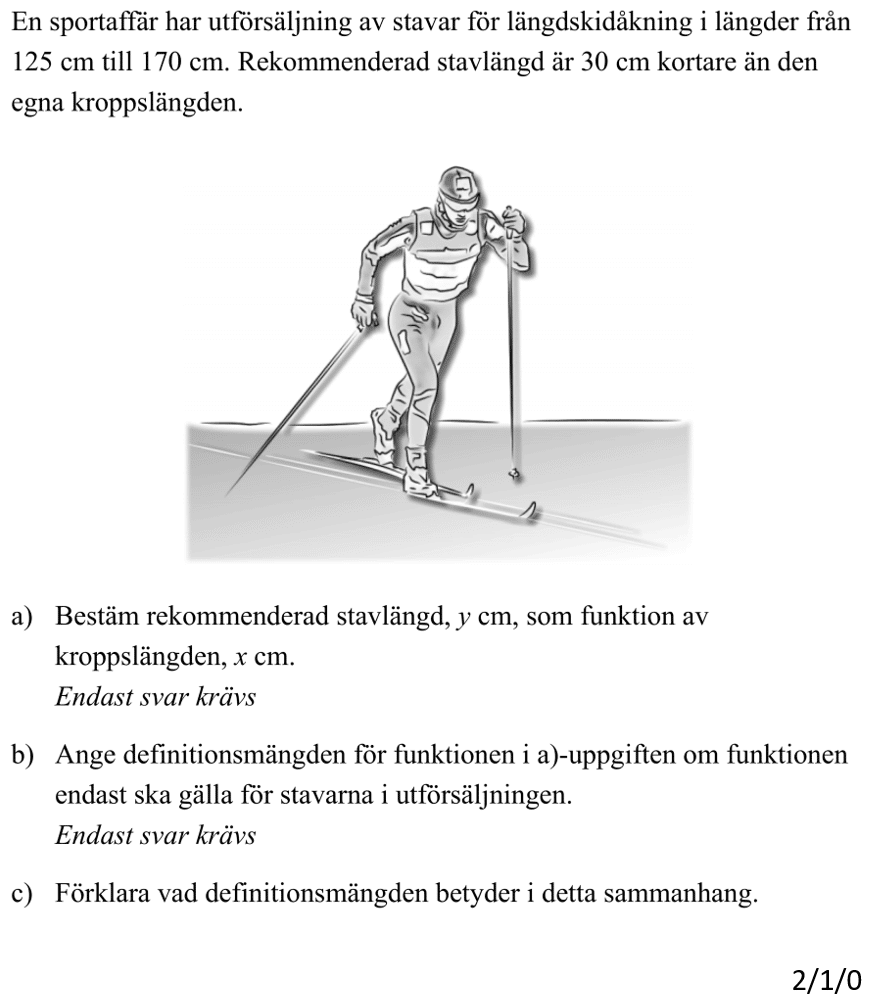
3.3 Tillämpningar
Checklista
- Kunna ställa upp ett ekvationssystem utifrån en textuppgift (”verklig situation”).
- Vara noga med att definiera variablerna, att berätta vad x och y innebär i det sammanhang som uppgiften handlar om.
- Kunna lösa ekvationssystemet med valfri metod. Ofta kan GeoGebra spara mycket tid.
- Vara noga med att svara på själva frågan.
Viktigaste genomgångarna
Exempeluppgift som först löses med GeoGebra och därefter även för hand
Den första uppgiften i videon.
Exempeluppgift som löses för hand
En till exempeluppgift som löses för hand
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 7).
Kommentar: I uppgiften löser jag ekvationssystemet med substitutionsmetoden, men det går lika bra att använda någon av de andra metoderna, inklusive grafisk lösning med digitalt hjälpmedel.
Fler uppgifter finns här:
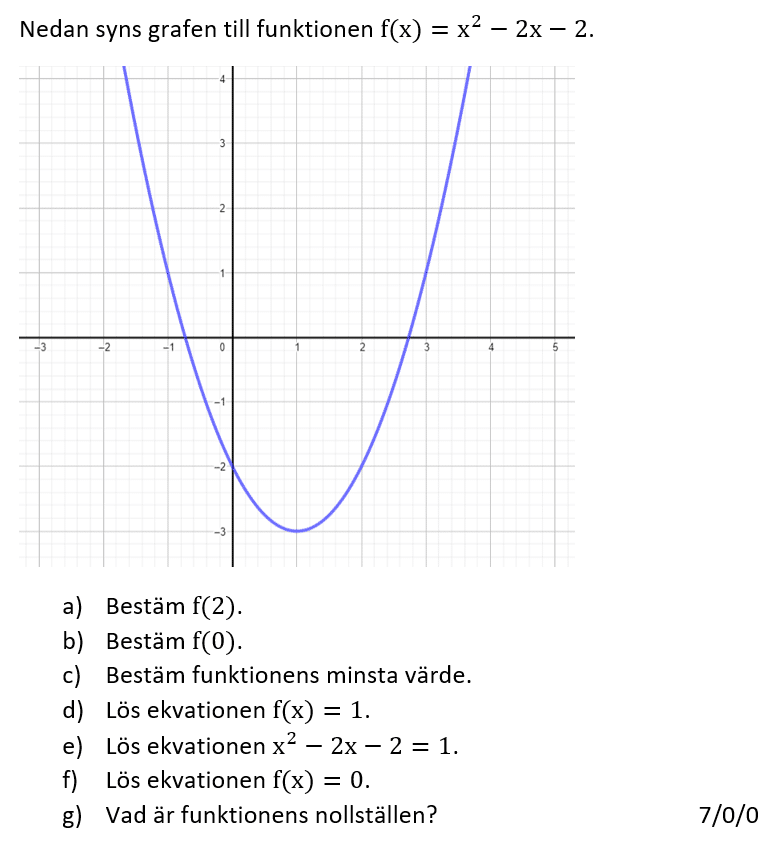
4. Andragradsuttryck
4.1 Parentesregler
Multiplikation av parenteser, kvadreringsreglerna, konjugatregeln och faktorisering
Checklista
Viktigaste genomgångarna
Multiplikation av två parenteser
Kvadreringsreglerna och konjugatregeln på formelbladet
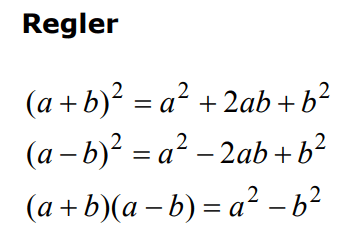
Kvadreringsreglerna och konjugatregeln
Uppgifter med videoförklaringar
Från formelbladet:
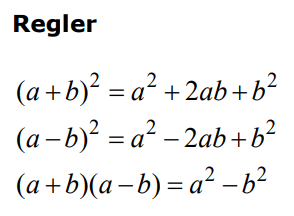
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 9).
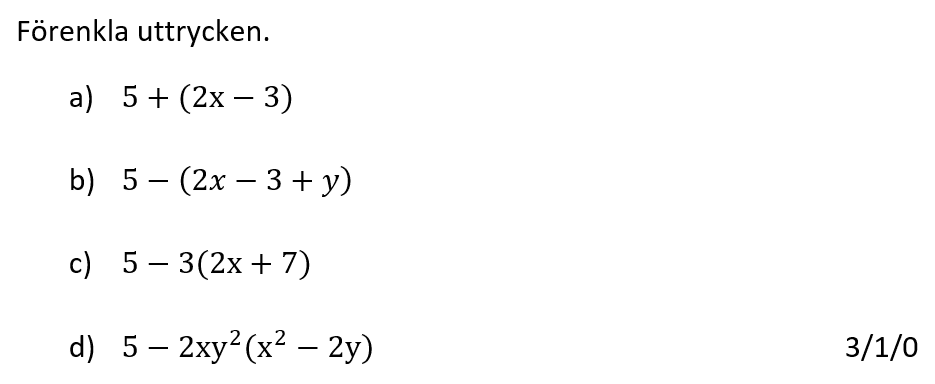
Löses utan digitala hjälpmedel. Från egen genomgång.
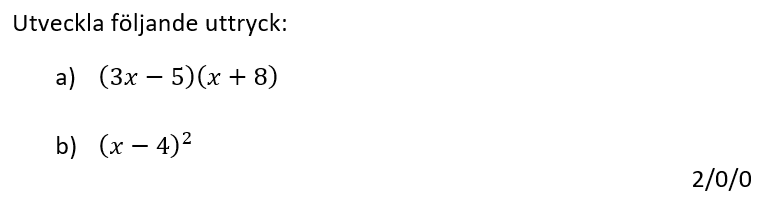
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 1).
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 1).
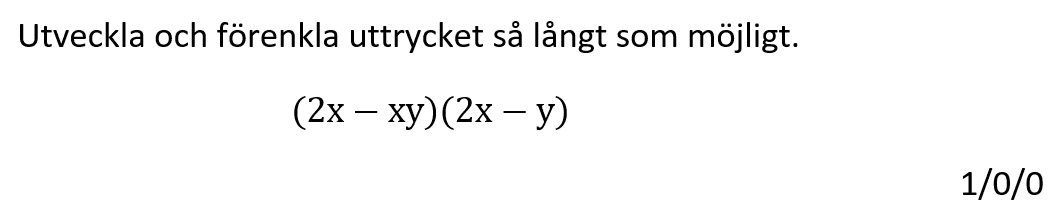
Löses utan digitala hjälpmedel.
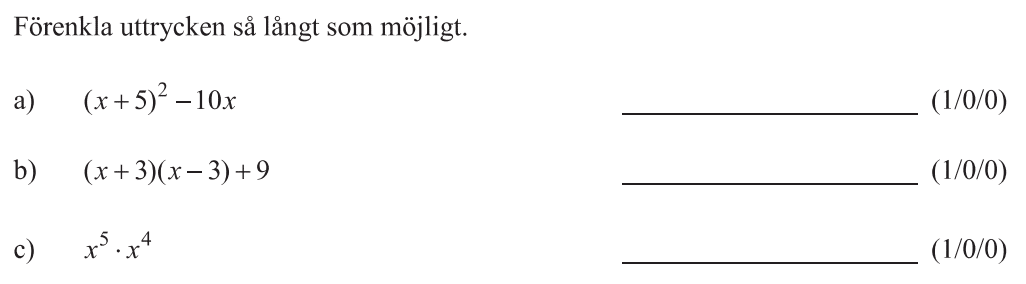
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a).
Bedömningsanvisningar/facit (uppgift 2).
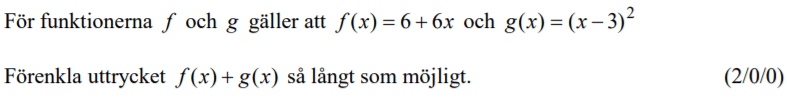
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 9).
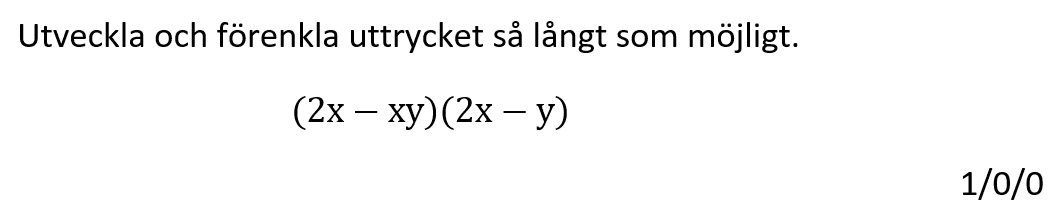
Löses utan digitala hjälpmedel.
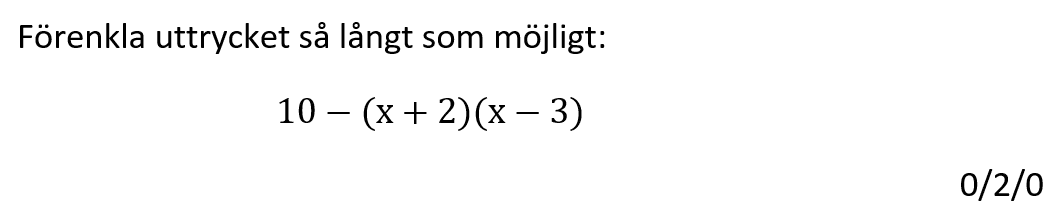
Löses utan digitala hjälpmedel.
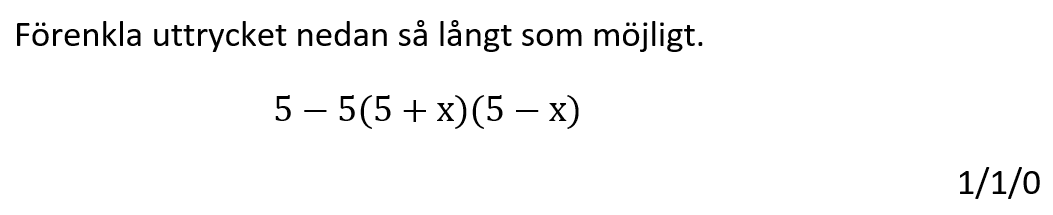
Löses utan digitala hjälpmedel.
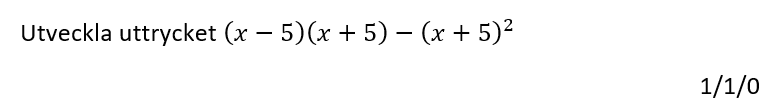
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 7).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 5).
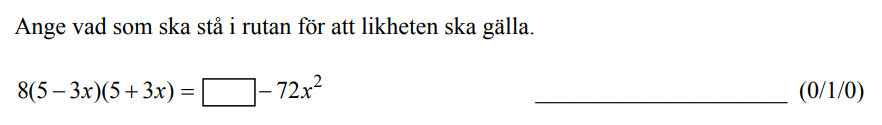
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 2a).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 6).
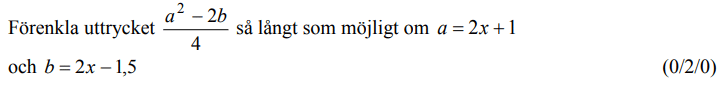
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 13).
Fler uppgifter finns här:
4.2 Andragradsekvationer
Checklista
Från formelbladet:
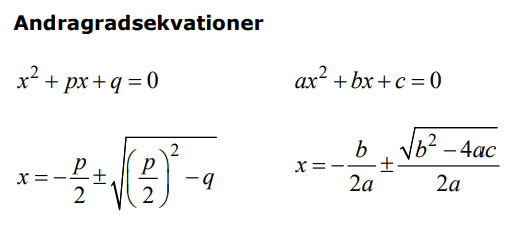
Viktigaste genomgångarna
Val av metod (viktigt)
Metod 1: Rotmetoden (Kvadratrotsmetoden)
Metod 2: Nollproduktmetoden (faktorisering)
Metod 3: Lösningsformeln (pq-formeln)
Uppgifter med videoförklaringar
Från formelbladet:
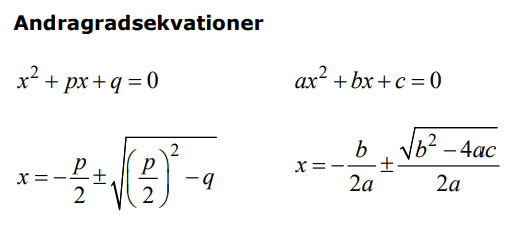
Löses utan digitala hjälpmedel.
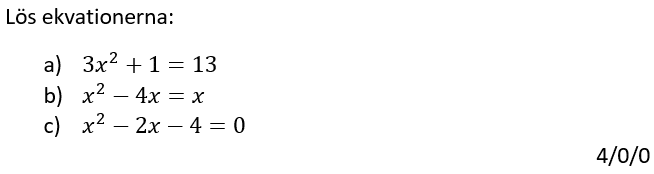
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 10).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 10).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 11).
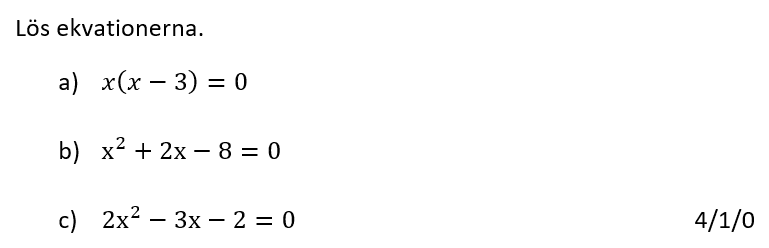
Löses utan digitala hjälpmedel.
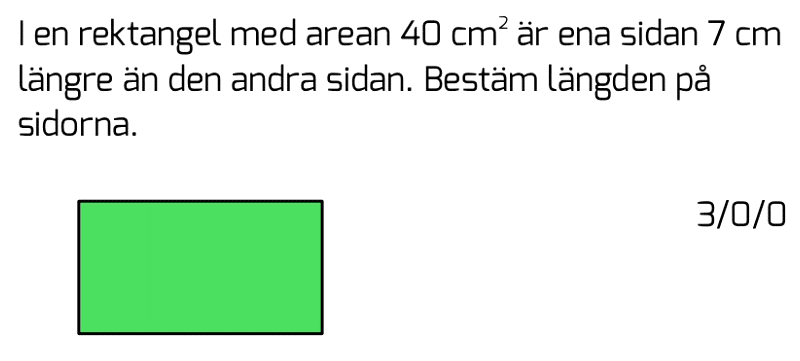
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 10).
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
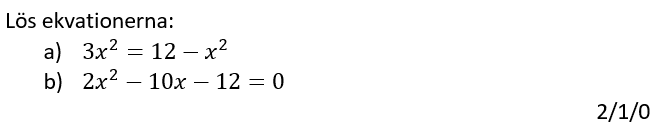
Löses utan digitala hjälpmedel.
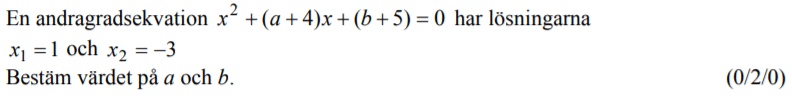
Från VT 2015 (Matematik 2c).
Fler uppgifter finns här:
Svårt?
1. Du måste först välja rätt metod.
2. Sedan kan du börja lösa ekvationen med den metoden.
Metod 1: Rotmetoden (Kvadratrotsmetoden)
Metod 2: Nollproduktmetoden (faktorisering)
Metod 3: Lösningsformeln (pq-formeln)
Enklare uppgifter.
Svårare uppgifter: När det inte blir heltal under rottecknet.
En alternativ formel när det blir knepiga tal under rottecknet: abc-formeln.
4.3 Andragradsfunktioner och grafer
Checklista
Viktigaste genomgångarna
Andragradsfunktioner, förståelse och begrepp
Andragradsfunktioner, beräkningar
Testa själv hur grafen ändras
Dra i ”glidarna” nedan och se hur grafen påverkas!
Uppgifter med videoförklaringar
Från formelbladet:
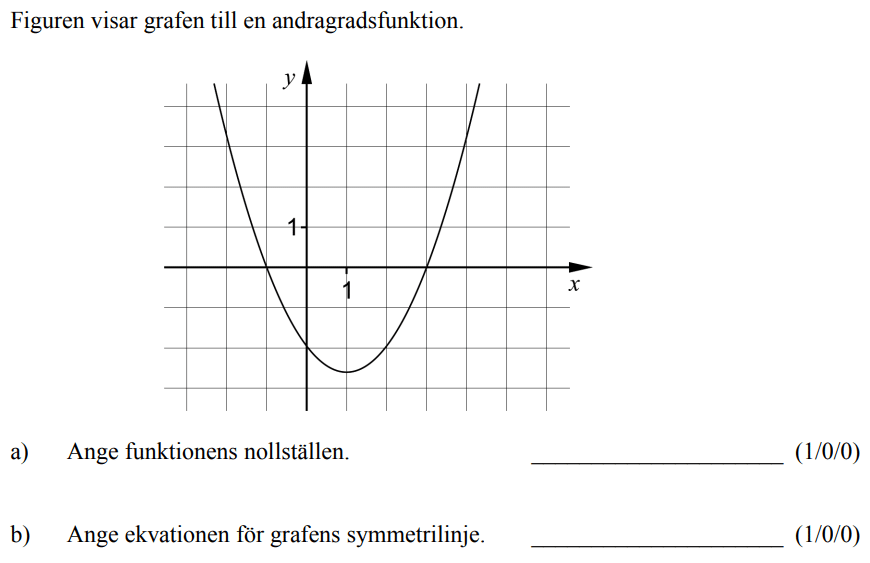
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 1).
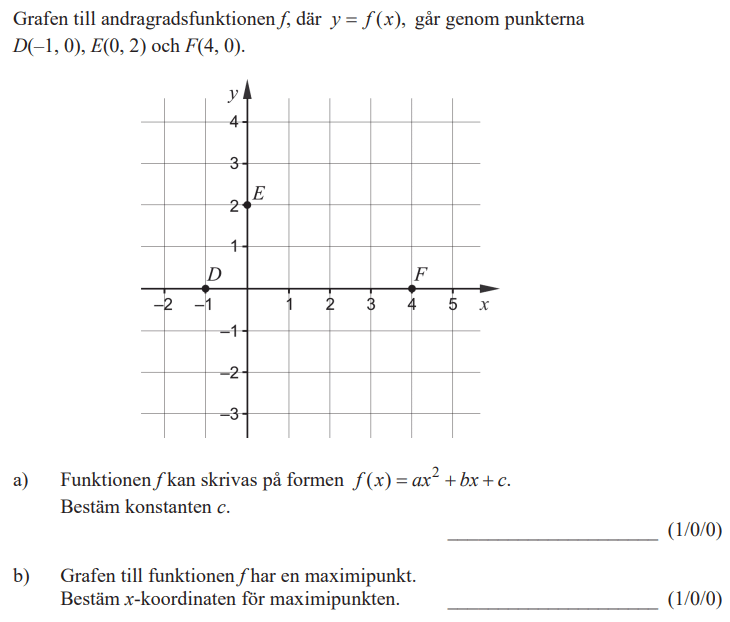
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 2).
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a och 2b).
Bedömningsanvisningar/facit (uppgift 8).
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 19).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 2a).
Bedömningsanvisningar/facit (uppgift 8).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 12).
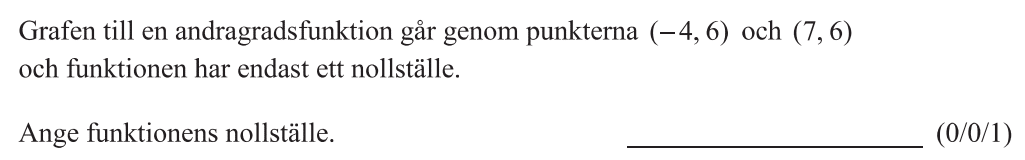
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a).
Bedömningsanvisningar/facit (uppgift 9).
Löses utan digitala hjälpmedel.
Fler uppgifter finns här:
4.4 Tillämpningar
Checklista
Viktigaste genomgångarna
När du får använda GeoGebra:
Lös snabbt uppgifter med andrgradsfunktioner i Geogebra
Relevant är främst uppgifterna med E- och C-poäng. I det här området är det ganska enkelt att klara även C-uppgifterna om du kan programmet skapligt.
När du måste lösa uppgifterna för hand:
Genomgång med exempeluppgift (kaströrelse)
Kom ihåg:
Klicka på bilden för förstoring.
Uppgifter med videoförklaringar
Från formelbladet:
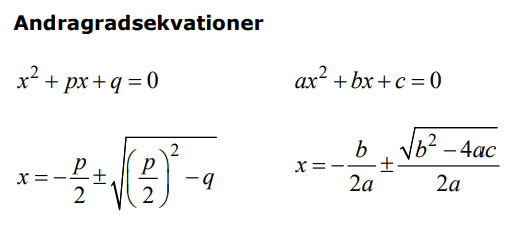
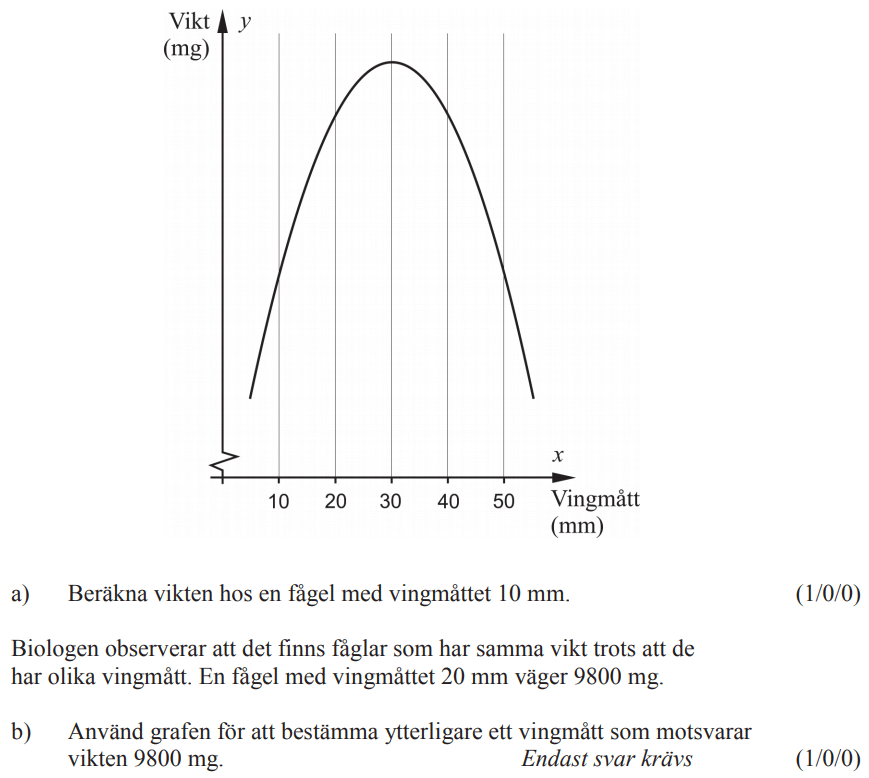
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 15).
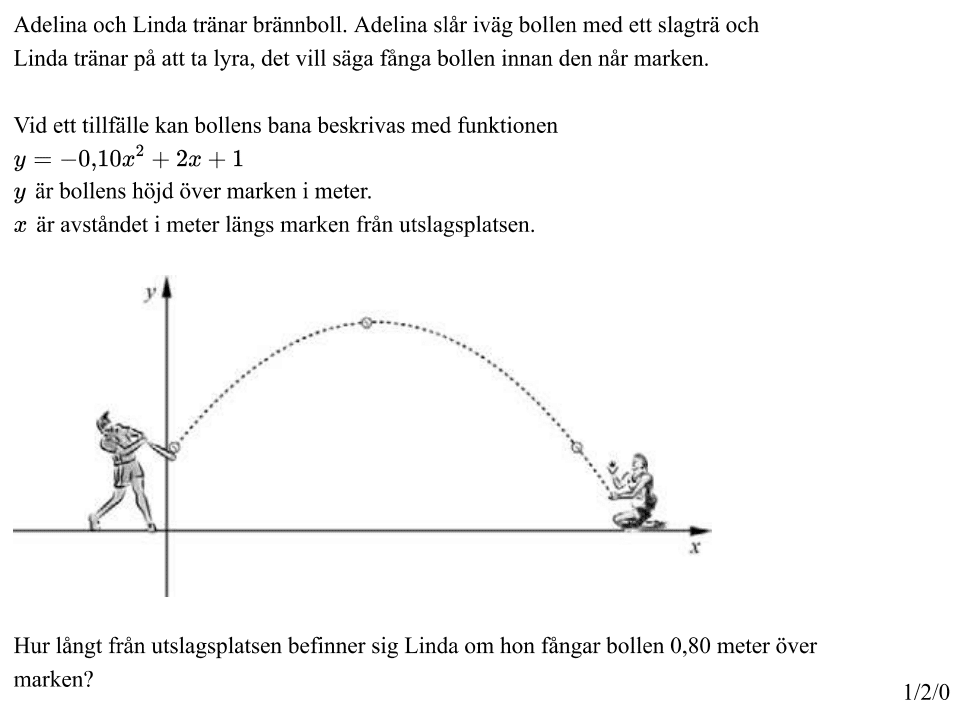
Lånad från kunskapsmatrisen.se.
Kommentar: I videoförklaringen visar jag hur man snabbt kan lösa uppgiften i exempelvis GeoGebra. Samma metod kan användas på grafritande räknare. Jag skriver aldrig ner svaret utan berättar det.
Bedömningsanvisningar/facit (uppgift 1).
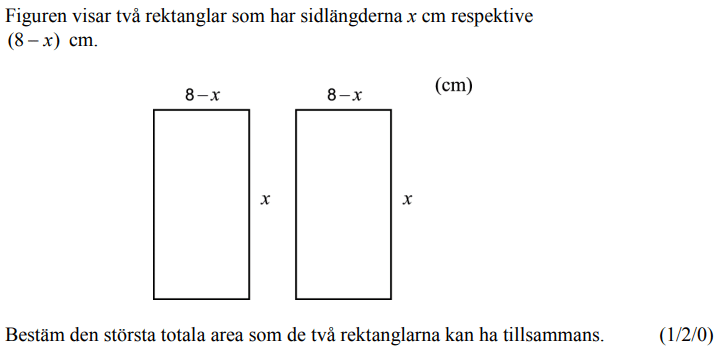
Lånad från kunskapsmatrisen.se.
Kommentar: I videoförklaringen visar jag hur man snabbt kan lösa uppgiften i exempelvis GeoGebra. Samma metod kan användas på grafritande räknare. Jag skriver aldrig ner svaret utan berättar det.
Bedömningsanvisningar/facit (uppgift 2).
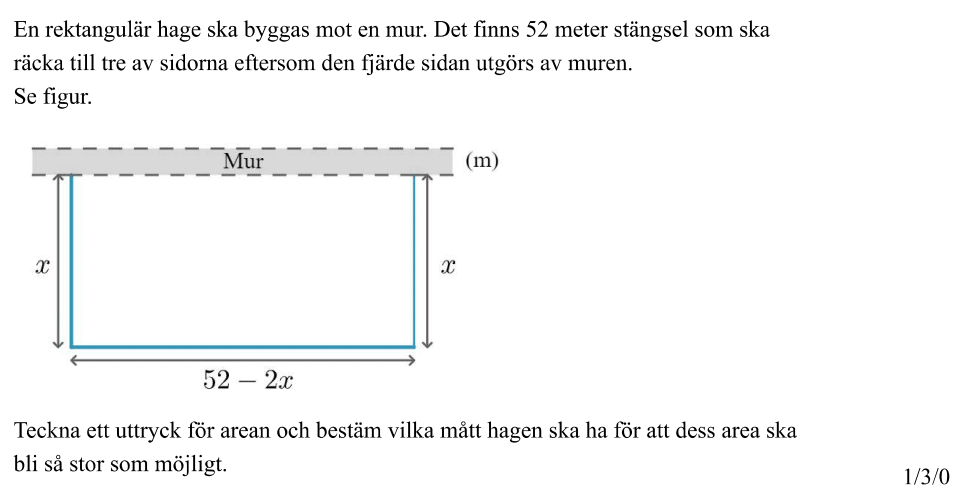
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 7).
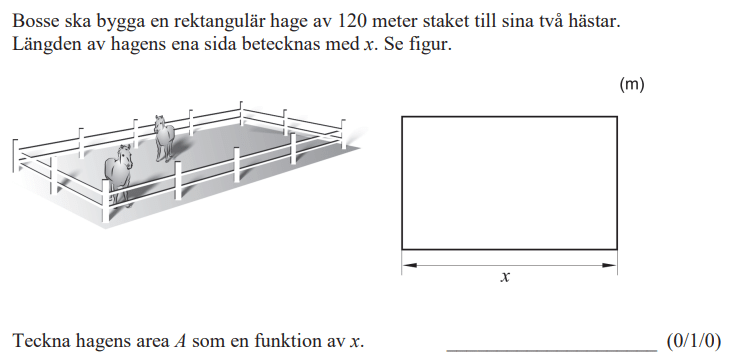
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 12).
Lånad från kunskapsmatrisen.se.
Kommentar: I videoförklaringen visar jag hur man snabbt kan lösa uppgiften i exempelvis GeoGebra. Samma metod kan användas på grafritande räknare. Jag skriver aldrig ner svaret utan berättar det.
Bedömningsanvisningar/facit (uppgift 3).
Fler uppgifter finns här:
5. Potenser, logaritmer och exponentialfunktioner
5.1 Potensregler
Potensregler och regler för rötter (från Matematik 1)
Checklista
Från formelbladet:
Viktigaste genomgångarna
Arbeta med uppgifterna FÖRST och titta på dessa genomgångar vid behov. De är ganska långa.
Grunder: De enklare potensreglerna
En genomgång över alla reglerna
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 1b).
Bedömningsanvisningar/facit (uppgift 3).
Löses utan digitala hjälpmedel. Från egen genomgång.
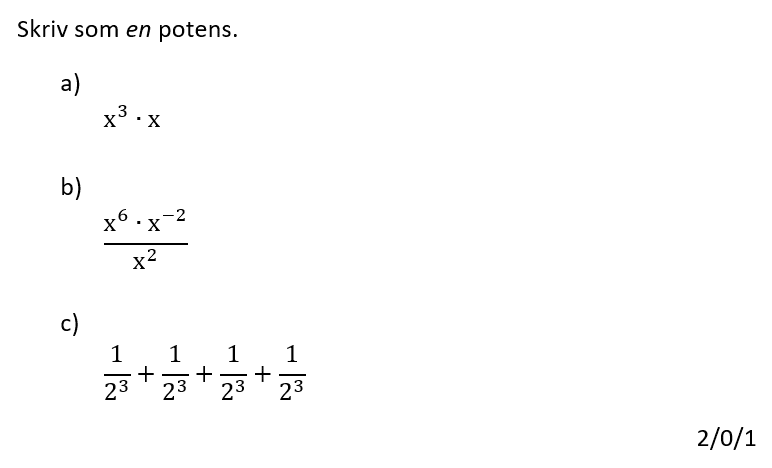
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från egen genomgång.
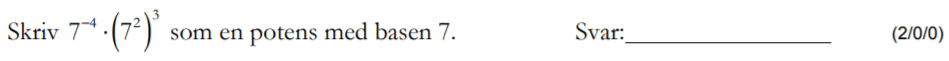
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 2).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 8).
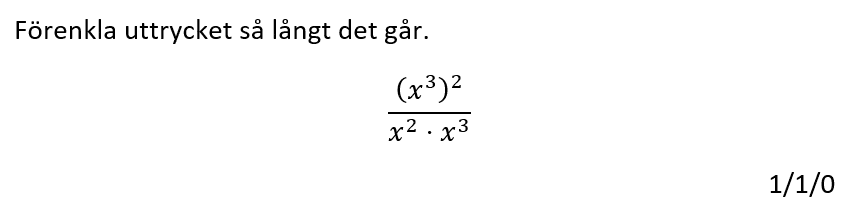
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel.
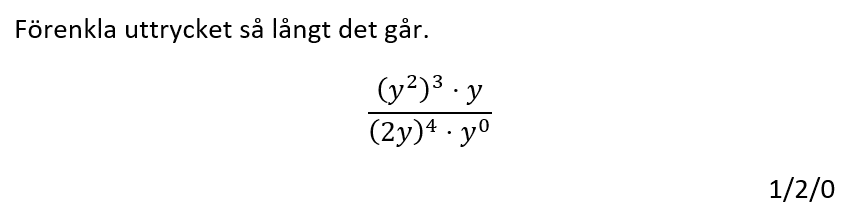
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a).
Bedömningsanvisningar/facit (uppgift 12).
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från egen genomgång.
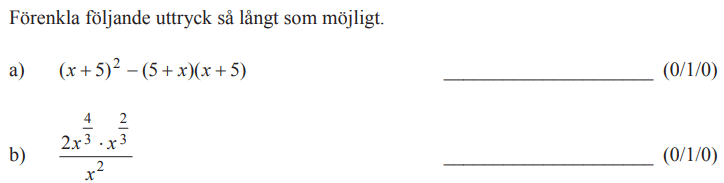
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 5).
Fler uppgifter finns här:
5.2 Exponentialfunktioner mm.
5.2.1 Grunder om exponentialfunktioner (från Matematik 1)
Checklista
Viktigaste genomgångarna
Förändringsfaktor och upprepad procentuell förändring
Exponentialfunktioner. Även med grafisk lösning av exponentialekvation i GeoGebra.
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a).
Bedömningsanvisningar/facit (uppgift 10).
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 3).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 1a, 1b eller 1c).
Bedömningsanvisningar/facit (uppgift 13).
(Svaret i videoförklaringen är inte helt korrekt, då avrundning av förändringsfaktorn gjordes. Se facit nedan).
Kortfattat facit (uppgift 22).
Fler uppgifter finns här:
5.2.2 Potensekvationer (från Matematik 1)
Checklista
Viktigaste genomgångarna
Rötter, potensekvationer och uppgifter med exponentiell förändring
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel. Från egen genomgång.
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1c).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från egen genomgång.
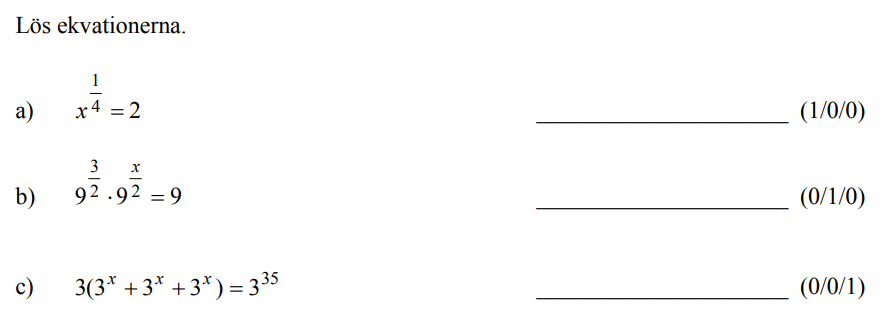
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 2a).
Bedömningsanvisningar/facit (uppgift 5).
5.2.3 Exponentialekvationer med basen 10 samt 10-logaritmer
Checklista
Viktigaste genomgångarna
10-logaritmer och exponentialekvationer med basen 10.
Uppgifter med videoförklaringar
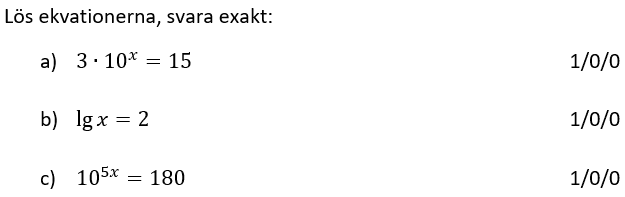
Löses utan digitala hjälpmedel.
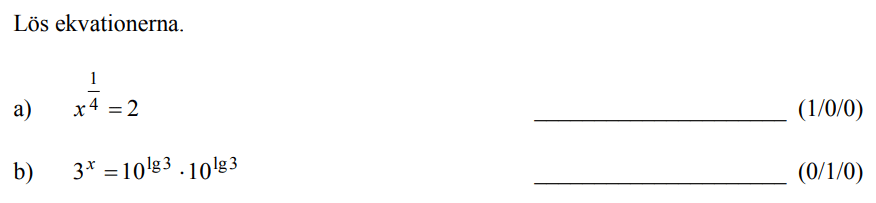
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 5).
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 2).
5.2.4 Lösa exponentialekvationer
Checklista
Viktigaste genomgångarna
Lösa exponentialekvationer
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 2).
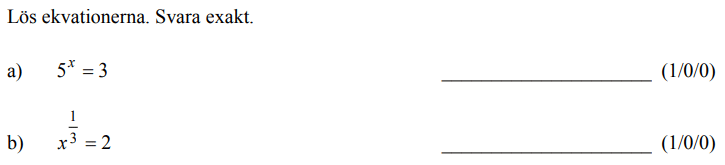
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 2).
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2c).
Bedömningsanvisningar/facit (uppgift 2).
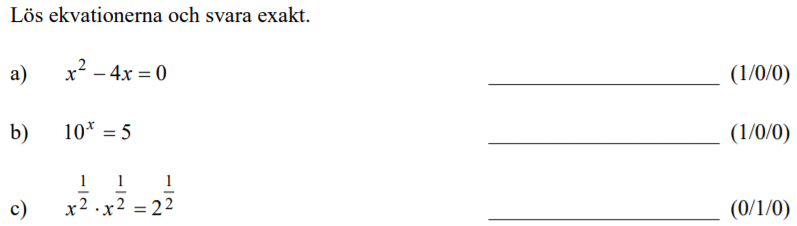
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 3).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 5).
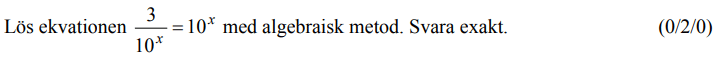
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 14).
Fler uppgifter finns här:
5.2.5 Tillämpningar med GeoGebra
Checklista
Viktigaste genomgångarna
Med GeoGebra:
Tillämpningsuppgift som löses med GeoGebra.
Klippet startar på rätt ställe.
En lite svårare uppgift som blir mycket lättare med GeoGebra
Klippet startar på rätt ställe.
Utan GeoGebra:
Att lösa tillämpningsuppgifter för hand
Detta behöver du ofta inte göra om du har tillgång till GeoGebra.
OBS: På ett ställe i genomgången skriver jag svaret 6 %, men det ska stå 0,6 %.
Uppgifter som löses med GeoGebra. Fokusera på att lära dig de digitala metoderna om du får använda dator under prov.
Uppgifter med videoförklaringar
Många av dessa uppgifter ser svåra ut, men om du använder GeoGebra och lär dig strategin blir de betydligt enklare.
I Matematik 2a ingår endast lösning med digitalt hjälpmedel, exempelvis GeoGebra.
Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 17).
I Matematik 2a ingår endast lösning med digitalt hjälpmedel, exempelvis GeoGebra.
Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 21).
I Matematik 2a ingår endast lösning med digitalt hjälpmedel, exempelvis GeoGebra.
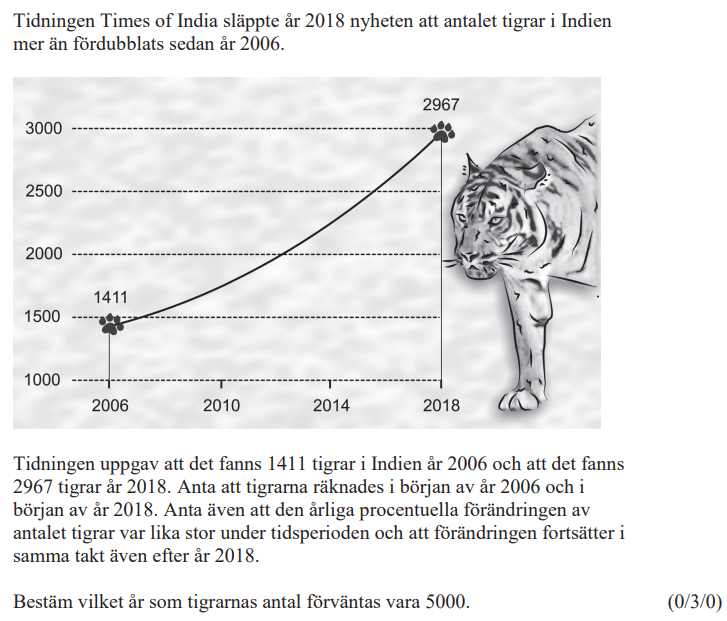
Från VT 2022 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 23).
I Matematik 2a ingår endast lösning med digitalt hjälpmedel, exempelvis GeoGebra.
Från HT 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 22).
I Matematik 2a ingår endast lösning med digitalt hjälpmedel, exempelvis GeoGebra.
Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 22).
I Matematik 2a ingår endast lösning med digitalt hjälpmedel, exempelvis GeoGebra.
Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 20).
5.2.5 Tillämpningar med algebraisk lösning
Checklista
Viktigaste genomgångarna
Med GeoGebra:
Tillämpningsuppgift som löses med GeoGebra.
Klippet startar på rätt ställe.
En lite svårare uppgift som blir mycket lättare med GeoGebra
Klippet startar på rätt ställe.
Utan GeoGebra:
Att lösa tillämpningsuppgifter för hand
Detta behöver du ofta inte göra om du har tillgång till GeoGebra.
OBS: På ett ställe i genomgången skriver jag svaret 6 %, men det ska stå 0,6 %.
Uppgifter som löses med algebraisk metod (för hand). Om du får använda GeoGebra på proven så lägg mer fokus på att lära dig att lösa dem med digitalt verktyg (GeoGebra)
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 3).
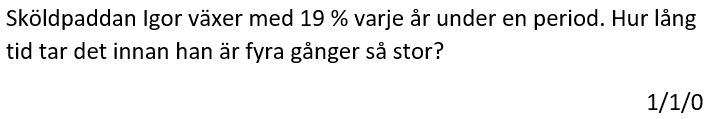
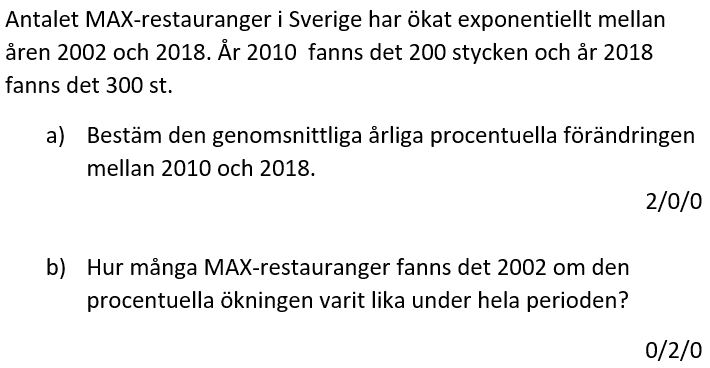
Löses utan digitala hjälpmedel. Från VT 2015 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 7).
6. Geometri och logik
6.1 Avståndsformeln och mittpunktsformeln
Checklista
Viktigaste genomgångarna
Avståndsformeln
Mittpunktsformeln
Videon startar på rätt ställe.
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 5).
6.2 Vinklar
6.2.1 Vinklar och vinkelsatser
Checklista
Viktigaste genomgångarna
Vinklar, namn på vinklar, vinkelsumma och olika satser
Uppgifter med videoförklaringar saknas än så länge
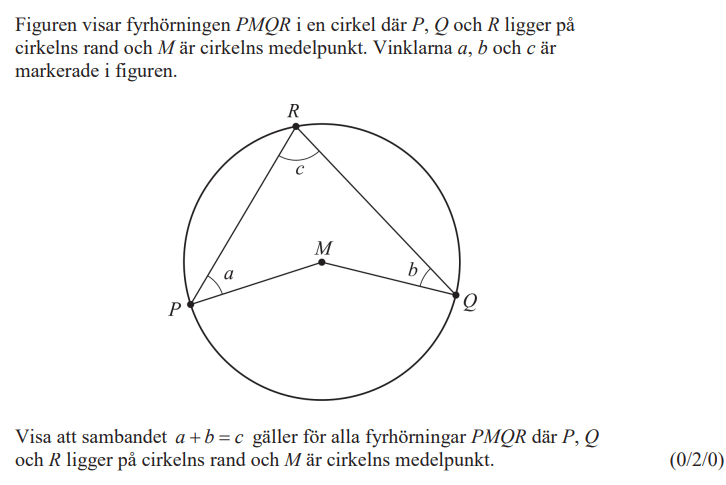
6.2.2 Randvinkelsatsen
Checklista
Viktigaste genomgångarna
Randvinkelsatsen och följdsatser
Uppgifter med videoförklaringar
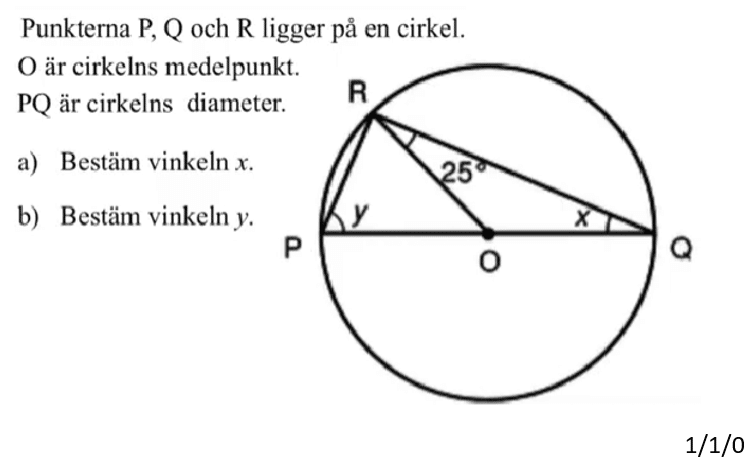
Löses utan digitala hjälpmedel.
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 11).
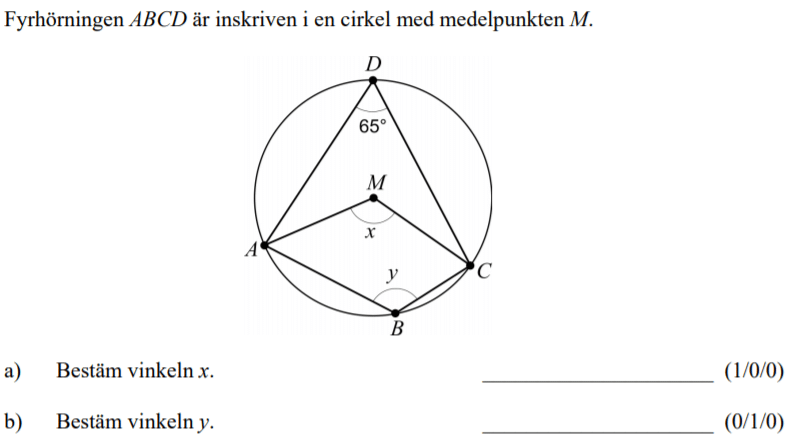
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 6).
Fler uppgifter finns här:
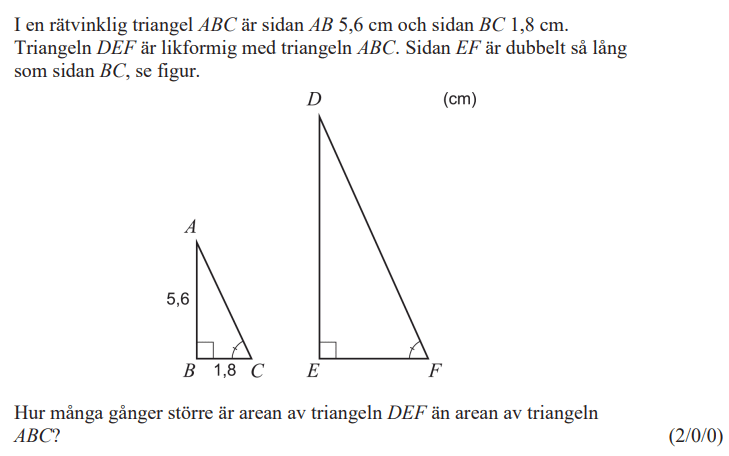
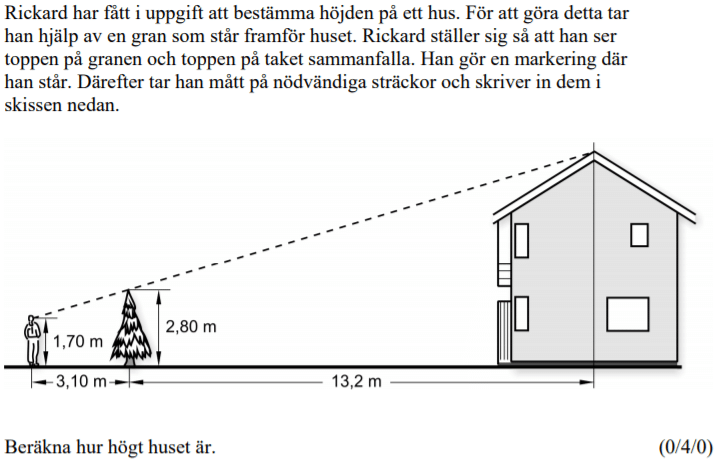
6.3 Likformighet och kongruens
Checklista
Viktigaste genomgångarna
Likformighet
Inte lika vanligt på enklare uppgifter:
Topptriangelsatsen, transversalsatsen och bisektrissatsen
Kongruens
Uppgifter med videoförklaringar
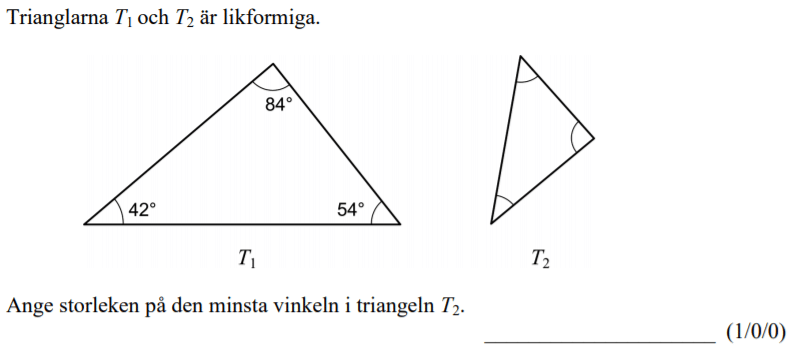
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 3).
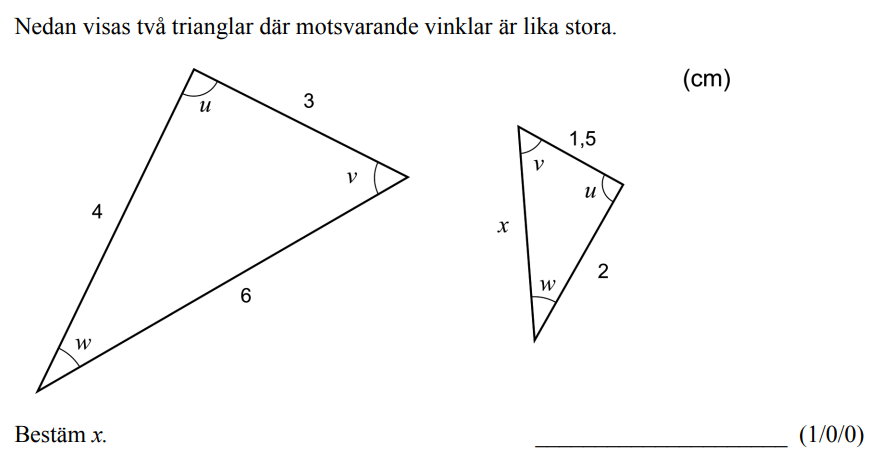
Löses utan digitala hjälpmedel. Från HT 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 2).
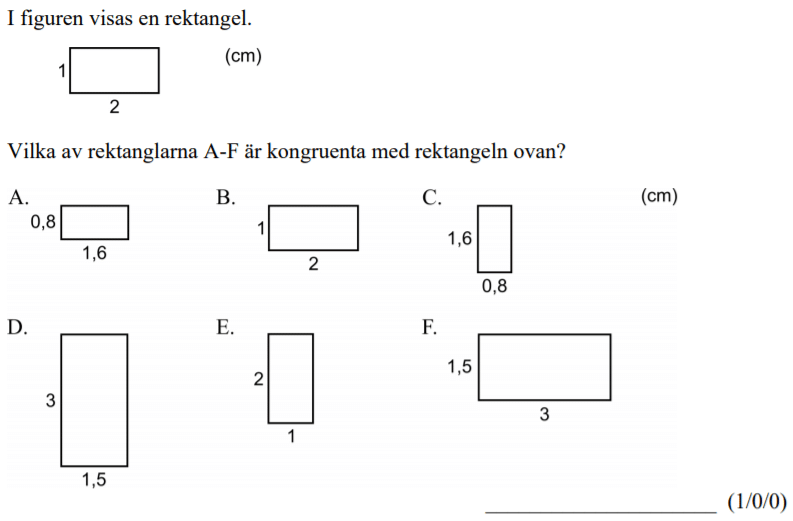
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 2).
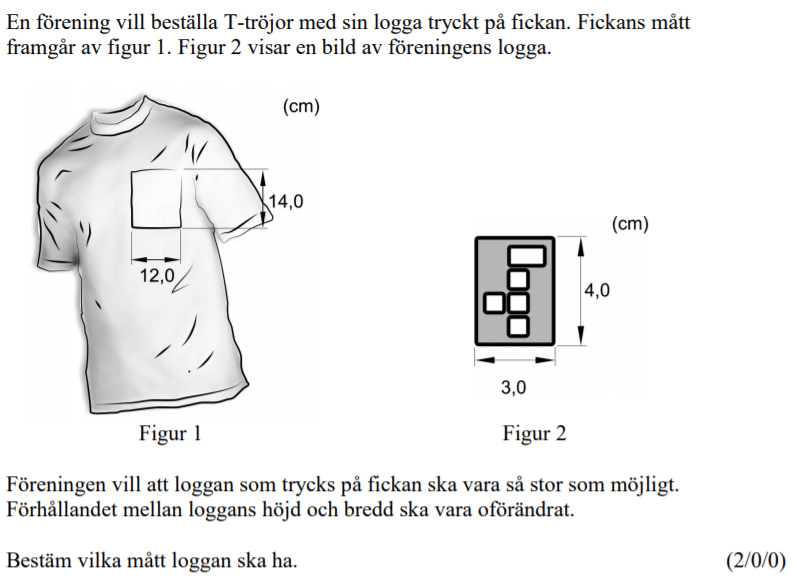
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 11).
Fler uppgifter finns här:
6.4 Logik (implikation och ekvivalens) och bevis
Checklista
Viktigaste genomgångarna
Implikation och ekvivalens
Uppgifter med videoförklaringar
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 3).
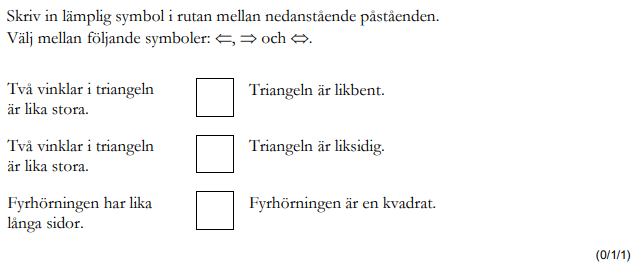
Löses utan digitala hjälpmedel. Från VT 2014 (Matematik 1b).
Bedömningsanvisningar/facit (uppgift 13).
Löses utan digitala hjälpmedel. Från HT 2016 (Matematik 1a, 1b,eller 1c).
Bedömningsanvisningar/facit (uppgift 3).
7. Statistik
7.1 Lägesmått, lådagram och andra begrepp
Checklista
Viktigaste genomgångarna
Lägesmått: Medelvärde, median och typvärde
Lådagram, median, kvartilavstånd, variationsbredd, percentiler
Statistik i GeoGebra (går snabbt!)
Median, medelvärde, kvartilavstånd, variationsbredd, lådagram
Uppgifter med videoförklaringar
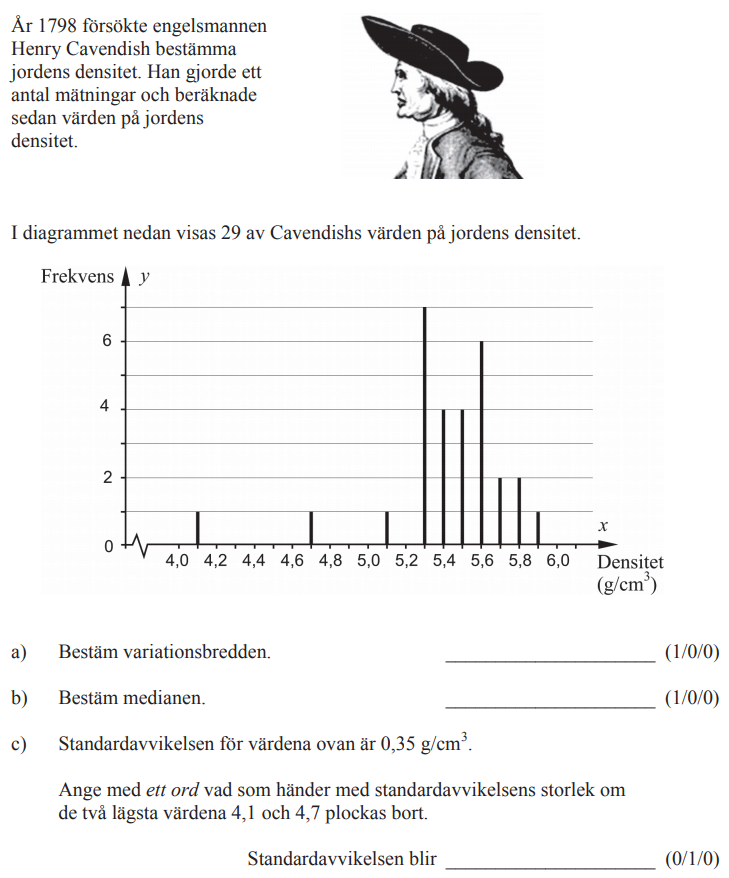
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 4).
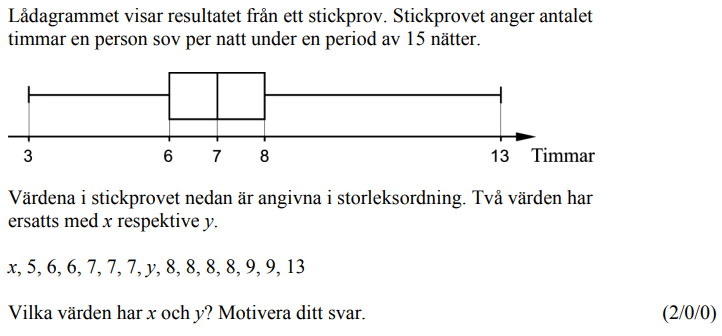
Från VT 2015 (Matematik 2a, 2b eller 2c).
7.2 Standardavvikelse och normalfördelning
Checklista
Viktigaste genomgångarna
Om du redan har lite koll på begreppet normalfördelning:
Hur räknar vi normalfördelning i GeoGebra?
Om du inte har koll på begreppet normalfördelning:
Vad är standardavvikelse och normalfördelning?
En liten text skriven av ChatGPT med ganska tydligt exempel:
Standardavvikelse
Tänk dig att du har en butik och du mäter skostorleken på varje kund under en månad. Efter att ha mätt alla, räknar du ut genomsnittet. Standardavvikelse visar hur mycket varje kunds skostorlek skiljer sig från detta genomsnitt.
Om de flesta av dina kunder har skostorlekar som är väldigt nära genomsnittet, är standardavvikelsen låg. Det betyder att det inte finns så stor skillnad i skostorlekar bland dina kunder. Å andra sidan, om du har många kunder med väldigt små eller väldigt stora fötter jämfört med genomsnittet, är standardavvikelsen hög. Det indikerar en större variation i skostorlekar.
Normalfördelning
Normalfördelning är ett vanligt mönster som ofta uppkommer i många olika sammanhang, som skostorlekar. Om du ritar upp en graf med antalet kunder mot deras skostorlekar, skulle du sannolikt se att de flesta kunder har skostorlekar nära medelvärdet, och färre kunder har mycket små eller mycket stora skostorlekar.
Denna graf skulle se ut som en kulle – högst i mitten där de vanligaste skostorlekarna finns, och lägre på sidorna för de ovanliga, mycket små eller mycket stora storlekarna. Detta illustrerar normalfördelningen: de flesta värden (här skostorlekar) samlas runt medelvärdet, medan extremvärden är sällsynta.
Hur standardavvikelse och normalfördelning hänger ihop
När data är normalfördelad, som vi antar att skostorlekarna är i detta exempel, kan standardavvikelsen användas för att förstå hur data är spridda runt medelvärdet.
Bestämmer vanligaste värden: I en normalfördelning ligger cirka 68% av alla värden (här skostorlekar) inom en standardavvikelse från medelvärdet. Det betyder att om genomsnittlig skostorlek är 42 och standardavvikelsen är 2, skulle de flesta av dina kunder (ungefär 68%) ha skostorlekar mellan 40 och 44.
Identifierar extremvärden: Om du går längre ut – säg två eller tre standardavvikelser från medelvärdet – omfattar du ännu fler värden, men som inte är lika vanliga. Cirka 95% av värdena ligger inom två standardavvikelser, och 99,7% inom tre standardavvikelser. Detta hjälper dig att förstå hur ovanliga extremt små eller stora skostorlekar är.
Uppgifter med videoförklaringar
Viktig kommentar:
I flera av uppgifterna nedan har värden valts så att de ska gå att lösa med hjälp av normalfördelningskurvan på formelbladet. Sedan något år tillbaka ingår det dock att uppgifterna ska lösas med digitala verktyg, så du bör räkna med att Skolverket framöver kommer välja uppgifter där digitala verktyg krävs.
I första uppgiften om kanelsnäckorna skulle det exempelvis kunna vara att du ska tala om hur många som förväntas väga mer än 87 gram. Detta går inte med hjälp av formelbladet eftersom det endast finns hela standardavvikelser där.
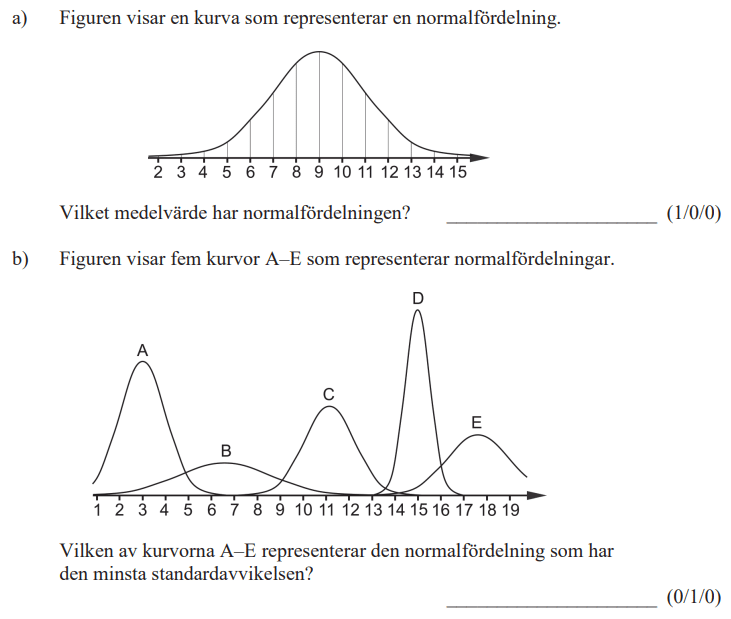
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2a, 2b och 2c).
Bedömningsanvisningar/facit (uppgift 4).
Löses utan digitala hjälpmedel. Från vt 2014 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 4).
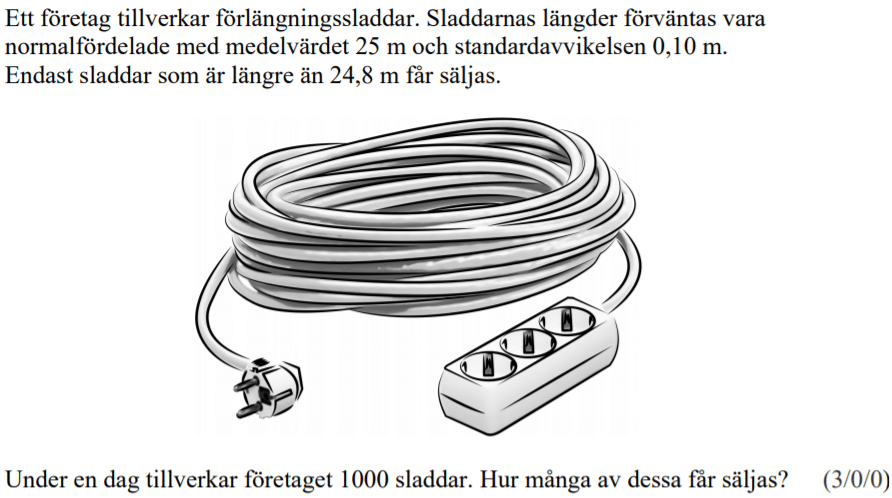
Löses utan digitala hjälpmedel. Från HT 2012 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 13).
Löses utan digitala hjälpmedel. Från HT 2013 (Matematik 2b och 2c).
Bedömningsanvisningar/facit (uppgift 5).
Från HT 2013 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 24).
Kommentar: Uppgiften är från Matematik 4, men samma uppgift kan även komma i Matematik 2. Videoförklaringen startar vid det tillfälle där jag visar hur man gör i GeoGebra. Metoden som jag visar precis innan ingår inte i Matematik 2.
Från HT 2014 (Matematik 4).
Bedömningsanvisningar/facit (uppgift 25).
Kommentar: Uppgiften är från Matematik 4, men samma uppgift kan även komma i Matematik 2. Videoförklaringen startar vid det tillfälle där jag visar hur man gör i GeoGebra. Metoden som jag visar precis innan ingår inte i Matematik 2.
OBS: I a-uppgiften är standardavvikelsen fel i videon. Detta beror på att cellen för medelvärdet också markerades. Korrekt svar ska vara 16,3.
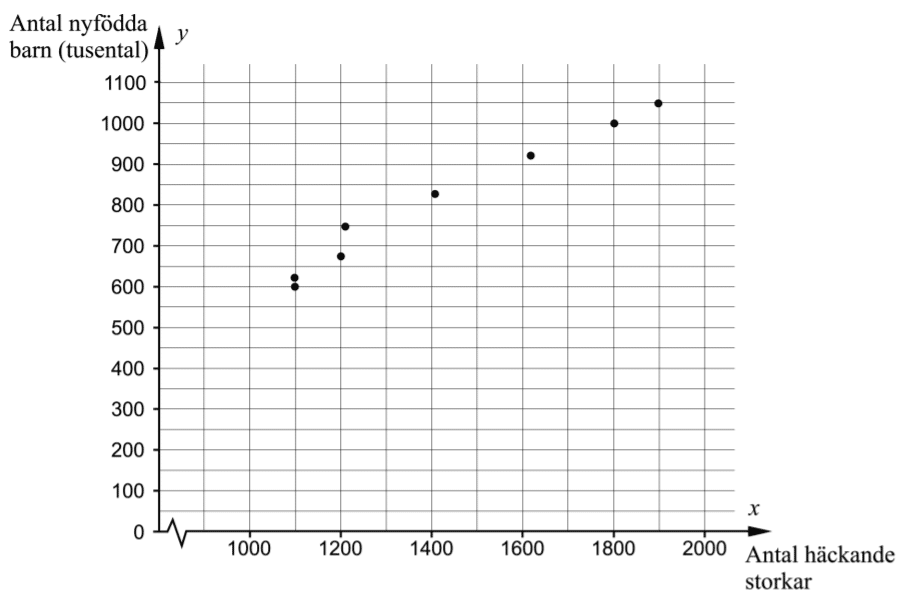
7.3 Regression och korrelationskoefficienten r
Checklista
Viktigaste genomgångarna
Att göra en regression i GeoGebra
Regressionsanalys och korrelationskoefficient
Vad innebär korrelationskoefficienten r och hur beräknar vi denna i GeoGebra och Desmos?
Korrelationskoefficienten r är ett mått på hur stark korrelationen är.
Korrelationskoefficienten r kan anta värden från -1 till 1.
- Om r=1 så ligger alla punkterna samlade på en linje som har positiv lutning. Det är då en mycket stark, positiv korrelation.
- Om r=-1 så ligger alla punkterna samlade på en linje som har negativ lutning. Det är då en mycket stark, negativ korrelation.
- Om r är nära 1 eller -1 så är korrelationen stark.
- Om r är ganska långt ifrån 0, men också långt ifrån 1 eller -1 så är korrelationen svag.
- Om r är nära 0 så är korrelationen mycket svag eller obefintlig.
Exakta gränser finns inte utan är en tolkning från situation till situation om vad som bedöms som stark eller svag.
Stark och positiv korrelation
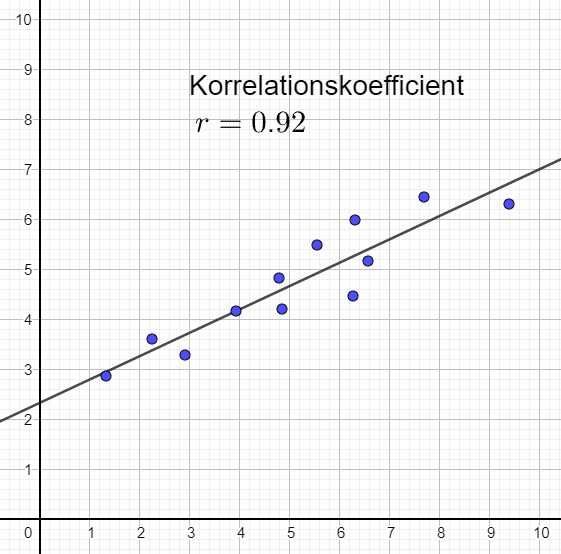
Stark och positiv korrelation
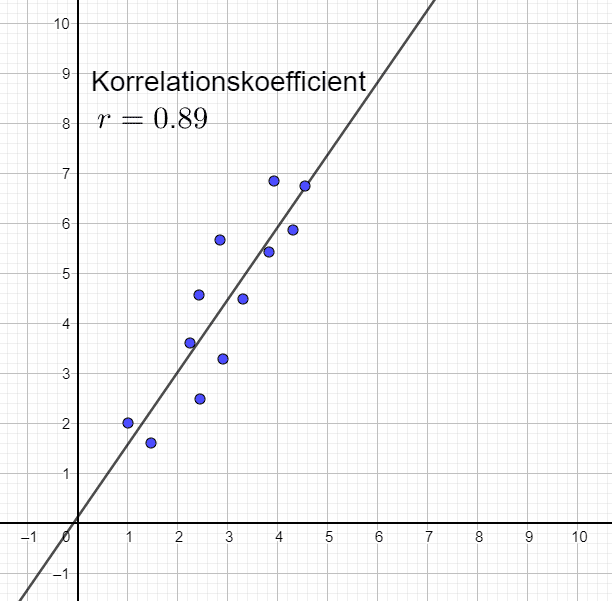
Här lutar linjen brantare än i sambandet till vänster. Hur brant linjen lutar är dock inte avgörande för korrelationskoefficienten r, utan enbart hur väl samlade punkterna är kring linjen, samt om den har positiv eller negativ lutning.
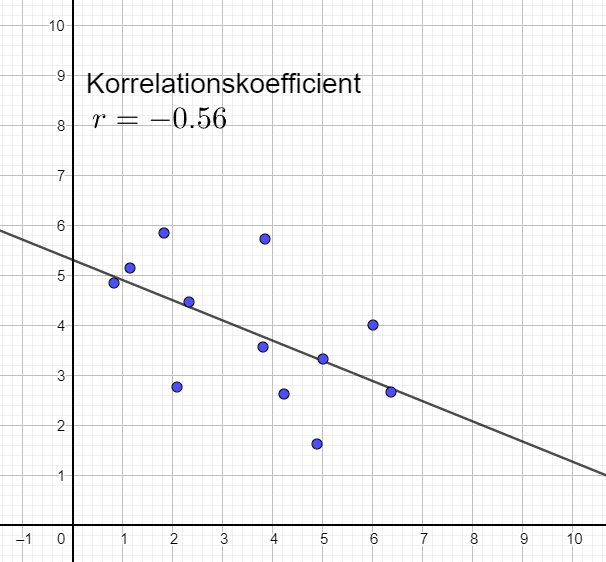
Stark och negativ korrelation
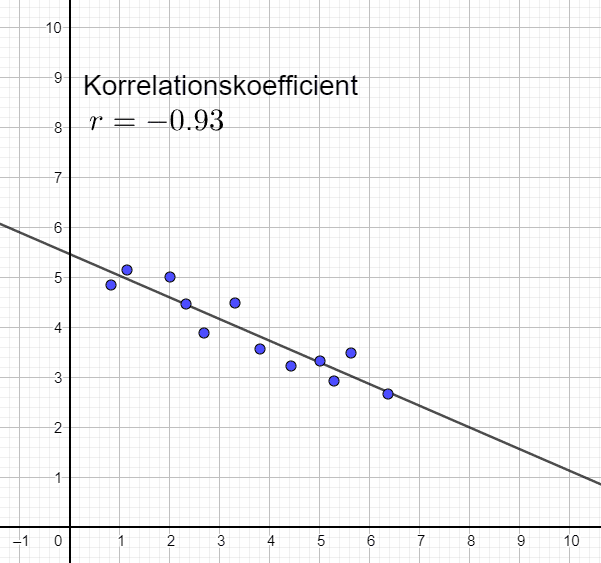
Svag och positiv korrelation
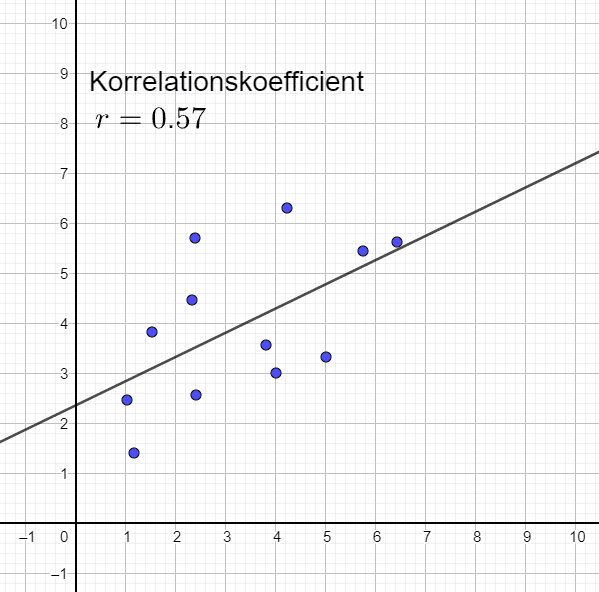
Svag och negativ korrelation
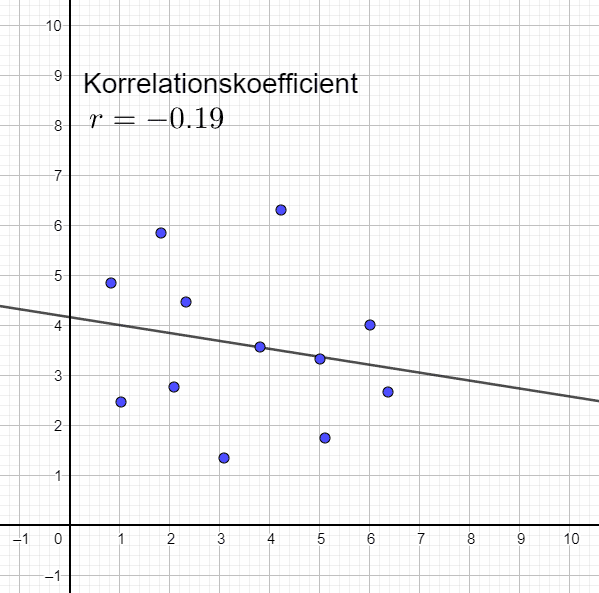
Ingen korrelation (eller ytterst svag och osäker korrelation)
Korrelationskoefficienten visar inte 0, men väldigt nära 0. Eftersom datamängden består av endast ett fåtal punkter är osäkerheten mycket hög. Om endast någon av punkterna skulle ändra position skulle hela linjen kunna förändras från negativ lutning till positiv lutning.
Om vi hade haft många punkter, exempelvis 2000 stycken som visat r=-0,19 så hade vi haft en högre säkerhet och då hade vi kunnat säga att det finns viss korrelation, om än mycket svag sådan.
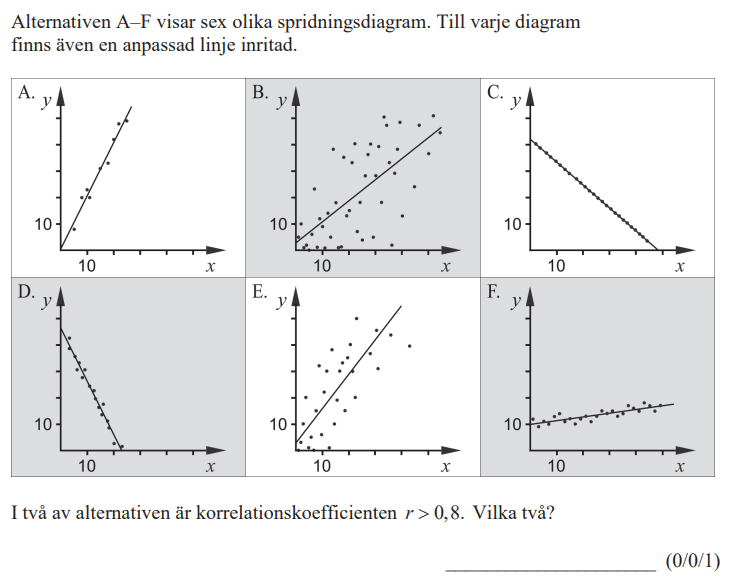
Uppgifter med videoförklaringar
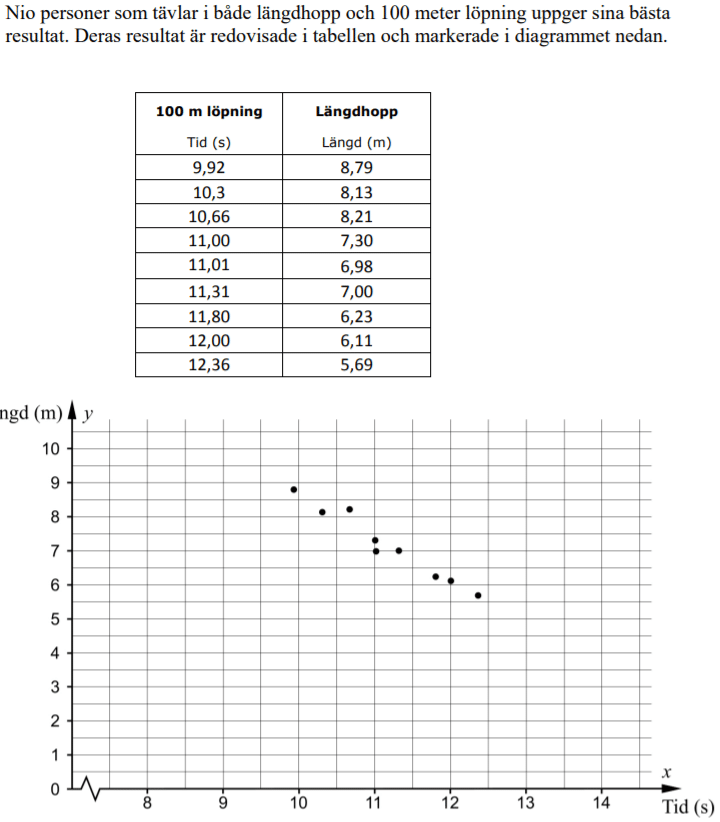
Löses utan digitala hjälpmedel. Från VT 2013 (Matematik 2a, 2b eller 2c).
Bedömningsanvisningar/facit (uppgift 13).
Löses utan digitala hjälpmedel. Från VT 2022 (Matematik 2b).
Bedömningsanvisningar/facit (uppgift 9).
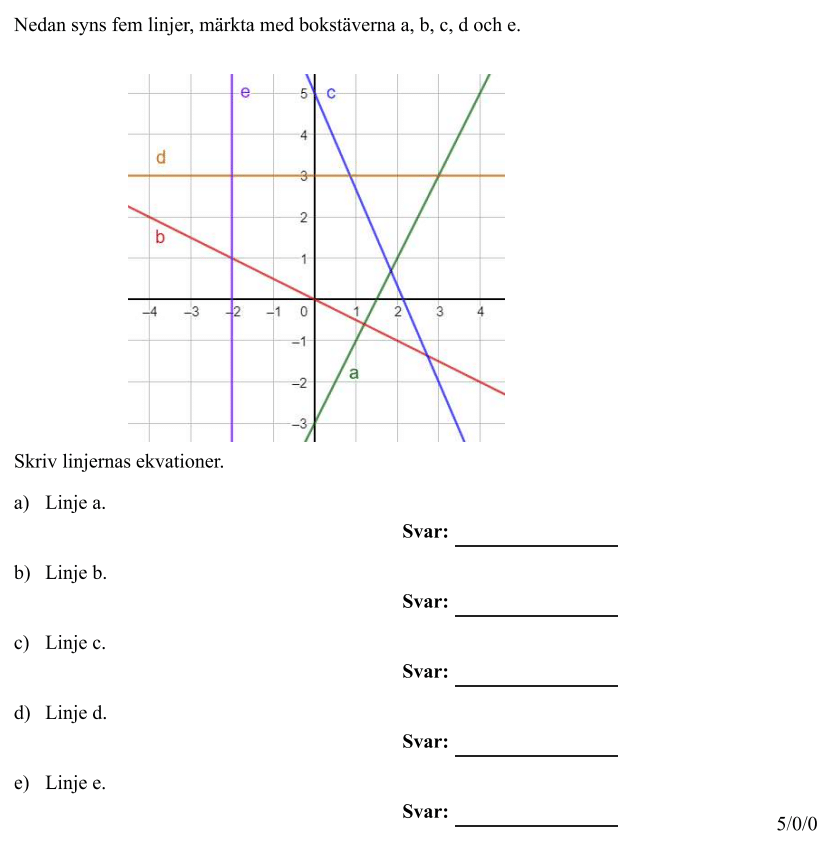
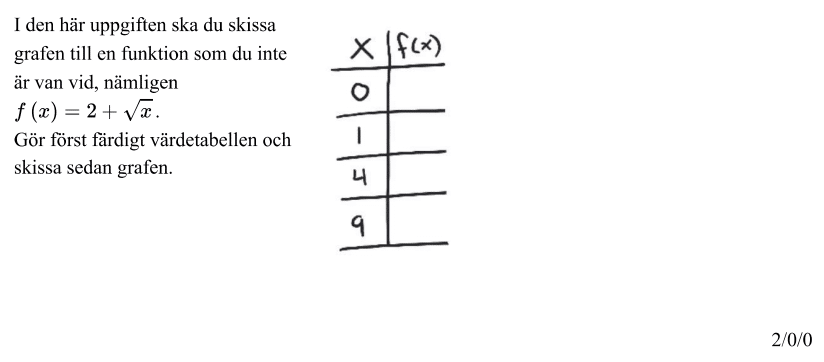
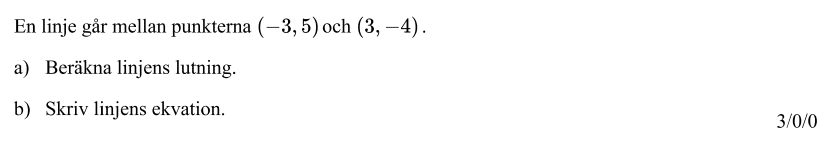
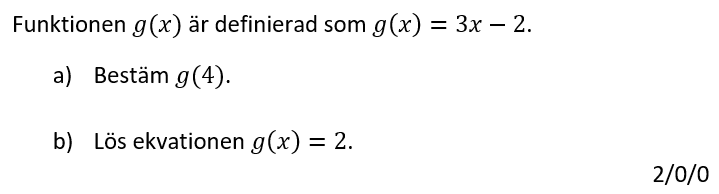
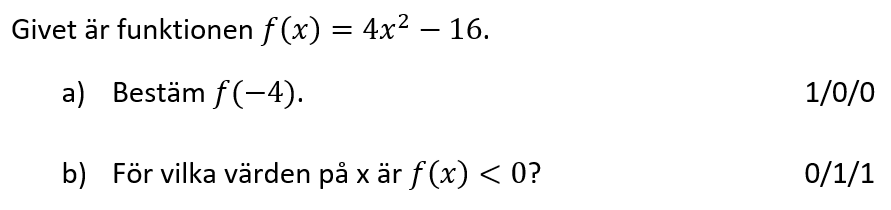
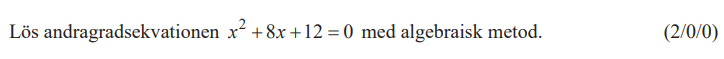
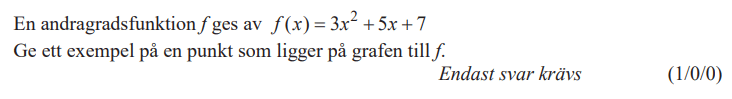
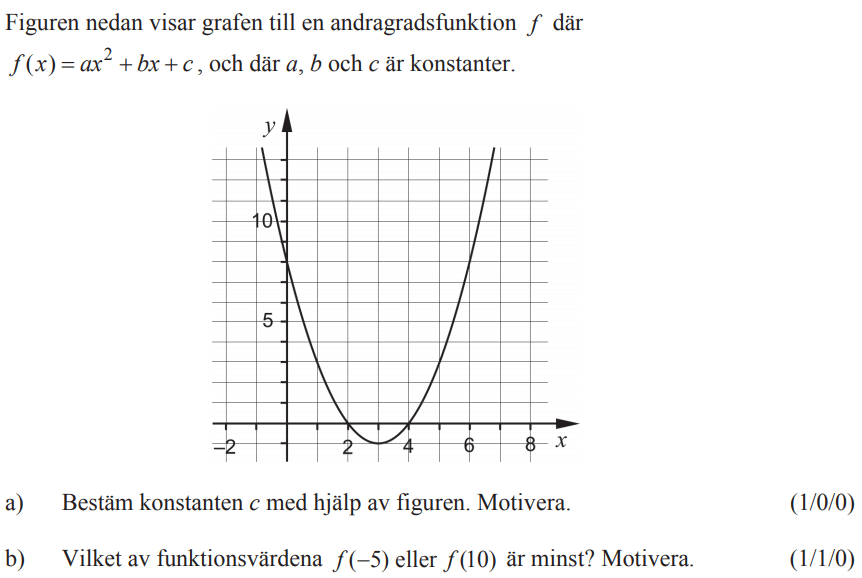
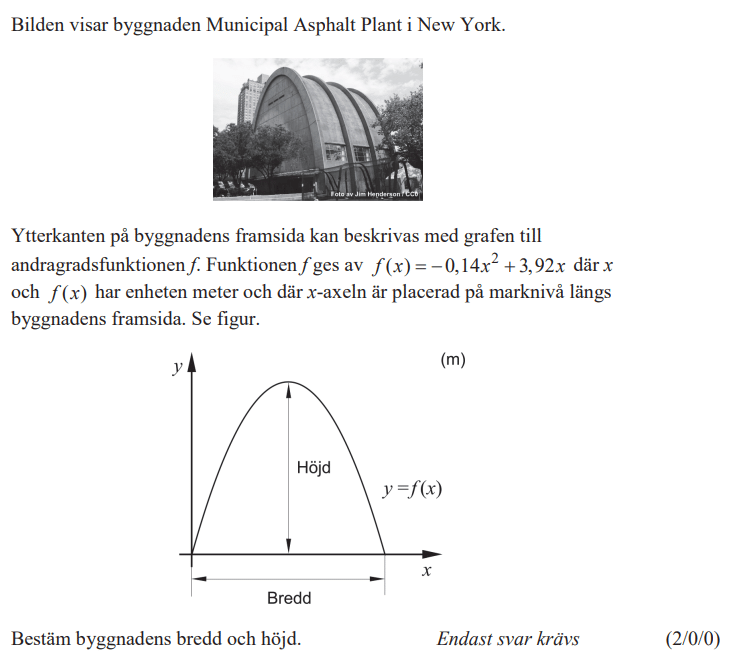
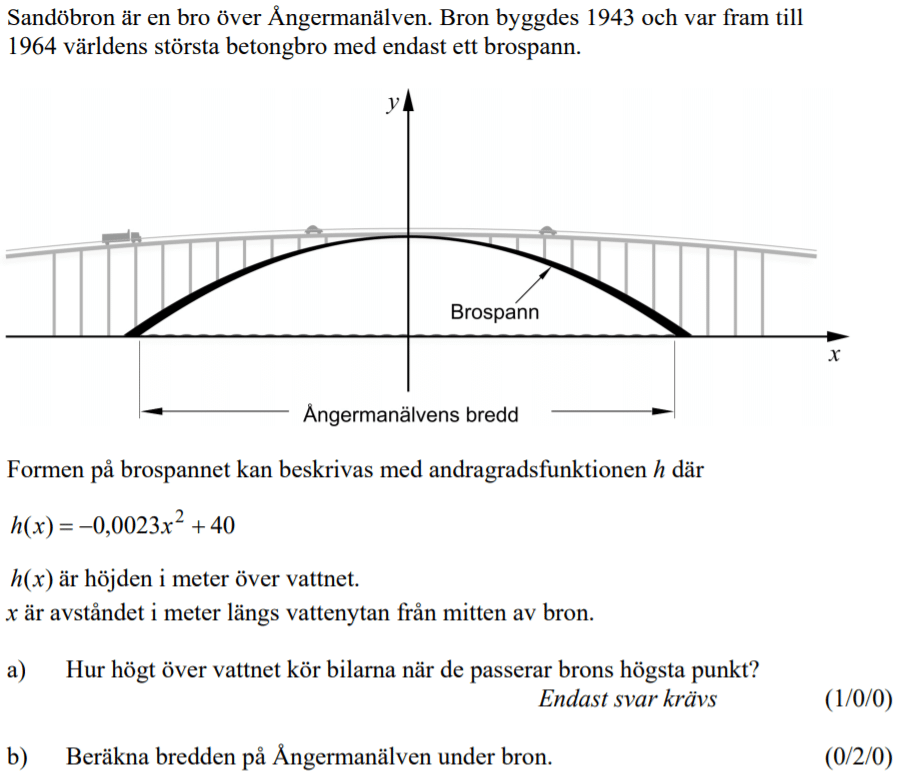
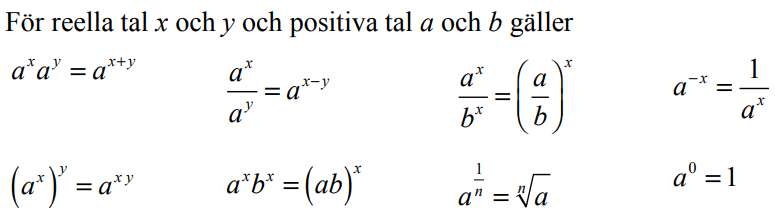
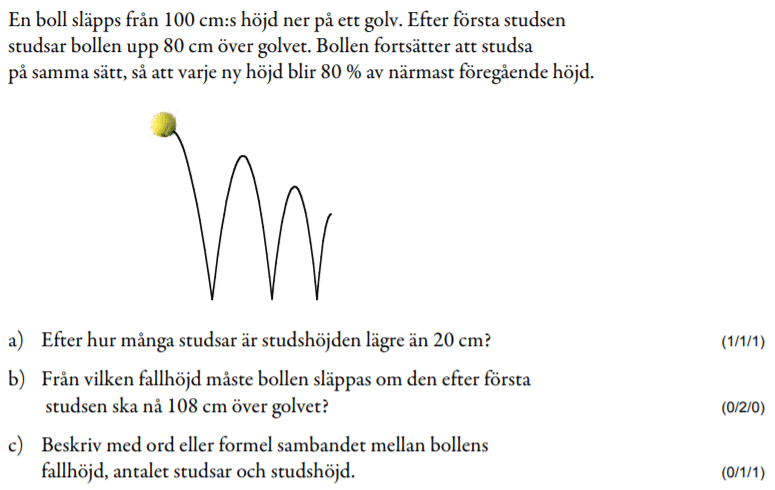
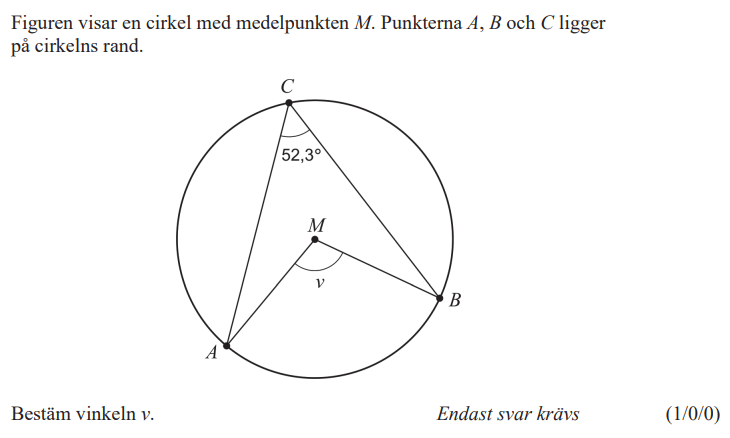
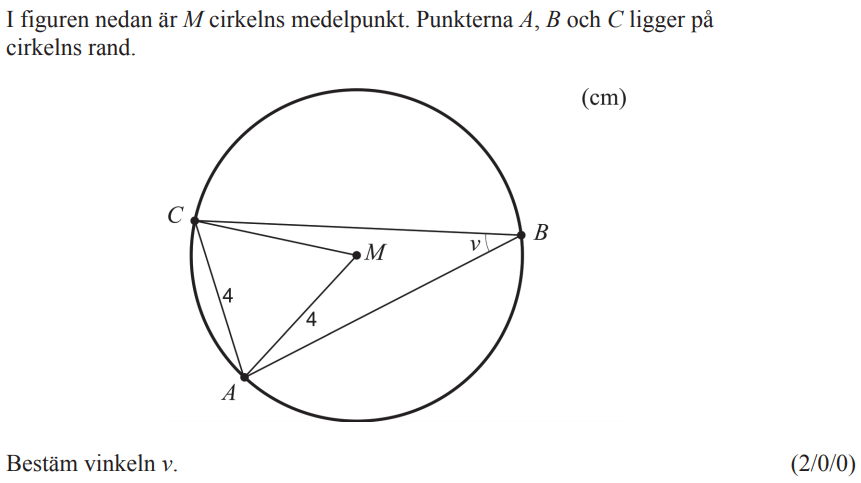
Fantastiskt! Precis vad många av mina elever behöver! Tack så mycket, Jonas!
Hej Dusan! Vad roligt att du tycker det! Jag jobbar vidare med att färdigställa detta, då och då när jag hinner. 🙂
du är bäst Jonas
tack vare dig kommer jag klara matten
Tack så mycket för allt arbete du lägger ned på detta och att du väljer att dela det helt öppet. Om mina elever frågar efter fler genomgångar förklaringar utöver det de får i klassrummet är vidma.se alltid mitt första tips till dem.
Extremt bra genomgång!
Jonas du är kung! Tack för din hjälp.